大展弦比机翼气动颤振的有限元分析

杨琼梁，史晓鸣，2，唐国安

(1.复旦大学 力学与工程科学系，上海 200433;2.上海机电工程研究所)

大展弦比机翼气动颤振的有限元分析

杨琼梁1，史晓鸣1，2，唐国安1

(1.复旦大学 力学与工程科学系，上海 200433;2.上海机电工程研究所)

在Theodorsen二元气动力的基础上，建立非定常气动力时域内积分形式的表达式或者等价的频域表达式，利用粘弹性结构振动分析中对积分方程的等价变换将其写成与结构动力学方程一致的二阶常微分方程，将气动力的影响作为对结构有限元模型质量阵、刚度阵和阻尼阵的补充，保留了结构原有的所有动力学特性，并且能够直接用计算结构动力学的通用有限元软件进行空气－结构耦合的整体动力学分析，适合应用于具有复杂结构的气弹问题。气动力模型的建立可以利用各种试验及数值方法得到的气动力数据，适用性强。算例给出了大展弦比机翼的颤振边界计算结果。

气动弹性;非定常气动力;颤振;有限元

气动弹性是研究弹性体与气动力之间相互作用的一门学科，是现代飞行器设计中的一个重要环节。其中，颤振是最引人关注的气动弹性动力学问题，颤振通常能导致飞行器结构的毁灭性破坏［1］。由于气弹分析中空气与弹性体相互耦合，而目前还没有一种分析工具能很好的对流体和弹性体两者同时进行分析计算，这也使得气弹分析变得较为复杂。

目前常见的气弹分析方法有:CFD/CSD耦合计算方法［2］和对气动力进行简化后的快速工程分析方法，例如基于当地流活塞理论的分析法［3－5］。其中 CFD/CSD耦合法计算精度较高，但是采用CFD计算非定常气动力时计算量大，且要在每个时间步内交换CFD和CSD两者的计算数据，造成整体的计算效率低;为了克服用CFD计算所带来的计算困难，实际应用中通常采用一些快速工程算法对非定常气动力计算做简化，如利用当地流活塞理论计算气动力，但活塞理论只在来流马赫数M∞≫1的情况下有较为满意的结果，计算范围有所限制。

在上世纪90年代，Silva提出将Volterra级数理论用于非线性非定常气动力的建模，建立起具有积分形式的气动力降阶模型，气动力计算精度高，并在一定程度上实现了气动力与结构的解耦［6－7］，但是积分形式的气动力不属于传统的结构激励载荷，从而造成计算复杂。本文的目的是在以积分形式表示的非定常气动力的基础上，在时域内将非定常气动力表示为与结构动力学方程一致的二阶常微分方程，从而将非定常气动力对结构的影响表示为对结构的附加质量、刚度和阻尼，并以此为依据在物理坐标下直接对结构进行修改，实现气动力与结构的解耦，在保留结构完整的动力学特性的条件下，应用传统的通用有限元软件进行空气－结构耦合的整体动力学分析。

1 非定常气动力建模及气动力与结构耦合

有限元离散模型表示的弹性机翼在非定常气动力作用下的振动方程为:

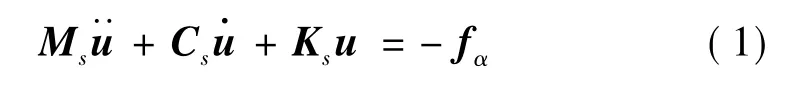
其中u为结构振动的节点位移向量;Ms，Cs和Ks为结构的质量、阻尼和刚度矩阵;－fα为作用在结构上的非定常气动力，通常可以表示为结构位移、速度和加速度的函数。

Fung［8］给出了机翼在不可压缩流中积分形式的升力系数和力矩系数，将气动力表示为:

其中Ma，Ca，Ka，Vp和Ap为相关的气动力参数。利用降阶法［9］可以通过各种气动力计算方法或者试验得到频域内的气动力数据点，并拟合成有理多项式，经过Laplace变化就能得到如(2)所示的非定常气动力表达式。

将非定常气动力式(2)代入式(1)，得到结构与气动力的耦合方程:

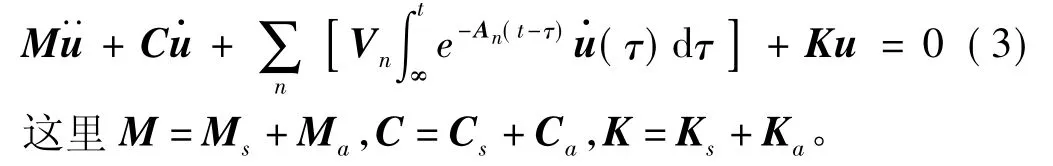
高淑华［10］在分析粘弹性结构振动时，证明了方程(3)表示的微分－积分型动力学方程可以等价地变换成纯微分型方程:

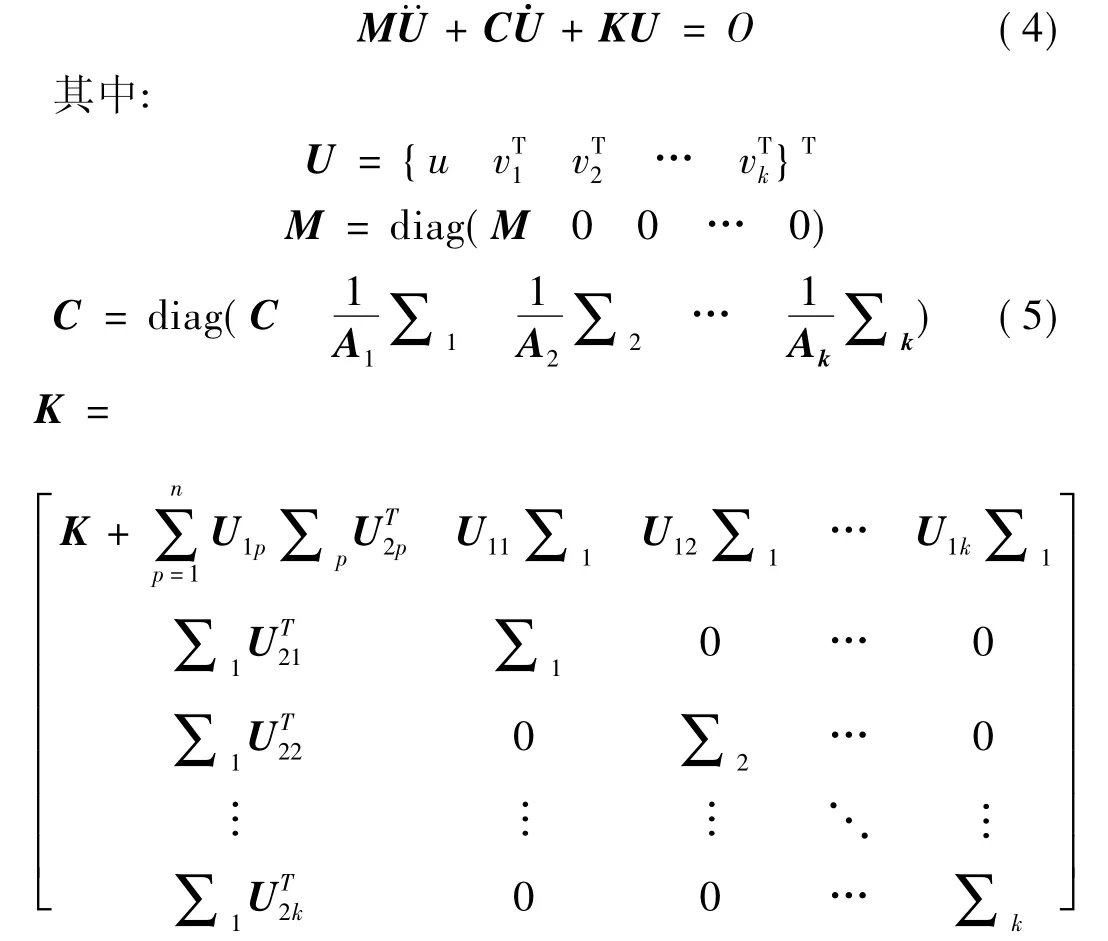
其中U1i、∑i等是矩阵Vp(p=1，…，k)的奇异值分解Vp=U1p∑pU2p。

周文博［11］利用这种等价变换的方法，分析了带有控制面的三元机翼颤振问题。证实了通过等价变换、可以利用通用有限元结构分析程序实现气动弹性耦合的颤振计算。但文献［11］仅仅考虑了简单的机翼模型，机翼是用弹簧和扭簧连接的二自由度刚体，控制面为由扭簧连接到机翼的单自由度刚体。这种模型简化较大，与实际弹性机翼存在很大差异。

2 大展弦比三维弹性机翼与气动力耦合模型

用 弹性平板有限元模型表示大展弦比三维弹性机翼，如图1所示。 气 弹计算将采用MSC.Nastran有限元程序，平板表示为80个CQUAD单元、节点数为99。

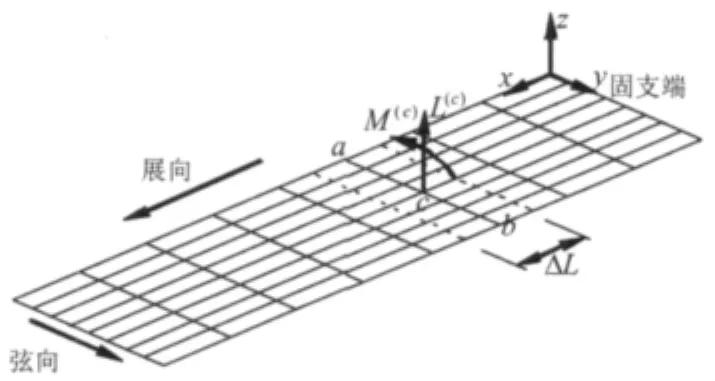
图1 大展弦比弹性机翼模型Fig.1 Model of the high-aspect ratio elastic wing

考虑到大展弦比机翼，机翼片条ab的弦向弹性弯曲可以忽略不计、弦向变形视为刚性，即直线ab变形后仍近似保持直线，其变形可以由某个节点的z向位移w(c)和绕x轴转角θ(c)z来表示。作用在整个机翼上的气动力可以近似地认为是由一系列作用在机翼片条上的气动力的累加，而片条上连续分布的气动力又可以简化为作用在节点c上的一对集中力(升力)L(c)和集中力矩M(c)。

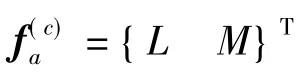
其中ΔL(c)为片条长度，系数见附录。

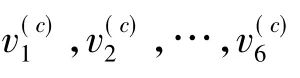
3 大展弦比均匀直机翼颤振实例计算

根据片条理论将直机翼沿展向分为10块，利用上述方法通过改变飞行速度V，得到每一块的气动力附加矩阵。由于=0，即气动力和力矩的作用点取在翼面中点，利用上述得到的气动力附加矩阵修改该点的质量、刚度、阻尼，最后用有限元分析程序(MSC.Nastran)的复特征值分析功能，计算空气－结构耦合情况下的复特征值，以特征值实部穿越零点作为依据来计算得到机翼的颤振边界。文献［12］中，将机翼近似为梁。计算结果表明第三阶振型发生颤振，相应的复特征值频率的实部变化如图2所示。本文计算所得到的颤振结果基本与文献结果如表2所示，误差小于6%，由于对气动力拟合时会引起一定误差，增加拟合阶数将有助于提高计算精度。

表1 大展弦比机翼参数Tab.1 Parameter of high －aspect ratio wing

表2 临界颤振速度与频率Tab.2 Critical flutter speed and frequency

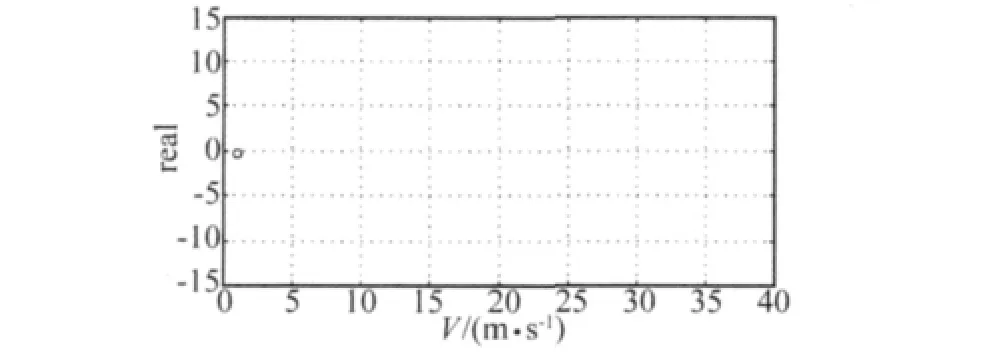
图2 第三阶频率实部Fig.2 Real part of the third mode

4 结论分析

利用粘弹性结构振动分析中对积分方程的等价变换方法，推导了积分形式的非定常气动力与结构动力学方程耦合的气动弹性分析方法，并以大展弦比直机翼有限元模行为算例，计算得到了其颤振频率和颤振速度，验证了方法的可行性。

将气动力作为对有限元中结构质量阵、刚度阵和阻尼阵的补充，完整保留了结构原有的动力学特性，避免了模态降阶带来的误差。对复杂结构具有较高的适应性，不仅可以用于计算平板单元的颤振，对其它各类有限元单元，如杆系、壳体等单元同样适用。直接利用有限元软件进行颤振分析，计算效率高。

文中的气动力模型来自于Theodorsen理论，但方法同样适用于以一阶Volterra级数表示的气动力降阶模型。只要通过CFD全流场计算或者试验流场分析等手段得到气动力的卷积表达式，就能对复杂结构进行气动－弹性耦合计算，具有很好的工程适用性。

［1］Dowell E H，Clark R，Cox D，et al.A Mordern Course in Aeroelasticity［M］.New York:Kluwer Academic Publishers，2004:1－5.

［2］ Chen X Y，Zhan G C，Hu Z J.Numerical Simulation of Flow Induced Vibration Based on Fully Couple Fluid-Structual Interactions［R］.AIAA-2004 －2240.

［3］杨炳渊，宋伟力.用当地流活塞理论计算大功角翼面超音速颤振［J］.振动与冲击，1995，14(2):60－63.

［4］杨炳渊，宋伟力.前缘激波脱体的大迎角翼面颤振工程计算方法［J］.振动与冲击，2002，21(4):100－103.

［5］Zhang W W，Ye Z Y，Zhang C A.Supersonic Flutter Analysis Based on a Local Piston Theory［J］.AIAA，2009，47(10)，2321－2328.

［6］张伟伟，叶正寅.基于非定常气动力辨识技术的气动弹性数值模拟［J］.航空学报，2006，27(4):579－584.

［7］张伟伟，叶正寅.基于CFD的气动力建模及其在气动弹性中的应用［J］.力学进展，2008，38(1):77－86.

［8］Fung Y C.An Introduction to the Theory of Aeroelasticity［M］.New York，John Wiley＆ Sons，Inc，1955.

［9］Piergiovanni M，Liviu L，Walter A.S.Volterra Series Approach for Nonlinear Aeroelastic Response of 2-D Lifting Surfaces［R］.AIAA －2001－1459.

［10］高淑华，赵 阳，等.粘弹性结构动力学分析的等效粘性阻尼算法［J］.振动与冲击，2005，24(1):18－21.

［11］周文博，陈力奋，杨琼梁，等.基于结构动力学方法的气动弹性分析［J］.振动与冲击，2011，30(4):135－138.

［12］赵永辉.气动弹性力学与控制［M］.北京:科学出版社，2007，134－135.

附录

式(6)中的系数

Flutter analysis for a high-aspect ratio wing with finite element method

YANG Qiong-liang1，SHI Xiao-ming1，2，TANG Guo-an1

(1.Department of Mechanics and Engineering Science，Fudan University，Shanghai 200433，China;2.Shanghai Electro-Mechanical Engineering Institute)

Expressions for unsteady aerodynamics in time domain or frequency domain were established based on Theodorsen theory.The expressions with integration were converted into second order ordinary differential equations.The effects of unsteady aerodynamic force on a structure were regarded as comlements of mass matrix，stiffness one and damping one of finite element model of a structure.The whole dynamic characteristics were retained.General finite element software could be used to calculate the flutter boundary of an air-structure coupled model.The method was suitable for solving aeroelastic problems of complex structures.The unsteady aerodynamic data obtained with any numerical method or test could be used to establish an unsteady aerodynamic model.The proposed method was applicable to different cases.The flutter boundary of a high-aspect ratio wing was calculated.

aeroelasticity;unsteady aerodynamics;flutter;finite element method

V211.47

A

国家自然科学基金资助项目(90716001)

2010－05－21 修改稿收到日期:2010－08－20

杨琼梁 男，博士生，1984年7月生

唐国安 男，教授，1962年生