电动力绳索系统的周期解求解及其稳定性分析

张 勇

(1.西安铁路局，西安 710015;2.兰州交通大学 机电技术研究所，兰州 730070)

电动力绳索系统的周期解求解及其稳定性分析

张 勇1，2

(1.西安铁路局，西安 710015;2.兰州交通大学 机电技术研究所，兰州 730070)

对运行在倾斜圆轨道上的电动力绳索系统的动力学特性进行了分析研究。首先建立了系统的动力学模型，分别采用摄动法及推广后的数值算法求得系统的基本周期解，并运用所给数值算法中的稳定性判据分析了周期解的稳定性，得出该系统周期运动不稳定的结论。最后进行仿真验证，结果表明在摄动量较小时，两种求解算法得到的周期解基本相同，但当摄动量较大时，摄动法求得的周期解发生了畸变，不理想此时通常借助数值算法加以求解;仿真结果同样证实了所得周期解的不稳定特性。

电动力绳索系统;周期运动;周期解求解;稳定性分析

绳系卫星系统(简称TSS)是指用一根细长柔软的绳索连接起来的双星(母星与子星)系统。近年来TSS已经成为航天领域的一个研究热点，国内外学者做了大量的研究，并相继投入试验中。其中电动力绳索系统(当TSS的绳索导电时，简称EDT)的研究成为目前最活跃的一个分支。该系统不仅可用于大气层测量等各种实验，还可以将负载送入新轨道或卫星回收，以及空间站的机动等。TSS在倾斜圆轨道上运行时，若绳索中不通电流，系统将稳定在当地的垂线方向。若系统中通过电流，这种平衡位置消失，代之出现周期运动。前者的研究已经较为成熟，相比之下后者的研究还较欠缺，国内外学者做了一些初步的探讨，结果表明当受到电动力影响时，系统的动力学行为相当丰富，会出现一些复杂的周期运动，在没有外加控制的情况下，这种周期运动是不稳定的，不稳定源于非线性共振带给系统的持续能量泵入［1，2］。

对ETD系统复杂动力学分析的程度取决于周期解求解算法的有效性，随着研究的不断深入，一些周期解求解算法相继引入到该系统中，归纳起来可分为解析法与数值法两大类。文献［3］利用摄动法在摄动量较小的情况下求得了系统的周期解。文献［4］给出了一种周期解的数值求解算法——预测校正法，算法每迭代一次需要完成预测与校正两大步，计算量较大。文献［5］给出了一种单自由度系统周期解的求解算法及其相应的稳定性判据，该算法实现起来比较容易。文中将该算法加以推广，并应用到两自由度系统中，得到理想的结果。

本文首先建立并简化了电动力绳索系统的动力学模型，分别利用摄动法与数值法求得了系统的周期解，并利用文中所给数值算法中的稳定性判据加以理论分析，得出系统周期运动不稳定的结论。最后在Matlab中进行仿真验证，结果表明，摄动量较小时，两种方法求得的周期解基本相同，但当摄动量较大时，摄动法求得的周期解发生畸变，结果不够理，此时通常借助数值算法求解。本文所给出的数值算法成功地求得了系统的周期解，弥补了摄动量较大时摄动法求解的不足，并且也克服了文献［4］中的数值算法在求解系统周期解时计算量较大的困难。仿真结果同样证实了系统周期运动的不稳定特性，即从任一周期解附近开始的运动，经过若干周期后完全发散直至失稳，为后续的控制工作奠定了基础，也为以后电动力绳索系统的成功试验提供了一定理论依据。

1 电动力绳索系统建模

为了更有效地研究电动力绳索系统受到电磁力影响时所表现出的复杂周期运动及其不稳定特性，在建立EDT模型时，做如下的假设:

① 假设地球是中心引力场，除地球中心引力和绳索电动力外，不考虑其它的干扰力;② 母星的质量远远大于绳索和子星的质量;③ 地球磁场为非倾斜偶极子模型，其磁场强度在绳索的长度方向上均匀分布;④母星被限制在圆轨道上，做开普勒运动;⑤ 绳索中电流恒定。

建立如下的三套右手直角坐标系:① 地心惯性坐标系OEXYZ，其中:OE为地球质心，OEX指向第一个升交点，OEZ沿地球自转轴，OEY与其他两轴构成右手坐标系。② 轨道坐标系oxyz，其中:o为母星质心，ox沿当地垂线方向指向天顶，oz垂直于轨道平面，oy与其他两轴构成右手坐标系。③ 体坐标系Ox1y1z1，ox1固联在绳索上(见图1)，θ为绳索的面内摆角，φ为绳索的面外摆角(见图2)。

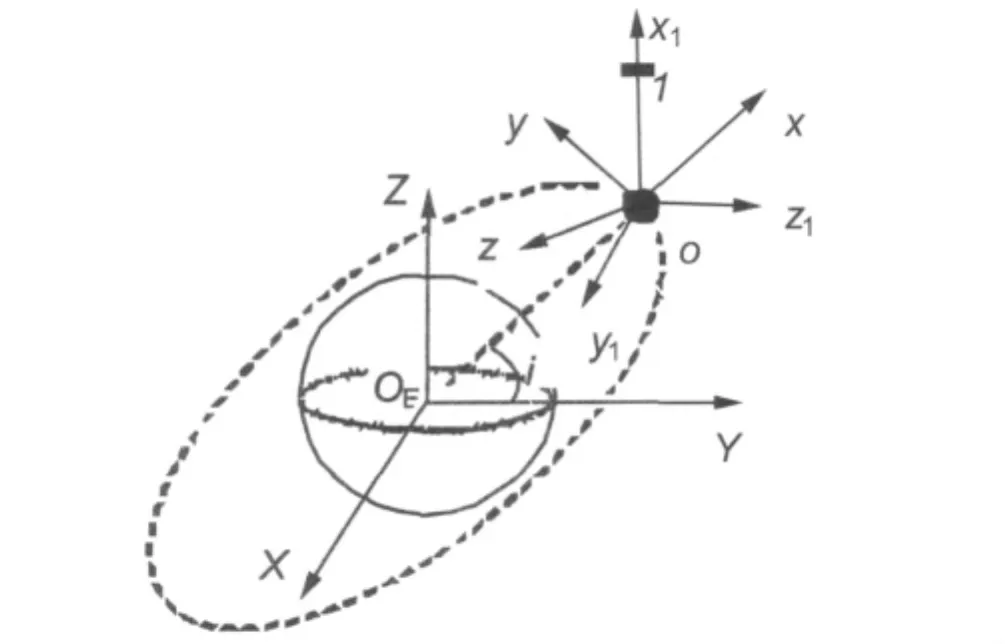
图1 电动力绳索系统的坐标系Fig.1 Coordinate frames of Electrodynamic Tether system

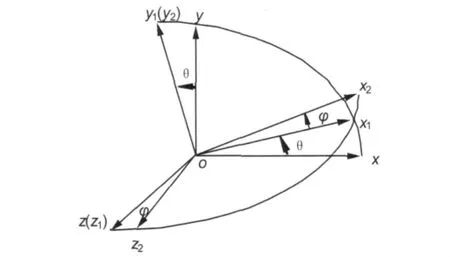
图2 轨道坐标系与体坐标系的转换关系Fig.2 Transformation from orbital coordinate frame to body coordinate frame

在没有施加控制的情况下，系统只受重力梯力矩与电磁力矩的作用，利用欧拉角的转换关系与拉格朗日方法，得到系统的无量纲动力学方程:

绳索矢量与地磁场矢量在轨道坐标系中表示为

对于一个绝缘的系绳(即ε=0)，方程组(3)存在奇点，解为平衡点，对应的位置(θ=φ=0)是系统的稳定位置，这种情况在文章［7］中已得到证实。但是，当系绳导电(即ε≠0)时，方程组(3)的平衡点消失，出现2π周期解［1］，在没有外加控制的情况下，这种周期解不稳定。下面针对这种情况做详细研究，分别采用解析法与数值法求取系统的周期解，并判断其稳定性，最后进行仿真验证。

2 EDT周期解求解及其稳定性分析

当绳索中有电流流过(ε≠0)时，系统的平衡位置(θ=φ=0)不再出现，代之表现为周期运动，周期大小取决于强迫项的周期值，也就是本文中的轨道周期值T=2π/ω，幅值取决于ε、i值的大小。然而获得周期解是相当困难的，通常借助数值计算才能得到。当摄动量ε较小时，也可以通过摄动法求得周期解。

2.1 摄动法求解周期解

首先假设系统的周期解为x(ν，ε)，然后展开成ε的幂级数形式:

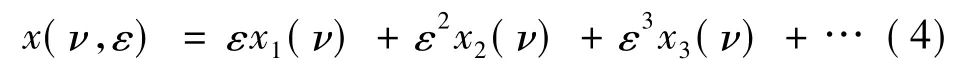
将上式代入到方程组(3)中，得到下面一系列的微分方程组:

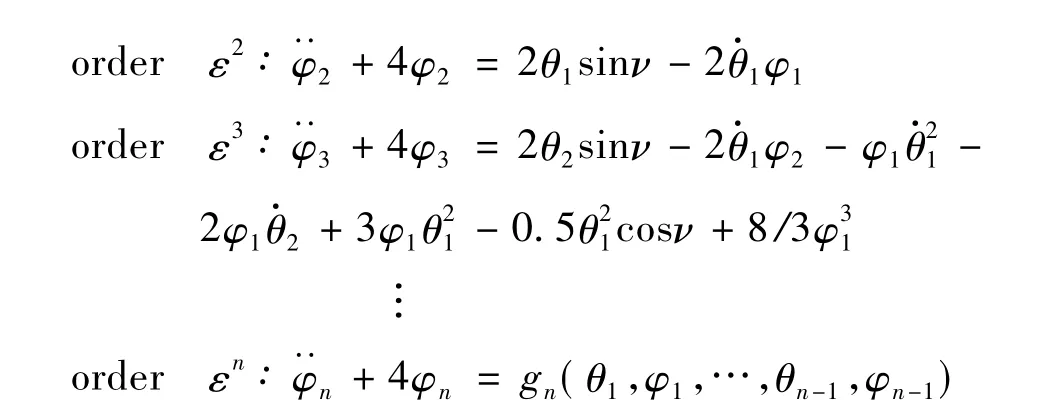
在Matlab符号求解器的帮助下，由上述方程组的第一式解得派生系统的解，依次带入下一式求出各阶近似解，最后代回式(4)后得到原系统的周期解:

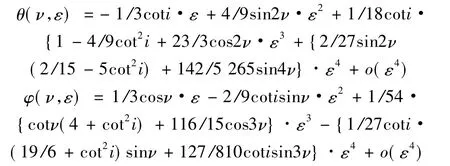
2.2 数值法求解周期解及其稳定性分析

当摄动量ε较小时，用摄动法求得的周期解跟数值方法得到的周期解基本相同，但当ε较大时，用摄动法求的周期解不理想，此时一般通过数值方法求系统的周期解［4，8］。文献［5］给出了一种单自由度系统周期解的迭代算法及其稳定性判据，将该算法推广应用到本文的两自由度系统中，具体步骤如下:

方程(5)中有两个可变参数，分别固定其中一个参数，改变另一个，求得对应的周期轨道族。

假设先固定i值，将ε看作变化量，则求解周期解的迭代算法可归纳为:在k步上假设ε=ε(k)，方程(4)近似解为X=X(k);改变ε，在第k+1步中令ε(k+1)=ε(k)+Δε(k+1)，设此时的解为 X(k+1)=X(k)+ΔX(k+1)，带入式(4)得:

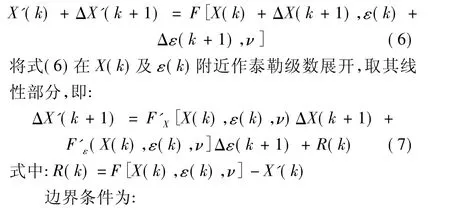
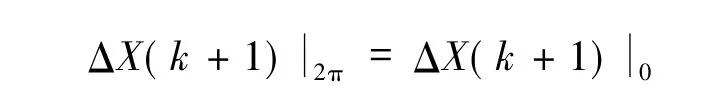
F'X、F'ε是具有周期时变系数的雅克比矩阵。式(7)是求解(4)的周期解的基本迭代关系式。若步长Δε(k)取很小时，可以得到很高的求解精度。作为迭代算法的第一步，取ε(1)=0。

式(6)是非线性齐次微分方程，其解由两部分组成:ΔX(k+1)=yk+1+αYk+1。各部分解由下面相应的同伦方程求得，并且给出了所求周期解的稳定性判据，具体如下:

同样，固定ε值，将i看作变化量，采用上述算法求得对应的基本周期轨道族。最后运用上述稳定性判据分析系统周期解的稳定性，结果表明所有的解都不稳定，下面的仿真结果也证实了这一特点。

3 仿真及结果分析

下面是分别采用上述摄动法与数值算法得到的若干参数下的系统基本周期解族图及某任意一周期解表现出的不稳定特性图。

图3是采用摄动法求得的周期解，图中系统参数取值为轨道倾角 i=40°，摄动量 ε =0.1、0.2、0.3、0.4、0.5、0.7。图4、图5是采用数值算法得到的周期解族，其中图 4 取值为 i=40°，ε =0.1、0.2、0.3、0.4、0.5、0.7;图 5 取值为 ε =1，i=20°、25°、30°、35°、40°。

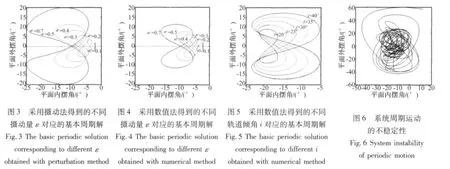
对比图3、图4可知，在摄动量ε较小(对应图中ε =0.1、0.2、0.3、0.4)时，摄动法求得的周期解与数值计算得到的结果基本相同，但当摄动量ε较大(对应图中 ε=0.5、0.7)时，两种算法得到结果相差甚大，此时摄动法失效，通常用数值法获得周期解。从图4、图5中还可以看出，不同轨道倾角i、摄动量ε分别对应不同的周期解，随着两参数值的增大，所得周期解的幅值也相应地增大，即周期运动的幅度加大，不稳定性程度同样加大。根据算法中给出的稳定性判据可知所有求得的周期解都不稳定，图6是其中任意一个周期解(取值ε=1，i=40°)受到初始扰动后所表现出的不稳定特性，可以看出，即使系统受到一个很小的初始扰动，也就是从离目标轨道很近的点开始的运动，经过若干个轨道周期后，同样完全偏离目标轨道直至失稳。

4 结论

本文对运行在倾斜圆轨道上的电动力绳索系统的动力学特性进行了分析研究，建立了系统的动力学方程，引入了一种新的周期解求解算法，并与摄动法求得的结果进行比较，结果表明在摄动量较大的情况下，文中给出的数值算法在求解周期解时具有很大的优越性。最后理论分析了所得周期解的稳定性，结果表明系统的周期运动是不稳定的，该研究结果进一步揭示了受到电磁力影响的电动力绳索系统与不受电磁力的常规绳系卫星系统动力学特性的不同，电动力绳索系统周期运动固有的不稳定性为后续的控制工作提出了要求，也为以后电动力绳索系统的成功试验提供了一定理论依据。

［1］ Inarrea M，Pel ez J.Libration control of electrodynamic tethers using the extended time-delayed autos-ynchronization method［J］.Journal of Guidance，control，and Dynamics，2010，33(3):923－930.

［2］ Peláez J，Lorenzini E C.Libration control of electrodynamic tethers in inclined orbits［J］.Journal of guidance，control，and dynamics，2005，28:269 －279.

［3］ Peláez J，Lorenzini E C，et al.A new kind of dynamic instability in electrodynamic tethers［C］. Space flight mechanics 2000，Advances in the Astronautical Sciences，2000:449－476.

［4］ Peláez J，Lara M.Periodic solution electrodynamic tethers on inclined orbits［C］. Journalofguidance，control，and dynamics，2003，26(3):395 －406.

［5］于绍华.绳系卫星中的周期运动［J］.宇航学报，1997，18(3):51－58.

［6］李德信，徐健学.求解非线性系统周期轨道及其周期的一种方法［J］.机械强度，2002，24(1):35－38.

［7］ Sun Q G，Van der Heijden G.A model for a 3D spinning rigid electro-dynamic tether［C］.Proc-eedings of international conferenceon nonlinearmechanics，Shanghai: Shanghai University，2007:672 －678.

［8］ Inarrea M.Chaos and its control in the pitch motion of an asymmetric magnetic spacecraft in polar elliptic orbit［M］.Chaos

，

solitons ＆ fractals.2007.

Periodic solutions and stability analysis for a electrodynamic tethered system

ZHANG Yong1，2

(1.Xi'an Railway Bureau，Xi'an 710015，China;2.Mechachonics T＆R institute，Lanzhou Jiaotong University，Lanzhou 730070，China)

Dynamic behavior of a electrodynamic tethered system operating in a circular inclined orbit was studied.The dynamic model of the system was described，the basic periodic solution was obtained using perturbation method and a new numerical method.The stability of the periodic solution was analyzed based on the stability criterion in the numerical algorithm and it was concluded that the system periodic motion is instable.Finally，two algorithms were compared with simulation.The results showed that the periodic solutions obtained with the two algorithms are the same basically when perturbation is smaller，but the periodic solutions obtained with perturbation method are distorted when perturbation is large，at this time the numerical algorithm is normally adopted;instability of the periodic solutions is also confirmed with the simulation results.

electrodynamic tethered system;periodic motion;periodic solution;stability analysis

V412.4

A

英国皇家学会王宽诚教育基金资助项目《Stability of Electrodynamic Space Tethers》(LJCina/2005R1);中英高校科研合作项目(CHINA-UK SCIENCE NETWORKS)《Control of Electro-dynamic Space Tethers》

2009－07－24 修改稿收到日期:2010－03－22

作 者 张 勇 男，硕士生，1984年生