时滞速度反馈对软弹簧Duffing系统安全盆的控制研究

尚慧琳

(上海应用技术学院 机械工程学院，上海 200235)

时滞速度反馈对软弹簧Duffing系统安全盆的控制研究

尚慧琳

(上海应用技术学院 机械工程学院，上海 200235)

为了利用时滞反馈对于非线性系统实施安全盆侵蚀控制，以一个软弹簧Duffing系统为例，对系统引入线性时滞速度反馈，研究时滞速度反馈对系统安全盆侵蚀的控制作用。首先通过Melnikov函数法分析时滞受控系统的安全盆的边界分形条件;再以时间滞后量为变参数，通过四阶龙格－库塔法和蒙特－卡罗方法，刻画安全盆形态，计算安全盆面积。发现时滞速度反馈对影响安全盆边界有着重要作用，通过增大时滞量，可以对系统的安全盆侵蚀进行有效抑制。该研究结果说明时滞速度反馈是控制系统的安全盆侵蚀的有效手段。

软弹簧duffing振子;安全盆侵蚀;时滞;反馈增益;分形

质点的运动振幅超过一定限度，往往会导致结构的破坏和工程故障如船舶倾覆［1］，电网崩溃［2］等，由此产生了振动的有界性问题，也引起了对非线性系统的安全盆(safe basin)的研究。以英国学者Thompson［3］为首的科学家首先提出了安全盆的概念。系统的安全盆被定义为所有有界解吸引盆的合集。如果安全盆具有分形边界［4］，那么系统初始条件稍有改变，从原无侵蚀的安全盆的内部出发的轨线将可能逃逸出此安全盆，从而导致系统运动无界而引起系统崩溃，这种现象被称为安全盆的侵蚀(erosion of safe basins)［5－7］。安全盆的侵蚀往往触发工程结构的破坏，因此从应用的观点出发，有必要对系统安全盆侵蚀现象进行研究并有效控制。

多年来，关于非线性系统安全盆的研究已经取得了一定进展。如 Thompson［1，3］研究了船舶激励为规则波时系统的安全盆，发现激励振幅的增大会引起安全盆的侵蚀。甘春标等人［5］研究了软弹簧杜芬振子中参数的非定常变化对系统安全盆侵蚀的影响，指出外激励的高频作用可以有效降低安全盆的侵蚀。徐鉴等人［6］研究了具有三次非线性的Duffing－Mathieu型系统在主参数共振下安全盆侵蚀和控制，发现主参数共振情况下，增大阻尼可以抑制安全盆侵蚀，而参振激励下振幅的增大却加速安全盆的侵蚀;时变激励下振幅的改变则可以有效控制安全盆侵蚀的速度。系统参数的变化常常会引起安全盆的侵蚀［1－7］，因此，在应用中常常通过调整系统参数如增大阻尼、改变激励等被动控制方法来抑制安全盆的侵蚀，而极少采取主动控制方法。

本文对安全盆的侵蚀提出一种主动控制方法，即时滞速度反馈。这是因为研究表明［8－11］，时滞反馈是控制动力系统动力学行为的好方法，时滞能够引起系统失稳，出现多吸引子共存、概周期运动、混沌运动等复杂动力学行为。而多吸引子共存则为增大有界解吸引域的集合即安全盆提供了可能性。本文考虑一个典型的软弹簧Duffing振子，对系统施加线性时滞速度反馈，研究时滞反馈对系统安全盆侵蚀的控制。本文安排如下:第二节给出研究模型，并应用Melnikov函数法得出安全盆的边界分形条件;第三节给出时滞系统安全盆的定义，并在此基础上数值研究时滞量对系统安全盆边界和尺寸的影响规律。最后一节给出结论。

1 安全盆的边界分形条件

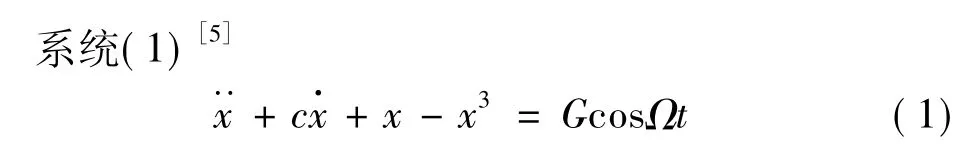
是一个典型的软弹簧Duffing振子，同时也可以作为刻画轮船在海面运动的有效模型［5，7，12］，用来描述船舶波浪中不考虑操舵的单自由度艏摇运动方程，其中x常常用来描述船舶的横摇角，当x过大时，船舶会发生横甩(即大幅艏摇运动)［7，12］，从而导致船舶倾覆。对系统(1)施加线性时滞速度反馈，得到

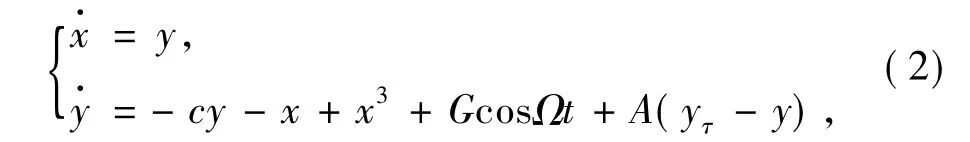
其中yτ=y(t－τ)，τ是时滞量，A是反馈增益系数。当τ=0时，系统(2)可以退化为系统(1)。方程(2)可以看成一个单通道反馈控制系统的数学模型，如图1所示.由图1知，时滞反馈在控制系统动力学行为方面扮演着重要角色。

图1 时滞反馈控制系统(2)简易框图Fig.1 Simplified diagram of the delayed feedback controlled system(2)

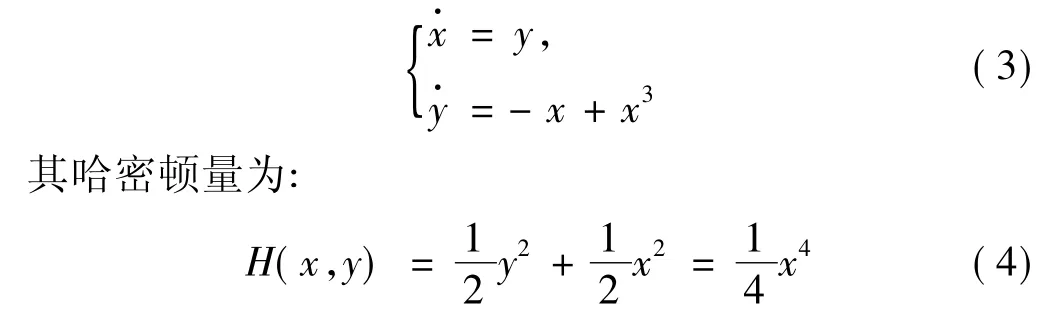
无扰动无时滞的软弹簧Duffing振子系统可写成:

因此，根据线性近似系统的特征值和(4)式可知，平衡点(0，0)为其中心，奇点(±1，0)为两个鞍点，且有两条异宿轨线:

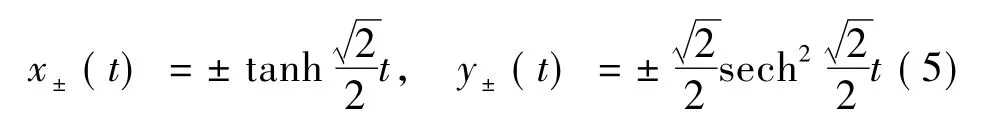
为了便于分析，将方程(1)和(2)中的变量进行重新标度

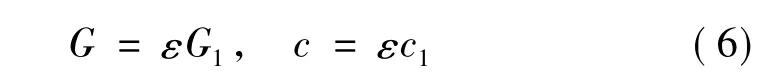
其中0＜ε≪1。则系统(1)相应的Melnikov函数为:

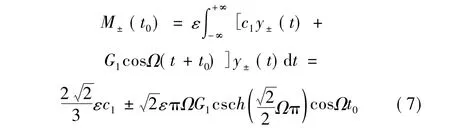
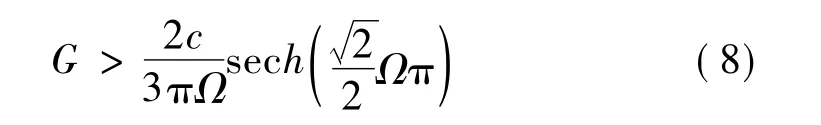
而对于施加时滞速度反馈之后的系统(2)，当反馈增益K和时滞量较小时，可以将时滞速度反馈项看成是扰动项，可设:

则受控系统(2)的Melnicov函数为:

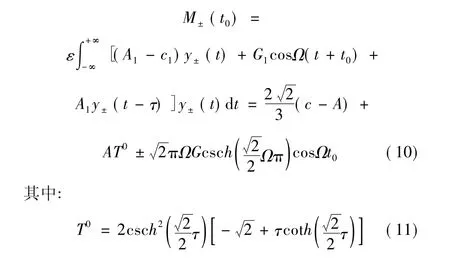
对于系统(1)，如果参数取值满足

因此只要选取适当的反馈增益项系数A和时滞量τ，使得:

则稳定流形和不稳定流形在Poincaré截面上不会横截相交，也就能够有效地抑制了安全盆边界的分形。

因此由理论分析可知，时滞速度反馈在一定条件下可以控制系统安全盆的侵蚀。而对于在无控制状态下已经被侵蚀的系统安全盆，时滞速度反馈对安全盆侵蚀的控制效果将在下一节通过数值模拟来体现。

2 安全盆侵蚀的控制效果

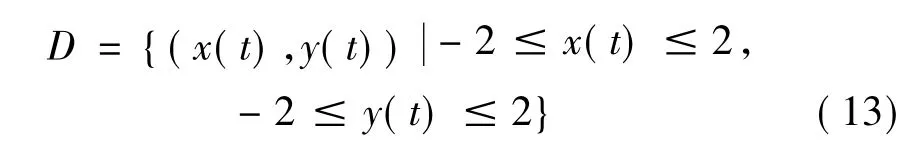
该区域包含了系统(1)的所有奇点和两条异宿轨线。当t=0时，本文在－2≤x(0)≤2这样一个初始值范围内运用四阶龙格－库塔法和点映射蒙特－卡罗方法来刻划安全盆，其中初始点的个数为640×240。即在初始轴x(0)方向将［－2，2］划分为639等份，由此产生640条平行于y(0)轴的格线;而在对应的y(0)方向将［－2，2］划分为239等份，产生240条相应的格线;平

2.1 时滞对于安全盆边界的影响

在常微分动力系统(ODE)中，安全盆常常被定义为所有有界解吸引盆的集合［1］，而无界解则对应导致破坏的危险振动。由于DDE系统初始条件与ODE系统完全不同，时滞微分动力系统的解往往由初始条件z(t)=z0(t=0)和 z(t)=φ(t)(－τ≤t＜0)共同决定，其中 z(t)=(z1(t)，z2(t)，…，zn(t))T，为系统状态变量。因此这样的初值吸引域很难直观地刻画与评价。然而，对于带时滞反馈的控制系统，由于在时滞反馈控制系统零时刻以前没有信号返回到系统，可以给定初始条件为z(t)=z0(t=0)和z(t)=0(－τ≤t＜0)。因此，我们定义时滞反馈控制系统的安全盆为零时刻状态空间z(0)上所有有界解吸引域的集合［5］。因此对于所研究的时滞速度反馈控制系统(2)，根据以上定义，系统安全盆应为位于零时刻状态平面x(0)－y(0)的所有有界解吸引域的集合。

本节选取一个充分大的有界区域D:行x(0)轴和平行于y(0)轴的格线相交，将产生640×240个格点，这些格点就是系统解的初始值。由于研究的是系统的长期动力学行为，则当系统响应在10 000个参数激励周期内如果仍未逃逸出有界区域D，认为此解是安全有界的，否则是不安全的。其中数值积分步长为1/4 000个激励周期。在安全盆图形中，白色区域对应有界解的吸引域，即安全盆，而黑色区域则对应逸出的无界解吸引域。对系统(2)，给定c=0.01，Ω=1和A=0.2，将时滞τ从0增大到2π。图2和图3分别表示G=0.1和G=0.3时系统(2)的安全盆随时滞的变化情况。

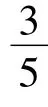
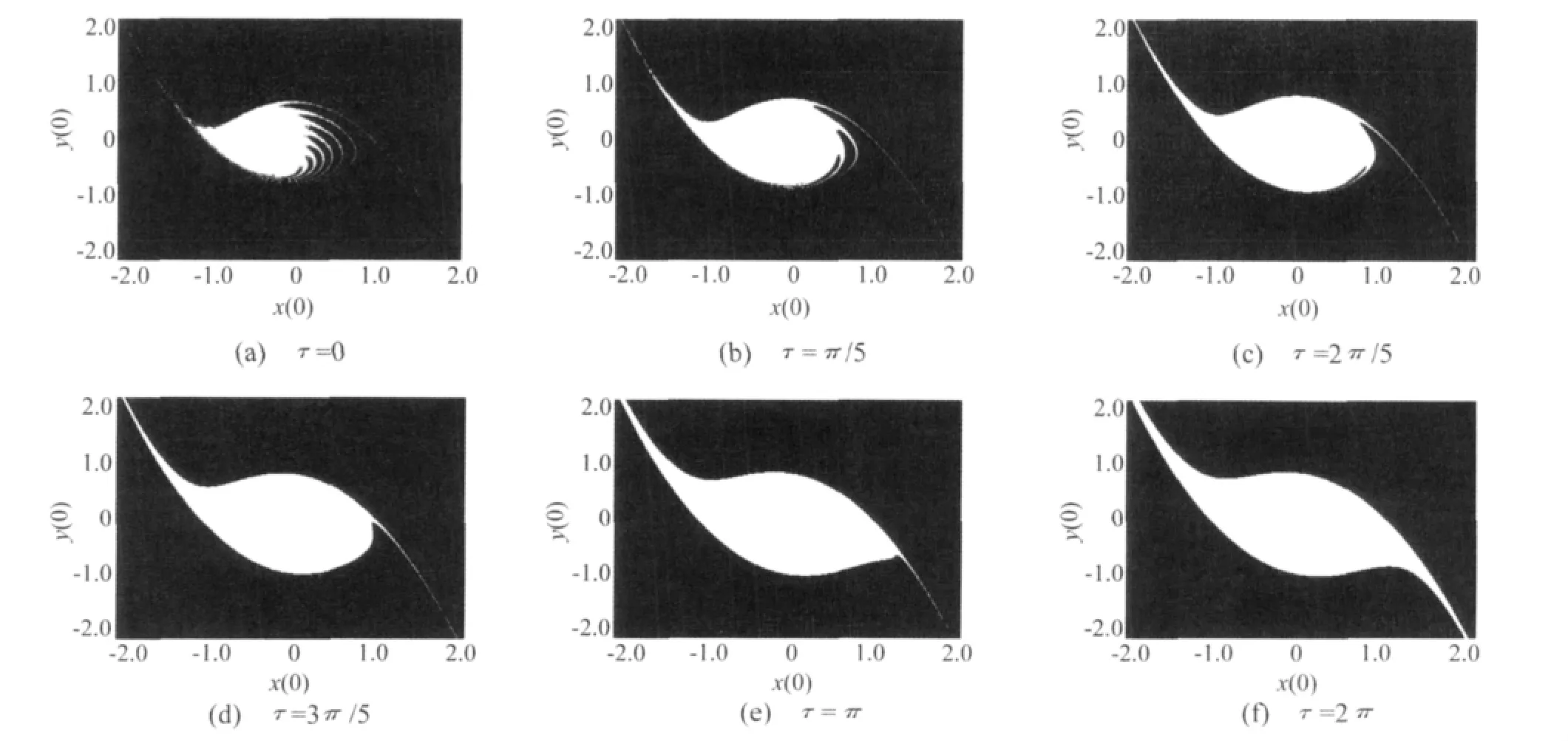
图2 G=0.1时系统(2)安全盆随时滞的变化图Fig.2 Evolution of the safe basin of system(2)as the delay increases when G=0.1

图3 当G=0.3时系统(2)的安全盆随时滞的变化图Fig.3 Evolution of the safe basin of system(2)as the delay increases when G=0.3

2.2 时滞对安全盆面积的影响

为了进一步图2和图3中出现的安全盆边界突然分形现象，如图4所示，考察安全盆面积即白色区域的面积随时滞量的变化，其中时滞的变化。根据式(8)可知，G=0时系统(1)的安全盆不会受到分形侵蚀。本文将边界光滑，没有受到分形侵蚀的系统(1)的安全盆称为“初始盆”(如图4)，定义其面积为 1 或 100%［10］。因此将不同G和τ取值下安全盆的尺寸(即安全盆内初值点的个数)与之相比，这样就可以计算出相应安全盆的面积大小(即面积百分比)。系统(2)的安全盆在取值范围－2≤x(0)≤2，－2≤y(0)≤2内的面积变化如图5所示。从时滞对安全盆面积的影响来看，时滞速度反馈对安全盆侵蚀起到了积极的控制作用。

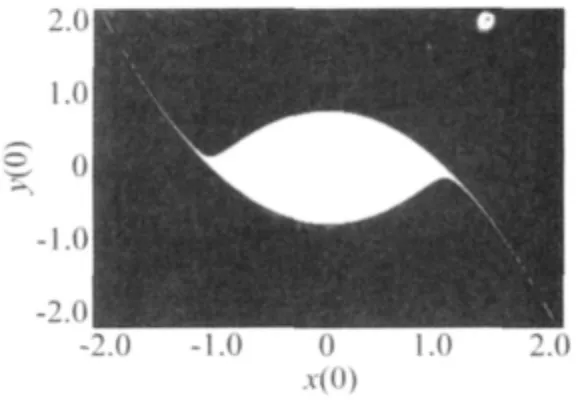
图4 c=0.01，G=0时系统(1)的安全盆Fig.4.The safe basin in system(1)when c=0.01 and G=0

图5 不同时滞下系统(2)的安全盆面积随激励振幅的变化图Fig.5.Variation of the basin area as the amplitude increases for system(2)under different values of time delay

由图5可知:不管有无时滞，安全盆面积都随激励振幅单调递减;外激励振幅较小时安全盆的侵蚀更易被控制成无侵蚀状态(见图5中水平虚线以上部分);安全盆面积随时滞的变化并不单调(由图中各折线存在交点可见)，但任何一种时滞取值非零的情况下，系统安全盆的面积都大于无时滞的情况。但时滞量较小时，激励振幅固定时，安全盆面积随时滞量单调递增(见图5中 τ=0，τ=2π/5和 τ=4π/5折线)。

3 结论

本文主要讨论了时滞速度反馈对一个软弹簧Duffing系统的安全盆侵蚀的控制。首先利用Melnikov函数法得到有时滞和零时滞情况下受控系统安全盆边界的分形条件。并本文将常微分方程系统的安全盆思想延拓到时滞微分方程所描述的时滞反馈系统，利用时滞系统无限维初始空间向有限维欧式空间投影的思想给出时滞反馈控制系统安全盆的定义。进而运用点映射蒙特－卡罗方法和龙格－库塔方法数值研究了时间滞后量对受控系统安全盆的影响规律，数值仿真结果与理论分析得到的安全盆边界的分形条件基本吻合。研究结果表明，时滞速度反馈可以有效地用于控制系统的安全盆侵蚀。但系统的安全盆的边界分形程度及尺寸并不是随时滞量单调变化的。当系统的反馈增益系数大于零时，一方面，当时滞量较小时，时滞的增大可以用来控制安全盆的分形侵蚀，降低系统崩溃的可能性;另一方面，一个大的时滞量也可能反过来引起安全盆的分形侵蚀。从动力学有关理论可以推断，时滞引起非线性系统安全盆侵蚀时系统的响应往往比较复杂，常常出现混沌响应，因此本文的结果在研究混沌控制方面存在潜在的应用价值。

［1］ Thompson J M T，Rainey F C T，Soliman M S.Ship stability criteria based on chaotic transients from incursive fractals［J］.Philosophical Transactions of the Royal Society，1995，332(1):149－167.

［2］ Marcos S H C，Lopes S R，Viana R L.Boundary crises，fractal basin boundaries and electric power collapses［J］.Chaos，Solutions and Fractals，2003，15(2):417 －424.

［3］Thompson J M T，McRobie F A.Indeterminate bifurcation and the global dynamics of driven oscillators［A］.In:Proceedings of 1st European Nonlinear Oscillation's Conference［C］.Hamburg，German，1983，107 －128.

［4］Soliman M S.Fractal erosion of basins of attraction in coupled nonlinear systems［J］.Journal of Sound and Vibration，1995，182(5):729－740.

［5］ Gan C B，Lu Q S，Huang K L.Non-stationary effects on safe basins of a softening Duffing oscillator［J］.Acta Mechanica Solida Sinica，1998，11(3):253－160.

［6］ Xu J，Lu Q S，Huang K L.Controlling erosion of safe basin in nonlinear parametrically excited systems［J］.ACTA Mechanica Sinica，1996，12(3):281－288.

［7］谷家扬，缪振华.随机海浪中船舶安全概率的数值模拟［J］.江苏科技大学学报(自然科学版)，2005，19(6):6－11.

［8］Hu H Y.Using delayed state feedback to stabilize periodic motions of an oscillator［J］.Journal of Sound and Vibration，2004，275(3－5):1009－1025.

［9］Wang H L，Hu H Y，Wang Z H.Global dynamics of a duffing oscillator with delayed displacement feedback［J］.InternationalJournalofBifurcation and Chaos， 2004，14(8):2753－2775.

［10］ Shang H L，Xu J.Delayed Feedbacks to Control the Fractal Erosion of Safe Basins in a parametrically excited system［J］.Chaos，Solitons ＆ Fractal，2009，41(4):1880 － 1896.

［11］尚慧琳，徐 鉴.时滞位移反馈Liénard振子的多稳态解［J］.同济大学学报 (自然科学版)，2008，36(7):962－966.

［12］陶 醉，张纬康.船舶横甩吸引域的数值研究［J］.海军工程大学学报，2002，14(2):59－63.

Control for erosion of safe basins in a softening duffing oscillator with velocity-delayed feedback

SHANG Hui-lin

(School of Mechanical Engineering，Shanghai Institute of Technology，Shanghai 20035，China)

In order to use delayed feedback controlling erosion of safe basins in nonlinear systems，a softening Duffing oscillator was considered here as an example，a linear delayed velocity feedback was induced to the system，and the effects of the delayed velocity feedback on controlling basin erosion were investigated.Firstly，the condition of fractal erosion of safe basin's boundary of the delayed controlled system was obtained by using Melnikov method.Then，considering time delay as a variable parameter and employing 4th-order Runge-Kutta and Monte-Carlo methods，the evolutions of boundaries and the area of safe basins with the delay were presented.It was found that the delayed velocity feedback can greatly affect the safe basin，and the erosion of the safe basin can be reduced with increase in the time delay effectively.It was shown that the delayed velocity feedback can be used as a good approach to control erosion of safe basins.

softening Duffing oscillator;erosion of safe basin;time delay;feedback;fractal

TP242;O322

A

国家自然科学基金青年基金项目(10902071);上海高校选拔培养优秀青年教师科研专项基金(YYY08004);上海市教育委员会重点学科建设项目(J51501);上海应用技术学院科学技术发展基金(KJ2011－06)

2011－01－02 修改稿收到日期:2011－04－25

作 者 尚慧琳 女，博士，副教授，1983年3月生