矢量波动方程的新瀑布型多重网格方法

陆康梅，李郴良，曹艳斌

(桂林电子科技大学数学与计算机科学学院，广西桂林541004)

在微波理论和技术中，谐振腔本征值问题是最基本的问题之一．很多微波部件和系统的分析与最优化设计又往往以该问题的求解为基础．矢量有限元方法是近10年来在电磁场计算中应用比较广泛的一种方法．只要选择了合适的矢量基，所考虑结构的内部和外部边界都能够从数学上自然满足，就能够很好地解决伪解问题;又因为有限元方法的网格划分能很好地模拟实际结构，因此我们选择了矢量有限元对谐振腔进行离散计算．

多重网格方法，对于求解由微分方程离散化得到的方程组来说，是目前最快速高效的方法之一，它的求解的工作量可降为O(n)或O(nlnn)．因此它在计算电磁场问题上得到了广泛的关注，最近一些学者发展了基于棱边元的多重网格算法［1－6］．瀑布型多重网格无需粗网格校正，它比一般的多重网格方法计算量减少了，从而提高了计算效率，然而基于棱边元上的瀑布型多重网格方法的研究还是比较少的，特别是矢量场的本征问题，目前研究的也较少．

外推算法是由林群，陈传淼等［7－8］引入到有限元求解偏微分方程，杨一都在文献［9］中引进了本征有限元外推的一个新技术，李永明等［10］将有限元外推应用到了波导本征问题．本文在其基础上，将其推广应用到矢量波动本征问题，具体的算例表明其可行性和高精度性．

本文结合外推技术，提出了一种基于矢量场本征问题的瀑布型多重网格方法．数值算例结果说明该方法的有效性和实用性．

1 数学基础

对于一个填充相对介电常数为εr和相对磁导率为μr介质的封闭谐振腔体，对应的矢量波动方程为

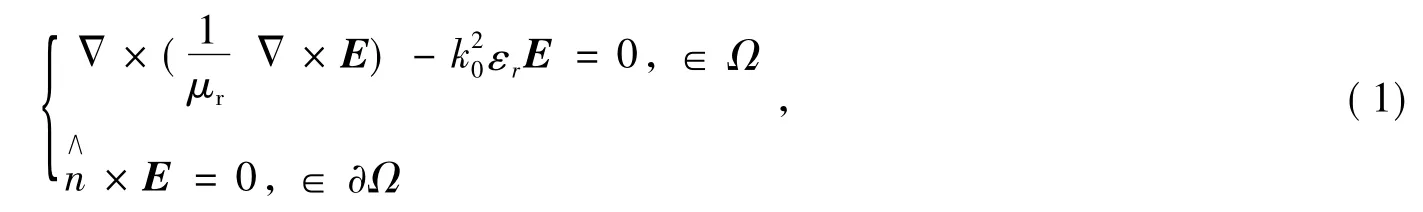
其合适的变分公式为

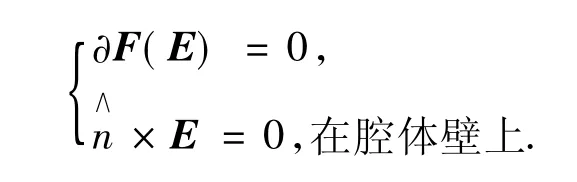
其中

这里S为谐振腔的面积．为了离散F，我们把S细分为小的矩形，每个小块占有面积Se(e=1，2，3，…，M)，其中M是单元总数．在每个单元中，电场近似为

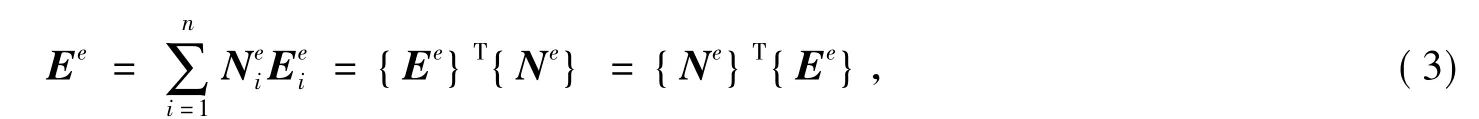
其中

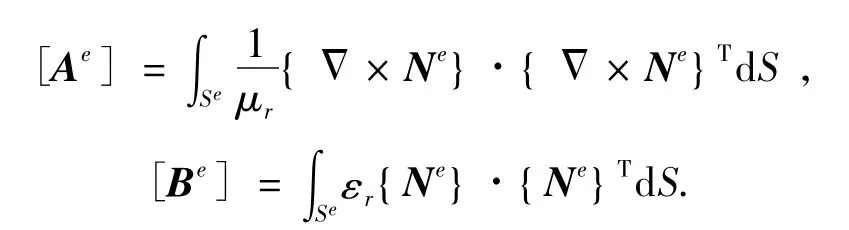
Se表示单元面积．在进行求和并使用全局编码后，(4)式可写

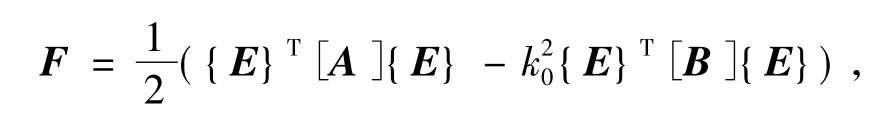
应用里兹方法，可得到本征方程组

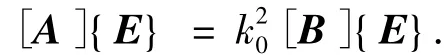
在强加狄利克雷边界条件以使得腔体壁上的棱边场为0后，由上式可解出本征值k20和对应的本征向量．

2 求解矢量场本征问题的瀑布型多重网格法

对于不同的剖分步长，矢量有限元离散方程(1)产生的相应的一系离散方程组

需要求解最细网格层上的本征方程，即Alul=λlBlul．本文将提出一种求解矢量场本征问题的瀑布型多重网格方法．该方法是一种基于棱边上的线性插值多重网格方法，并通过共轭梯度法来改善多重网格迭代的收敛性，并结合了外推技术提高解的精度．本文还将文献［10］中的基于节点元上的外推方法推广至棱边元上，具体的算例表明算法具有高精度性．

2．1 棱边上的插值算子

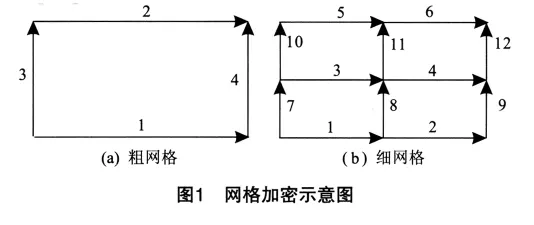
在求得粗网格层上的本征向量ul－1后，我们通过线性插值可以得到细网格层上的本征向量ul，

其中P为线性插值算子，矩阵P的构造可有下式得到［1］

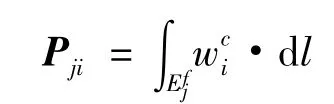
再根据Rayleigh商公式可以得到细网格上的近似本征值．

2．2 光滑过程

由上述的(5)式和(6)式，可以得到细网格上本征问题

的近似本征值˜λl和本征向量˜ul，我们可以以它们作为初始的迭代特征对，通过迭代过程可以得到细网格上的更好的近似解λl，ul．共轭梯度法是求解稀疏线性方程组，特别是对称正定方程组的最有效的方法之一，并且矩阵和向量相乘的次数也比较少，所以本文的迭代过程采用了文献［11］提出的求解本征问题的共轭梯度迭代．

令方程(7)的右端项为

则求解方程(7)的共轭梯度法的迭代过程如下：

算法 1［11］(NCGM)

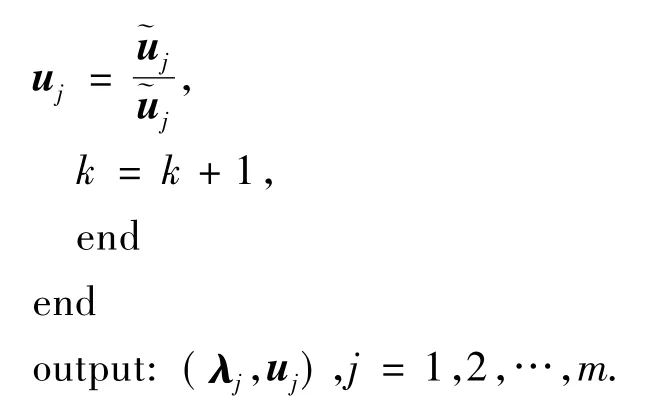
其中ε为精度控制参数．以上迭代过程简记为(λj，uj)=

2．3 外推技术

定理1 设剖分是强正规的，又设λ为对应于波导本征问题的简单本征值，相应的规格化本征函数u∈C4(Ω)，则本征值外推估计为：

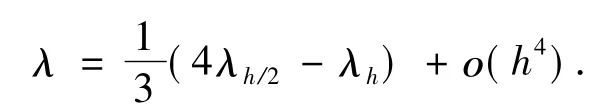
详细证明见文献［9］．

类似的，设某矩形谐振腔在粗矩形剖分单元下计算得到的本征值为λh，随后在此粗剖分基础上加密剖分1次，再计算得到的本征值为λh/2，则根据定理1，此矩形谐振腔本征值可由外推记为 λhw=E(λh/2，λh))，得到更精确的解．

2．4 矢量波动本征问题的瀑布型多重网格算法

对于矢量有限元离散产生的一系列本征方程组Aiui=λiBiui(i=0，1，2，…，l)，若要求解最细网格层l层上本征方程Alul=λlBlul，我们结合外推技术给出如下求解该本征问题的新瀑布型多重网格算法．

算法2GWCMG

表1 最细网格(128×128)层上本文的GWCMG方法的数值结果

3 数值算例及分析

矢量波动方程一般出现在电磁学中的腔体谐振问题以及波在封闭或开放结构中的传播问题．而在这些问题中，人们关注的是确定对应于本征值的谐振频率或转播常数和对应的谐振模式或转播模式，它们一般都可以由特征值来确定，因此关键是特征值的求解．下面我们以求解矩形谐振腔本征值(谐振频率)问题为例，其尺寸为(a×b)=2m×2m，计算矩形谐振腔的一些模式的本征值，并将以上算法得到的解λGWCMG、一般瀑布型多重网格方法解λCMG、一般有限元解λFEM和真解λ进行比较，并分别列出其与真解的相对误差，分别表示为eGW、eCM和eF．

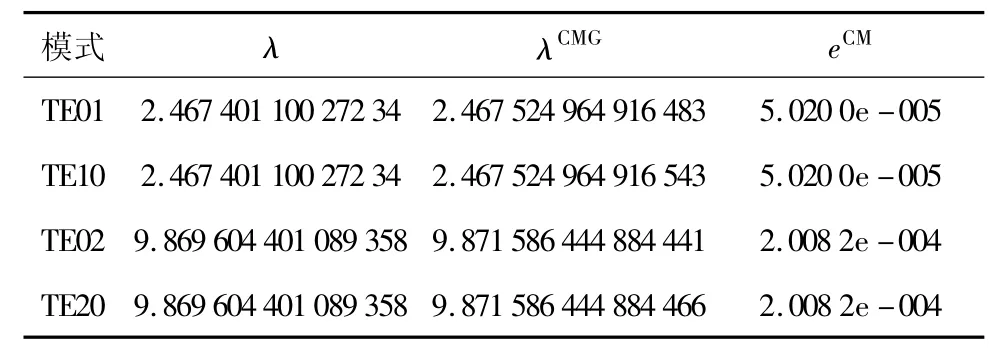
表2 最细网格(128×128)层上一般瀑布型多重网格法的数值结果

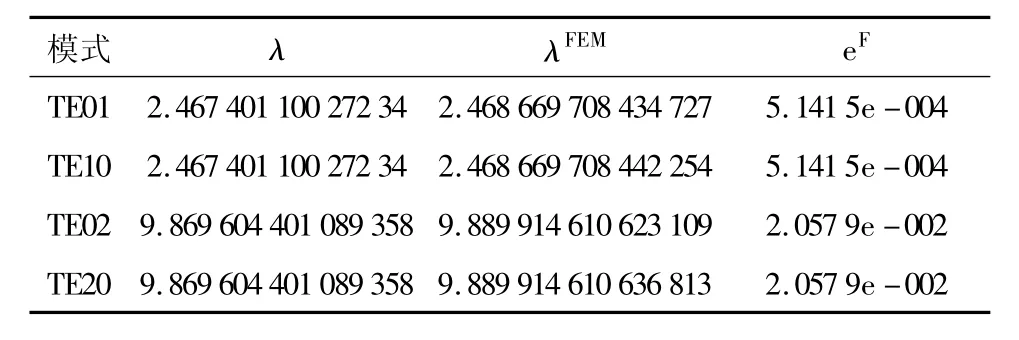
表3 最细网格(128×128)层上一般有限元法的数值结果

由表1，表2和表3可以看到本文的算法使计算精度得到了很大的提高．

由图2，我们也可以看出随着网格的加密计算的精度越来越高，从而验证了算法的快速收敛性，且和一般的瀑布型多重网格方法比较计算精度也提高了很多．

4 结语

从上述的算法公式，以及矩形谐振腔的谐振频率计算结果的分析可以看到，利用瀑布型多重网格方法大大减少了计算量，将外推推广应用到谐振腔本征问题求解精度得到了很大的提高，因此在比较少的单元剖分下便可以较大的提高计算精度．计算过程也比较简单，易于编程，因此该算法在现代数值计算中是一种十分实用、简单、高效的新方法．

［1］ WATANABE K ，IGARASHI H ．Robustness of nested multigrid method for edge－based finite element analysis［J］．IEEE Transactions on Magnetics，2009，45(3)：1 088 －1 091．

［2］ TSAI C L ，WANG W S ．An improved multigrid tcchnique for quasi－TEM analysis of a microstrip embedded in an inhomogeneous anisotropic medium［J］．IEEE Trans．Microwave Theory Tech，1997，45(5)：678 －686．

［3］ WEISS B ，BIRO O ．Edge element multigrid solution of nonlinear magnetostatic problems［J］．Comple，2001，20(2)：357 －365．

［4］ SCHINNERL M ，SHOBERL J ，KALTENBACHER M．Nested multigrid methods for the fast numerical computation of 3D magnetic fields［J］．IEEE Trans Magn，2000，36：1 539 －1 542．

［5］ WATANABE K ，IGARASHI H ，HINMA T．Comparison of geometric and algebraic multigrid methods in edge－based finite－element analysis［J］．IEEE Transactions on Magnetics，2005，41(5)：1 672 －1 675．

［6］金建铭，王建国，葛德彪．电磁场有限元方法［M］．西安：西安电子科技大学出版社，2001：165－186．

［7］陈传淼，黄云清．有限元高精度理论［M］．长沙：湖南科学技术出版社，1995：451 －492．

［8］李郴良，陈传淼，许学军．基于超收敛和外推方法的一类新的瀑布型多重网格方法［J］．计算数学，2007，37(9)：1 083 －1 098．

［9］杨一都．本征值有限元外推的一个新技术［J］．贵州大学学报：自然科学版，1989，6(3)：6 －11．

［10］李永明，俞集辉．有限元外推法在波导本征值问题中的应用［J］．重庆大学学报：自然科学版，1999，22(4)：78－81．

［11］匡前义，李郴良，李明．一种求解广义特征值的瀑布型多重网格方法［J］．云南民族大学学报：自然科学版，2009，18(3)：202 －205．