我国31个地区2001~2008年GDP时空分析
王立强,续秋霞,李海洋
(1.西藏民族学院信息工程学院,陕西咸阳712082;2.西安工程大学理学院,陕西西安710048)
从经济角度看,一个国家的GDP大幅增长,反映出该国经济发展蓬勃,国民收入增加,消费能力也随之增强.研究GDP有助于了解人民的收入,国家的收入,人民的就业情况以及维持社会的稳定等一系列问题.对于GDP时间上的研究与预测已有诸多文献[1-3],对于一个地区GDP空间上的文献近年来也不少[4-6].但同时对一个地区GDP时间空间上的研究并将其纳入一个模型仍鲜有.因此,针对此一系列问题,对我国不同地区GDP在各年中进行适当的研究及预测是很有必要的.本文对我国31个省区2001~2008年GDP数据与各地区的位置坐标数据,通过线性混合模型,分析了其时间空间结构特征,并且建立了相应的预测方程.
1 模型
线性混合模型为

Y是n×1观测向量,β是p×1称为固定效应.X和Z分别为n×p和n×q的已知设计矩阵.u和e分别为q×1和n×1随机向量,u为随机效应,e为误差.且E(u)=0,E(e)=0,u和e互不相关且cov(u)=G,cov(e)=R,G 和 R 为已知或未知正定阵,均值和Y的协方差矩阵是由E(Y)=Xβ和V=ZGZt+R分别给出的.线性混合模型的未知参数分2类,一类是固定效应,一类是方差分量.对模型(1)估计可估函数^β和^u,记

其中A=(XtV-1X)-1.但是G和R必须估计,然后和是由V∧θ和G∧θ分别替代V和G而得到的,其中,θ 是由方差组成的向量是 θ 的估计[7-8].

2 GDP的时间空间分析
本文数据集包含了2001~2008年31个省市共计248个GDP统计值,数据来源于陕西人民政府门户网站统计信息版块(http://data.sei.gov.cn/yearnew/a_search200809.asp),各省市的经纬度范围来源于软件Google Earth.
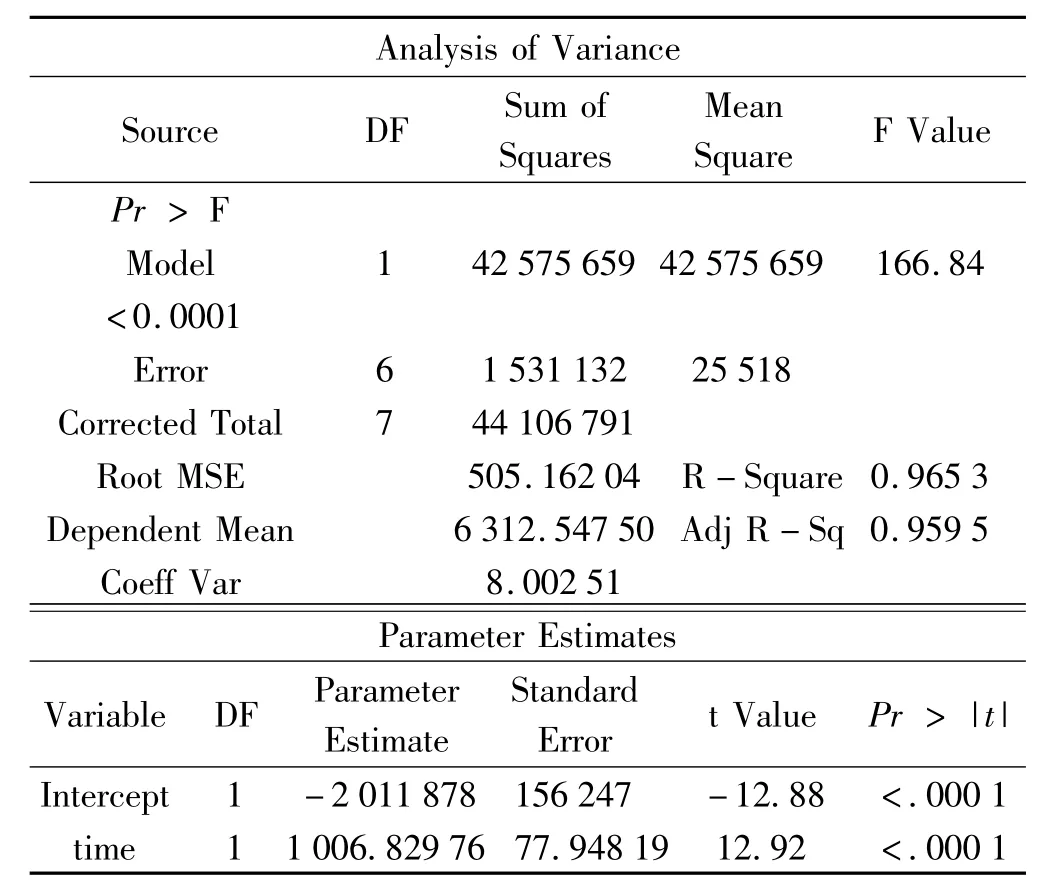
表1 GDP均值与时间的线性回归方差分析表与参数估计表
1)首先利用描述性统计量平均值对不同时间点的GDP变化趋势做一个简单描述.所做趋势图如图1所示.该图中,横轴表示时间,纵轴表示GDP值.从总的趋势来看,GDP曲线的斜率及增长速度逐年递增,但变化较小,大致可以看做一条直线,即time与GDP近似呈线性关系.
通过 SAS[9-10]统计软件拟合 GDP 均值与时间的线性回归结果见表1.
由表 1,回归模型的检验 P-值为小于0.000 1,调整后的R2为0.959 5,参数估计中时间的显著性检验P-值小于0.000 1,这些都充分表明,GDP均值与时间线性关系非常显著.
其次,分别做出GDP1~GDP8对应于2个坐标轴经度(east)和纬度(north)的描述曲线如图2~3所示.横轴表示坐标 east,north,纵轴表示2001~2008年的 GDP.由图2、图3显示 GDP1~GDP8与east和north之间为曲线关系.

方法同前面分别拟合east和north的多项式模型,得east为3次方,north为5次方.从而建立混合线性回归模型:


yi,j为第 i个地区 j年的 GDP 值(i=1,…,31;j=1,…,8),xi,1,xi,2,xi,3(i=1,…,31,)分别表示 east3,north5,time.

表2 方差协方差结构统计量(REML法)

表3 方差协方差结构统计量(ML法)
2)参数估计方法与协方差结构的选择.这是一个具有8个时间点的重复测量数据,在分析协变量的效应前,先要选择一个合适的方差协方差矩阵.分别用ML算法和REML算法进行分析,表2与表3分别列出了4种常用协方差结构在2种算法下的结果.在配合的4种协方差结构中,综合考虑协方差参数的个数及信息量指标值,特别是AIC准则,观察其大小变化,结果显示在ML算法下,以具有2个协方差参数的VC法效果最好.故本例选用ML法,用VC作为本例的方差协方差结构的算法.
3)模型结果.在VC方差协方差结构下,把随机项列入模型分析.反应变量Y为8个时间点的GDP值,随机项为地区.把east、north和time作为固定效应纳入回归方程中进行分析,得到协方差参数估计如表4.
协方差参数的检验P-值小于0.000 1,说明协方差VC结构是合理的.
模型中每一地区的8次重复测定之间的方差协方差矩阵 Rij(i=1,…,31,j=1,…,8)为:

表4 协方差参数估计

故R为一个由(31×31)个矩阵块Rij所构成的((8×31)×(8×31))的矩阵.
同样,可以得到随机效应的一个(31×31)的方差协方差矩阵G如下所示:

固定效应参数估计值及假设检验结果如表6所示.由检验P-值可以看出,我国31个地区8年的GDP值时间方向上变化更显著于地区性方向,即8年各个地区GDP的增长都是非常巨大的;同时,通过检验P-值也可以看出呈现出很强的南北差异与东西地域性差异,越往东GDP值增长越快,而越往北GDP增长越慢,而且在地理方向上东西方向引起的GDP增长差距要比南北更显著.这与我国的实际情况是相符合的,东南沿海地区明显要比内陆西北地区经济发达得多.
表7为随机效应参数的估计以及检验结果.在α=0.1的显著性水平下北京、天津、辽宁、山西、黑龙江、湖南、湖北、内蒙古、云南、西藏、陕西、甘肃、青海其随机效应不具有统计意义.

表5 固定效应的参数估计值及假设检验结果

表6 固定效应的Type3检验结果

表7 随机效应的参数估计值及假设检验结果

续表7
最后我国各地2001~2008年样本数据得到不同地点GDP的预测方程表达式为:

其中的值如表7所示,它表示不同地区的随机效应.由此可以预测这些地区中任意地区任意一年的GDP值.
[1]刘亮,孙朗成.我国GDP的非参数回归建模及其应用[J].沿海企业与科技,2009(10):20-22.
[2]郝香芝,李少颖.我国GDP时间序列的模型建立与预测[J].统计与决策,2007(23):4-6.
[3]于修柱.我国GDP增长与CPI变动的实证分析[J].内蒙古科技与经济,2005(12):24-25.
[4] 张晓旭,冯宗宪.中国人均 GDP 的空间相关与地区收敛:1978 ~2003[J].经济学:季刊,2008,7(2):399 -414.
[5]宋琳,董春,胡晶,等.基于空间统计分析与GIS的人均GDP空间分布模式研究[J].测绘科学,2006,31(4):123-125.
[6]赵军,杨东辉,潘竟虎.基于空间化技术和土地利用的兰州市GDP空间格局研究[J].西北师范大学学报:自然科学版,2010(5):92 -102.
[7]WOLFINGER R D.An example of using mixed models and PROC MIXED for longitudinal data[J].Journal of Biopharmaceutical Statistics,1997,7(4):481 -500.
[8] VERBEKE G,MOLENBERGHS G.Linear mixed models for longitudinal data[M].New York:Springer,2000:77 -119.
[9]余松林,向惠云.重复测量资料分析方法与SAS程序[M].北京:科学出版社,2004.
[10] Ramon C L.SAS for mixed models[M].Znded Cary,NC:SAS Institute,2006:317 -411.

