粘弹性人工边界的有限元分析

徐 浩

粘弹性人工边界的有限元分析

徐 浩

采用数值方法集中比较了工程中广泛应用的几种人工边界在 SSI体系分析中的动力反应,研究结果表明：粘性边界能较好的模拟土的边界但计算的位移会发生整体的飘逸,精度也不如粘弹性边界;粘弹性边界能很好的模拟土—结构相互作用体系中土的边界问题,但实现过程比较麻烦。

人工边界,SSI体系,粘弹性人工边界,有限元法

0 引言

土木工程中有许多涉及弹性半无限地基的振动及波动问题,诸如土—结构动力相互作用(SSI)问题、地震波的传播问题、动力机器基础的振动问题、打桩及道路交通引起的振动问题等。对这类问题用有限元法求解与用其他计算方法相比具有可灵活地适用于地基物性的不均匀性并可考虑地基的非线性特性等优点。但由于有限元法必须对求解对象的全领域进行离散,故在分析弹性半无限地基问题时必须截取一定范围的计算模型,这就要求在切取的边界上建立人工边界,用于模拟切除的无限域影响。目前人工边界主要分为两类：一类是全局人工边界条件,如边界元法等;另一类是局部人工边界条件,如旁轴近似人工边界、透射人工边界、粘弹性人工边界等。局部人工边界具有时空解耦的特点,得到了广泛的应用。其中粘弹性人工边界是通过沿人工边界设置一系列由弹簧和阻尼器组成的简单物理元件来吸收射向人工边界的波动能量和反射波的散射,其模型简单,物理意义清晰,便于在大型通用有限元计算软件中得到实现。ANSYS是一功能强大的有限元计算软件,其中的 ANSYS中的 Combin14单元和 LSDYNA中的Combin165单元,是弹簧与阻尼器的元件,易于实现粘弹性人工边界。本文在 ANSYS中实现了粘弹性边界并进行了验证和对比。

1 粘弹性人工边界

粘弹性人工边界作为一种应力边界条件,该应力是边界结点位移和速度的函数,一般形式写为：

由式(1)可以看出,粘弹性边界相当于在边界结点每个方向施加一个一段固定的单向弹簧—阻尼元件,而且该弹簧—阻尼元件的刚度和阻尼系数仅与该边界结点在该方向该时刻的反应相关,从而通过粘性阻尼的吸能作用和弹簧的刚性恢复作用模拟无限域对广义结构的影响。

1.1 二维粘弹性切向人工边界

当粘弹性人工边界为二维情况时,剪切边界条件利用平面内极坐标剪切波动方程,给出柱面剪切波的近似位移表达,从而建立平面应变剪切边界条件。

极坐标中出平面柱面波运动方程为：

其中,u为出平面位移;Cs为剪切波速,由公式 Cs=G/ρ确定,G为剪切模量,ρ为质量密度。

对于从坐标原点射出的柱面波可以采用如下形式的近似解：

可以看出,式(4)等价于一个阻尼系数为 ρCs的阻尼器并联上一个刚度系数为G/2ra的线性弹簧。这说明如果在半径 ra处截断介质,同时施加相应的边界元件后,在边界上可以得到与式(4)相同的形式,也即可以完全消除满足式(4)的出平面剪切波在边界处产生的反射波。

1.2 二维粘弹性法向人工边界

膨胀波边界利用平面内极坐标膨胀波波动方程,给出柱面膨胀波的近似位移势函数表达式,从而建立平面应变膨胀波边界条件。根据膨胀波的定义,设膨胀波位移函数为 u(r,t),并满足下式的纳维方程(忽略体力分量)：

其中,λ,G均为介质拉梅常数;Cp为介质膨胀波波速;ra为波源到人工边界点的距离;σr为人工边界节点ra在 t时刻的法向应力,σr=σr(ra,t);u为人工边界节点 ra在 t时刻的法向位移,u≈u(ra,t)。由于膨胀波是用位移势表达的,所以膨胀波边界是关于边界应力的一阶微分方程。图 1给出了膨胀波边界力学模型。

对比式(14)和式(9),可得各个物理元件的参数分别为：m=2ρra,C=ρCp,K=2G/ra。在实际运用中可以假定阻尼的质量端为固定,同时以上推导的二维粘弹性人工边界的弹簧和阻尼系数均需要乘以每个物理元件实际控制的单元长度。

1.3 三维粘弹性法向人工边界

三维情况是由球面波为基础推导的,其过程与二维情况大致一样,结论也非常类似。在三维情况下得到各个物理元件的相关参数为：m=2ρra,C=ρCp,K=4G/ra。在实际运用中可以假定阻尼的质量端为固定,同时以上推导的二维粘弹性人工边界的弹簧和阻尼系数均需要乘以每个物理元件实际控制的单元面积。

2 数值算例

力学模型如图 1所示,介质的剪切模量和密度取 G=1和ρ=1,泊松比取 0.25,剪切波和膨胀波的波速分别为和S(x)表达式如下：

为了使结果更具对比性,文章以同样的力学模型,将边界分别取为粘性边界和固端做了计算,以A点(0,2)为基准点,计算结果如图 2所示。

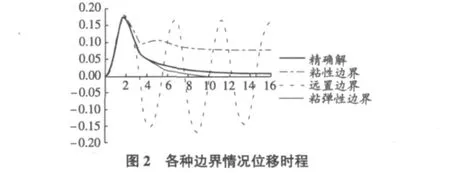
从图 2可以看出：粘弹性边界是所有边界中最接近精确解的,具有很好的精度;粘性边界大致趋势也符合精确解,但如前面所述,有明显的漂移现象;使用固定边界计算有明显的误差,故在以后的计算分析中应该极力避免使用固定边界。

3 结语

粘弹性人工边界在实际应用中能够结合通用有限元软件ANSYS等实现,通过编制命令流建模、求解,程序编制简单,修改方便,计算精度能够满足要求。但是针对较复杂的边界情况,编制粘弹性人工边界程序仍然有很大的难度,如何更好的去适应各种复杂的边界情况是以后的工作重点。

[1]廖振鹏,黄孔亮,杨柏坡,等.暂态波透射边界[J].中国科学,1984,26(6)：50-56.

[2]Lysmer J,Kulemeyer R L.Finite Dynam ic Model for Infinite Media[J].Journal of Engineering Mechanics.ASCE,1969(95)：859-877.

[3]Deeks A J,Randolph M F.Axisymmetric Time-domain Transmitting Boundaries[J].Journal of Engineering Mechanics,1994,120(1)：25-42.

[4]沈聚敏,周锡元,高小旺,等.抗震工程学[M].北京：中国建筑工业出版社,2000.

[5]刘云贺,张伯艳,陈厚群.拱坝地震输入模型中黏弹性边界与黏性边界的比较[J].水利学报,2006,37(6)：758-763.

[6]刘晶波,谷 音,杜义欣.一致粘弹性人工边界及粘弹性边界单元[J].岩土工程学报,2006,28(9)：1070-1075.

[7]刘晶波,王振宇,杜修力,等.波动问题中的三维时域粘弹性人工边界[J].工程力学,2005,22(6)：46-51.

[8]王振宇,刘晶波.成层地基非线性波动问题人工边界与波动输入研究[J].岩石力学与工程学报,2004,23(7)：1169-1173.

[9]刘晶波,杜义欣,闫秋实.粘弹性人工边界及地震动输入在通用有限元软件中的实现[J].防灾减灾工程学报,2007(27)：37-42.

[10]刘晶波,吕彦东.结构—地基动力相互作用问题分析的一种直接方法[J].土木工程学报,1998,31(3)：55-64.

[11]杜修力,赵 密.基于黏弹性边界的拱坝地震反应分析方法[J].水利学报,2006,37(9)：1063-1069.

The finite element analysis of viscoelastic artificial boundary

XU Hao

Concentrated compared the dynam ic response of several kinds of engineering extensive application artificialboundary usingnumerical method in SSI system analysis.Research results showed thatviscoelastic boundary can simu lation soil boundary well,overall d rift of calcu lation disp lacement will happen the precision is worse than viscoelastic boundary.Viscoelastic boundary can be a very good simulation for the problem of earth boundary in the soil structure interaction system,however,the realization p rocess is so troub lesome.

the artificialboundary,SSIsystem,viscoelastic artificial boundary,finite elementmethod

TU411.3

A

1009-6825(2011)09-0072-02

2010-12-04

徐 浩(1986-),男,同济大学土木工程学院建筑工程系硕士研究生,上海 200092