碳纤维布加固箱梁桥正截面强度的计算

韦成龙 , 何志军, 王光辉,

(1. 湖南理工学院, 湖南 岳阳 414006; 2. 长沙理工大学, 长沙 410076)

箱形梁桥抗扭刚度大、结构整体性能好, 是我国公路桥梁中十分常见的桥型. 然而, 目前许多在用箱梁桥不同程度的出现了裂缝, 这些裂缝的存在对结构产生了十分不利的影响. 碳纤维布(CFS)以其抗拉强度高、重量轻、极好的耐腐蚀性能及耐久性等优点, 已经在建筑、桥梁结构加固工程中得到了广泛应用, 然而CFS加固箱梁方面的研究少见报道. 本文采用有限元分析的方法, 对CFS加固箱梁的承载力进行研究.用等截面简支箱梁作为有限元计算模型, 考虑材料和几何双重非线性影响, 对结构进行非线性有限元计算. 通过对比计算研究, 确立计算模型的可靠性. 根据不同工况有限元仿真计算结果, 得出箱梁混凝土开裂、破坏全过程特性和规律, 在此基础上提出合理假设, 建立 CFS加固箱梁正截面强度计算的公式, 为CFS加固箱梁的正截面计算提供了简便的设计计算方法.

1 理论研究

采用非线性有限元理论, 借助ANSYS及其提供的参数化语言APDL编制相应的有限元计算程序, 建立CFS加固箱梁的三维非线性有限元分析模型, 进行受力全过程仿真分析, 计算结果与《公桥规》方法对比, 验证有限元计算方法的可靠性. 进而, 通过给箱梁施加不同的预应力, 进行箱梁正截面承载力的受力全过程有限元分析, 获得相应的CFS加固箱梁正截面的极限承载力. 在有限元分析的基础上, 整理总结出梁在正截面受力时的裂缝发展情况、荷载—挠度关系、纵向钢筋和碳纤维布的应变、极限荷载和破坏特征, 并提出加固设计的实用计算方法.

1.1 有限元计算模式以及单元类型的选择

在建立有限元模型时, 将普通钢筋弥散于混凝土中, 混凝土采用3维实体单元 Solid65模拟, 碳纤维布采用壳单元 Shell41模拟, 各种单元之间通过共用节点连接在一起, 形成分离式与整体式相结合的有限元模型. 进行非线性计算时, 在容易出现应力集中的部分, 设置弹性垫块, 避免混凝土过早的出现压碎或开裂破坏. 所以在有限元计算时, 支座的局部作用是通过施加在支座垫块节点上的约束来模拟, 集中荷载采用面荷载来模拟, 弹性垫块用 3维实体单元 Solid45来模拟, 并假定各种材料之间粘结完好, 钢筋与混凝土、CFS与混凝土之间没有相对滑移.

1.2 混凝土、预应力钢筋、碳纤维布的本构关系

在进行非线性计算时要用到材料的本构关系, 混凝土应力—应变关系采用二次抛物线加水平线的模式, 混凝土达到抗压强度前的上升段采用二次抛物线, 达到抗压强度后采用水平线.

其中极限压应变值uε=0.0033; 峰值压应变0ε=0.002;0σ为混凝土的峰值压应力, CEP-FIP规范采取0.85 σ0= 0.85fCK, fCK为混凝土标准圆柱体抗压强度.

对于高强度的钢绞线而言, 其应力—应变关系在条件屈服强度以前采用一种弹性模量, 超过条件屈服强度后, 采用另一种较小的弹性模量, 其应力—应变关系采用双折线模型:

其中σ和ε分别为钢绞线的应力和应变; fpy为钢绞线的条件屈服强度; E为钢绞线的弹性模量;E′为屈服点后的切线弹性模量, 约为0.1; Eyε为钢绞线的条件屈服应变, 预应力通过施加荷载来模拟.

碳纤维布为理想的线弹性材料, 碳纤维布应力—应变为线性关系.

其中σ为碳纤维布应力;fE为碳纤维布弹性模量; ε为碳纤维布应变;uε为碳纤维布极限拉应变.

1.3 混凝土开裂处理以及非线性求解

混凝土的抗拉强度很低, 容易开裂, 裂缝的出现会引起周围应力的突然变化和刚度降低, Solid65单元采用弥散裂缝模式(Smeared Cracking Model), 假定裂缝发生在单元内部, 用多条平行的裂缝穿过开裂混凝土单元来表示, 即将裂缝视为弥散在单元内部的微小裂缝, 开裂的混凝土仍然保持连续, 弥散裂缝模式不必增加节点和重新划分单元.

非线性计算中采用增量迭代混合法求解, 选用力与位移两种收敛准则, 力收敛准则使用二范数准则,精度设为0.05; 位移收敛准则使用无穷范数准则, 精度设为0.001.

2 有限元模拟计算

2.1 CFS加固箱梁正截面承载力的有限元离散模型

箱梁模型的基本尺寸如图1所示, 按照采用的单元类型, 根据箱梁各部位钢筋的不同, 分别进行分区分层单元离散, 其中高度方向为三层: 顶板部分(A), 腹板部分(B), 底板部分(C); 纵向分为Ⅰ、Ⅱ、Ⅲ区,见图 1, 有限元离散模型见图 2, 计算各区各层的钢筋的体积配筋率及方向角等参数, 考虑约束边界条件,模拟一期恒载、二期恒载、活载, 用荷载子步进行加载计算.

图1 二分之一箱梁有限元模型分区图(尺寸单位: mm)

图2 箱梁和碳纤维布的单元离散图

2.2 有限元计算结果

2.2.1 正截面承载力

从ANSYS软件强大的后处理功能整理出计算结果, 荷载作用下底板关键节点(标注为3137、3144两点)的荷载—挠度曲线见图3, 同时用《公桥规》提供的方法进行了计算, 对比结果见表1.

表1 《公桥规》方法和有限元模拟计算的结果对比

从表1可以看出, 有限元方法与《公桥规》方法的结果相差在5%内, 说明有限元模拟方法是可靠的.

图3 箱梁跨中截面关键点处的荷载—挠度曲线

2.2.2 正截面全过程模拟计算

在实际工程中, 箱梁大多用在预应力混凝土结构中, 因此在有限元模拟计算时,考虑了不同的预应力度. 利用上述计算方法, 对四片箱梁施加不同的预应力, 计算整理出不同预应力时的结果, 见表2.

由表 2可以看出: 预应力为纤维布强度的10%、20%、30%时, 开裂弯矩相比未施加预应力时分别提高2.7%、5.5%、8.6%,极限弯矩分别提高 4.9%、7.7%、10.5%,故随着预应力度的提高, 箱梁的开裂荷载和极限荷载不同, 碳纤维布的作用也不同.荷载—挠度曲线如图4所示.

表2 开裂弯矩和极限弯矩

由图 4可以看出: 对箱梁施加不同的预应力度, 极限承载力差别不大(与没有粘贴碳纤维布比较), 说明破坏时碳纤维布并没有达到设计强度.

2.2.3 全过程受力特点

碳纤维加固箱梁的受力特点可分为三个阶段, 如图5所示.

图4 四种工况跨中截面关键点荷载—挠度曲线

图5 碳纤维加固箱梁受力阶段分析

第一阶段(OA段): 底板混凝土开裂之前(弹性工作阶段). 有预应力箱梁弹性工作阶段较长, 开裂荷载得到提高.

第二阶段(AB段): 底板混凝土开裂至预应力钢筋屈服(带裂缝工作阶段). 由于碳纤维布与预应力钢筋共同承受拉应力,碳纤维分担一部分荷载, 使得预应力钢筋屈服时荷载得到提高.

第三阶段(BC段): 预应力钢筋屈服后至顶板混凝土压碎(碳纤维布增强阶段). 预应力钢筋屈服后, 裂缝向受压区延伸, 使压区面积减小, 压应力增大, 最终混凝土压碎破坏, 此时碳纤维布没有拉断.

2.2.4 破坏模式

由有限元计算结果可知, 构件破坏时碳纤维布的最终应力均小于极限抗拉强度, 说明在锚固措施可靠的情况下, 构件的破坏都是以钢筋屈服、混凝土压碎宣告破坏, 纤维布除非剥离破坏, 一般不会发生拉断. 且箱梁用碳纤维加固, 既能提高构件的承载力, 对箱梁的刚度也有改善.

3 CFS加固箱梁正截面强度的实用计算公式

3.1 计算的基本假定

根据理论计算结果, CFS加固箱梁的正截面破坏都是以受拉钢筋屈服、混凝土压碎、纤维布没有拉断宣告破坏, 其正截面抗弯承载能力计算采用下述基本假定:

(1)平截面假定. 对于箱梁, 从开始加载直到破坏的各阶段, 截面的平均应变基本上符合平截面假定.

(2)不考虑混凝土的抗拉强度. 在裂缝截面处, 受拉区混凝土大部分退出工作, 但在靠近中性轴附近,仍有一部分混凝土承担着拉应力, 由于其拉应力较小, 且内力偶臂也不大, 因此, 所承担的内力矩是不大的, 故在计算中可忽略不计.

(3)顶板部分混凝土的应力取用混凝土的抗压强度, 腹板部分混凝土的应力线性变化.

3.2 正截面抗弯强度计算公式

根据前面介绍的破坏形态和计算假定, 建立强度计算公式, 针对中性轴的位置的不同, 分为第I类(中性轴在翼缘内)和第II类截面(中性轴在腹板内), 其计算图式如图6所示.

图6 箱梁正截面受力图

(1)第I类箱梁截面

(2)第II类箱梁截面

(3)当x= h′1时, 有

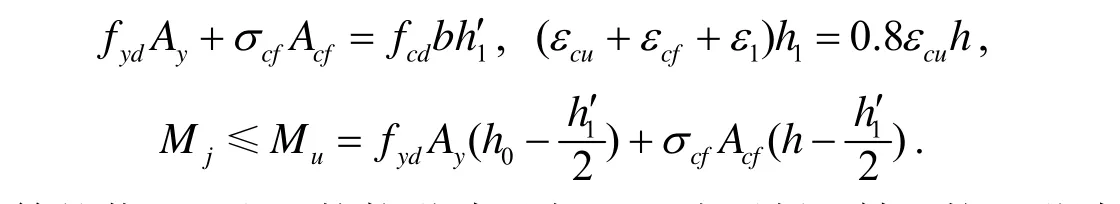
其中yA、ydf为受拉区钢筋的截面面积和抗拉设计强度;cdf为混凝土轴心抗压设计强度;x为对于第I类箱梁, 按等效矩形应力图计算的受压区高度; 对于第 II类箱梁, 为等效梯形受压区高度减去顶板厚度;b为箱梁的宽度;t为箱梁的腹板厚度;h1′为箱梁顶板计算厚度;h0为截面有效高度;Mj为作用在计算截面的弯矩效应;cuε、cfε为分别表示混凝土破坏时的极限应变、碳纤维应变;1ε为考虑二次受力影响时, 加固前构件在初始弯矩下, 受拉边缘混凝土的初始应变; 当不考虑二次受力时, 取0.

3.3 箱梁正截面加固计算方法

3.3.1 加固设计

若桥梁荷载等级提高(如道路等级提高、超载), 一般需要进行正截面加固设计, 计算CFS的数量Acf. 通过试算法确定类型后, 利用上述基本方程联立求解, 即可得到CFS的数量.

3.3.2 加固强度复核

对加固的箱梁进行强度复核, 已知 CFS的数量, 截面尺寸, 钢筋数量和混凝土强度, 通过试算法确定类型后, 根据基本公式进行复核.

4 结论

通过有限元仿真计算, 对CFS加固箱梁正截面的受力破坏过程进行了全面的研究. 在有限元分析计算与现有加固设计规范的基础上, 提出了CFS加固箱梁正截面的计算方法和相应的计算公式, 为CFS加固箱梁的设计提供参考.

[1]陈道勇. 碳纤维布加固斜交空心板的强度研究[D]. 长沙: 长沙理工大学博士学位论文, 2008, 5

[2]程莉莎, 程晓东, 叶贵如. CFRP加固钢筋混凝土梁极限承载力的三维非线性分析及试验研究[J]. 工程力学, 2005, 22(6): 175～180

[3]王荣国, 代成琴, 刘文博, 等. CFRP加固混凝土梁抗弯极限承载力的计算分析[J].哈尔滨工业大学学报, 2002, 34(3): 312～314

[4]李忠献, 景 萌, 苏 标, 等. 碳纤维布加固弯剪扭复合受力的钢筋混凝土箱梁抗扭性能的模型试验研究[J]. 土木工程学报, 2005, 38(12): 38～45

[5]李忠献, 张 媛, 景 萌. 碳纤维布加固复合受力的钢筋混凝土箱梁抗扭性能的非线性有限元分析[J]. 工程力学, 2006, 23(增刊1): 122～128

[6]中国工程建设标准化协会. CECS146: 2003. 碳纤维片材加固修复混凝土结构技术规程[S]. 北京: 中国建筑出版社

[7]JTJ/T J22-2008. 公路桥梁加固设计规范[S].

[8]交通部. JTG D62-2004. 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].