方位角(α,β,γ)能确定刚性分子的自由度吗？

魏静

(电子科技大学微电子与固体学院 四川 成都 611731)

滕保华

(电子科技大学物理电子学院 四川 成都 610054)

杨婷婷

(电子科技大学微电子与固体学院 四川 成都 611731)

大学物理教材中在分析理想气体刚性双原子分子的自由度时，通常采用三个方位角(α，β，γ)并借助公式cos2α+cos2β+cos2γ=1，来确定其中两个独立方位角，由此得出刚性双原子分子转动自由度为2的结论．例如，文献[1]写道：“刚性双原子分子……连接两个原子的刚性键的方位仍可改变，分子的位置仍未确定，因此还另需要两个方位角来决定其键联的方向(三个方位角α,β,γ中，因有cos2α+cos2β+cos2γ=1的关系约束，故只有两个是独立的)，这两个角坐标实际上给出了分子的转动状态，因此双原子分子有三个平动自由度和两个转动自由度……”文献[2]写道：“……确定轴线方位需用α,β,γ三个方位角,但因这些方位角的余弦的平方和恒等于1,所以其中只有两个是独立的……”文献[3]写道：“……还需要确定它的两原子的连线的方位，这又需要两个独立坐标(一条直线在空间的方位，可用它与x,y,z轴的三个夹角α，β，γ确定．但因总有cos2α+cos2β+cos2γ=1，所以只有两个夹角是独立的)”．文献[4]写道：“……为了确定刚体绕过质心O′的轴的转动状态，首先要确定该轴在空间的方位，这可用三个方向余弦(cosα，cosβ，cosγ)表示，但由于三者存在着cos2α+cos2β+cos2γ=1的关系，所以三个量中只有两个是独立的，即确定转轴方位的自由度仅有2个．”

我们认为用方位角(α，β，γ)解释转动自由度的个数是不准确的．三个方位角虽然由公式cos2α+cos2β+cos2γ=1约束，但是该方程是关于α、β、γ的非线性方程，因此由其中任意两个方位角不能唯一确定第三个方位角．例如已知β和γ，可以确定cos2α，但不能唯一确定α．两个固定的方位角β和γ，分别对应两个不同的锥面.为了形象地说明这个问题，我们分两种情况进行讨论．

(1)若两个锥面恰好相切，则两个固定的方位角β和γ可以唯一确定直线的方向, 即切线方向，如图1所示.

图1 当两个锥面相切时，切线具有确定的取向，

(2)若两个锥面相交，则两个固定的方位角β和γ将使α有两个取值，即交线有两种可能的方向，如图2所示．

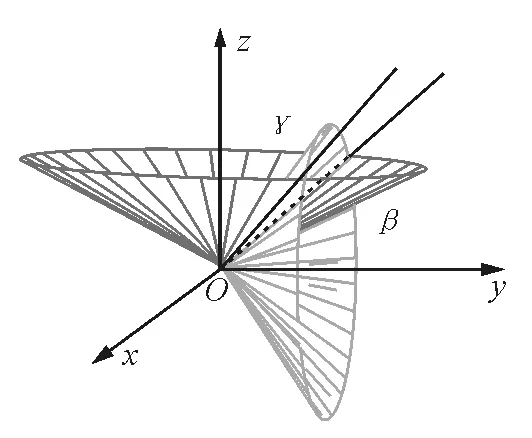
图2 当两个锥面相交时，交线的取向有两种情况，

综上所述，确定的β和γ不能唯一确定直线的空间方位．也就是说，三个方位角不能因为公式cos2α+cos2β+cos2γ=1的约束，而确定其中两个独立的方位角；即不能由此得到刚性双原子分子具有两个转动自由度的结论．

实际上，刚性双原子分子的转动自由度确实只有两个，如用球坐标系(r,θ,φ)就可以方便地说明.在球坐标系中，r是到原点的距离，与方向角无关，而θ,φ能唯一确定连线的方向．因此，对于空间方位来说，球坐标系中θ,φ是独立的，由此可知刚性双原子分子的转动自由度为两个．

由此得到结论，大学物理教材中关于理想气体刚性双原子分子的转动自由度的个数，不能用通常的方位角(α，β，γ)来唯一确定，但用球坐标系则可．

1 罗益民，余燕主编.大学物理(第二版).北京：北京邮电大学出版社， 2004.142～143

2 吴百诗主编.大学物理(下册).西安：西安交通大学出版社， 2004.47～48

3 张三慧主编.大学物理学(第二册)热学.北京：清华大学出版社， 2000.44～45

4 严导淦主编.物理学教程(上册).上海：同济大学出版社， 2007.256