基于ANSYS平台的桥梁时域颤振分析

卿前志

(上海市政工程设计研究总院(集团)有限公司， 上海 200092)

随着桥梁结构跨径的日益增加，结构的颤振稳定性能成为设计过程中重要的控制因素之一。对结构颤振稳定性能研究的主要目的是确定结构的颤振临界状态，揭示颤振发生的机理，从而保证结构的抗风稳定性。目前评价桥梁的颤振性能主要有三种方法，即经典理论法、风洞试验测试法和试验加理论法[1, 2]。

至今为止，结构颤振分析求解方法包含频域和时域两大类方法。频域范围内对颤振问题进行求解的基本思路为：首先将气动力用Scanlan自激力表达式[3]进行表达，然后通过求解结构运动特征方程得到结构颤振临界风速和颤振频率。频域分析属于线性分析方法，与之相比，时域分析能方便地考虑各类非线性因素的影响，并反映结构在颤振后的振幅演变规律，有利于基于过程性能的桥梁气动性能研究，因而近年来发展迅速。在时域范围对桥梁颤振稳定性进行求解首先需要得到时域化的气动自激力表达式，再在动力有限元中进行求解[2]。对于明显存在流动分离的钝体桥梁断面而言，以颤振导数表示的自激力是一种时频混合表达式，通常不能直接用于时域颤振分析，需要转换成等效的时域表达。目前，颤振时域分析气动力的表达方法有两种。其一是通过脉冲响应函数结合有理函数进行表达[4, 5]；其二是采用阶跃函数结合桥梁断面的气动导数进行自激力模拟[6]。本文采用第一种形式，首先得到桥梁断面的脉冲响应函数所表达的气动自激力，再对其进行动力有限元求解。

由于ANSYS软件具有良好的二次开发功能，可以应用于桥梁频域颤振分析中[7]，但相关文献对ANSYS应用于桥梁时域颤振分析的报道较少。文献[8]中虽然提出了一种在ANSYS中实现颤振时程分析的方法，但是，其必须同时对频率和风速进行搜索，因此实质上仍然是一种频域方法。本文提供了在ANSYS中实现颤振时程分析的另一方法，在瞬态动力学分析过程中嵌入气动自激力的递推算法来考虑其运动状态历史记忆特性，得到结构的颤振临界风速。本文的方法也适合其他风振问题，如颤抖振时域分析中的气动自激力模拟。

1 气动自激力脉冲响应函数表达

结构体系的运动方程为：

(1)

式中[M]、[C]、[K]分别为结构质量矩阵、阻尼矩阵和刚度矩阵，{Fa}为结构上受到的荷载列向量，当用于颤振分析时，其可以用气动自激力的形式表达。忽略断面侧向振动的影响，断面单位长度气动自激力可采用如下形式：

Lse=

(2)

Mse=

(3)

当采用脉冲响应函数对断面自激力进行表达时，同样，忽略断面侧向振动的影响，将竖向运动和扭转运动对断面自激力的贡献分开，则断面单位长度气动自激力可表示为：

Lae=Lsea(t)+Lseh(t)

(4)

Mae=Msea(t)+Mseh(t)

(5)

式中Ifx(f=M，L；x=α，h)为相应的脉冲响应函数，其直观意义为单位脉冲位移引起的气动自激力。

根据脉冲响应函数表达的气动自激力与Scanlan气动自激力表达式两者频谱特性一致，可得脉冲响应函数与颤振导数之间的关系式：

(6)

(7)

(8)

(9)

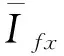
(10)

式中，ALh1、ALh2、ALh3、ALhi、dLhi(dLhi≥0；i=4,…,m)都是待拟合的参数。第一项和第二项分别表示由位移项引起的气动力和速度项引起的气动力，第三项表示由加速度项引起的气动力，该项通常较小而被忽略，第四项用于描述滞后于速度项的气动力非定常部分，m的大小决定了这种近似的精度和附加方程的数量，所有这些参数可以通过试验提取的颤振导数进行非线性拟合而确定[9]。

当得到有理函数的相关系数后，对式(10)做傅里叶变换，可得到脉冲响应函数的表达式：

(11)

代入式(4)中，有：

Lseh(t)=

(12)

对上式中的积分项进行一次分步积分，可以得到Lseh(t)的最终表达式如下：

(13)

有了式(13)的表达式后，在进行计算时，必须将卷积积分表达式转化为递推关系表达式。从式(13)易知，只需要解决Lseh2(t)的计算问题，该式可通过以下方法完成递推：

令

(14)

则

Zi(t+Δt)

(15)

同理可以得出Lseα(s)、Mseα(s)、Mseh(s)相应的表达式。

得到断面的气动自激力表达式后，即可方便地在ANSYS中实现颤振时程分析。在ANSYS中节点速度和加速度的获得，参照ANSYS帮助文件，对于采用Newmark法的时程分析，节点加速度和速度可表示为如下差分格式：

(16)

(17)

式中α=1/4(1+γ)2，δ=1/2+γ，γ为振幅衰减系数，即数值阻尼因子，ANSYS中默认为0.005，{un}及{un+1}为结构前一时刻运动状态量和结构当前时刻运动状态量，Δt为计算时间步长，根据式(16)、(17)即可通过前一时刻的速度、加速度及当前时刻的位移求得当前时刻的速度和加速度大小，逐步提高风速，便可得到结构的颤振临界风速。图1给出了在ANSYS有限元分析软件中实现颤振时程分析的计算流程。

图1 ANSYS颤振时程分析流程

2 数值算例

为验证本文计算模型和求解方法的正确性，采用文献[7]中具有理想平板断面的简支板梁进行ANSYS颤振时程分析验证。模型参数：长度L=300 m，宽40 m，约束两端扭转自由度。平板断面竖向和横向刚度分别为EIz=2.1×106MPa·m4，EIy=1.8×107MPa·m4，扭转刚度GIx= 4.1×105MPa·m4。每延米长度质量m=20000 kg/m，质量惯矩Im=4.5×106kg·m2/m，空气的密度ρ=1.248 kg/m3。建模时质量矩阵采用集中质量矩阵形式。桥面主梁采用BEAM4单元，质量惯矩采用MASS21单元模拟，整个模型具有30个桥面梁单元和29个扭转质量单元。为便于和文献[7]对比，结构阻尼设为零。

对理论平板气动导数进行有理函数参数拟合，表1列出了拟合结果。图2为拟合曲线和理论曲线的对照。从图2可以看出，由拟合有理函数参数反算颤振导数和理论颤振导数之间差别较小，拟合结果具有较高的精度。

表1 理想平板有理函数拟合参数

图2 理想平板颤振导数拟合值与理论值的比较

图3 跨中位移时程(U=135.5 m/s)

对有理函数参数拟合后，给结构施加初始激励进行动力响应分析，逐步提高风速，便可得到结构的颤振临界风速。图3、图4、图5分别为风速135.5 m/s、136.6 m/s及138 m/s简支梁跨中点位移响应曲线。由图3可知风速为135.5 m/s时跨中点竖向及扭转位移是衰减的。由图4可知风速为136.6 m/s时跨中点竖向及扭转位移具有等幅特性。从图5可知当风速为138 m/s时，结构振动位移出现明显的发散现象。得到结构的颤振临界风速136.6 m/s，对颤振临界状态位移响应时程做频谱分析得到结构的颤振频率为f=0.3906 Hz，与文献[7]中提供的颤振临界风速精确解U=136.3 m/s及颤振频率f=0.3914 Hz非常接近。

图4 跨中位移时程(U=136.6 m/s)

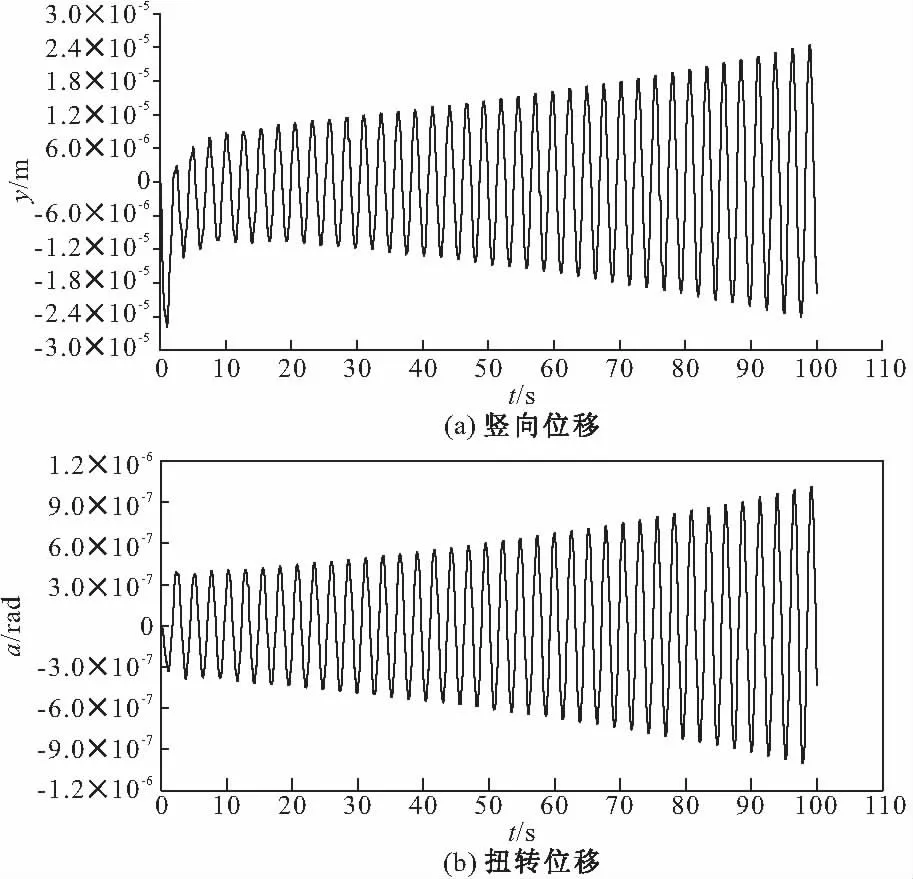
图5 跨中位移时程(U=138 m/s)

3 结 论

桥梁时域颤振分析在非线性特性模拟、后颤振形态以及结构风振全过程再现等方面具有频域方法不可代替的优势，因此时域颤振分析在将来的大跨桥梁抗风研究中将会得到越来越广泛的应用。本文的算例表明，基于拟合的气动自激力，在ANSYS中能方便地实现颤振自激力的施加，计算得到的颤振临界风速和相关文献中的报道结果吻合良好。本文的研究表明，利用ANSYS平台的二次开发功能进行桥梁气动稳定性能的时域分析是可行的，这一方法可为桥梁颤振分析或颤抖振理论分析提高效率，降低自主开发大型软件过程中的算法错误或疏漏所带来的风险。最后，需要指出的是，采用本文时域方法对颤振临界风速求解的关键在于脉冲响应函数参数的拟合，文中采用最小二乘法。若断面颤振导数随折算风速变化非常剧烈，尽管能得到折算风速范围内全局最优参数，仍可能引起自激力的模拟失真，可尝试其他参数拟合方法，继而利用ANSYS数值计算平台进行时域颤振分析。

[1] 陈政清. 桥梁风工程[M]. 北京：人民交通出版社，2005.

[2] 项海帆. 现代桥梁抗风理论与实践[M]. 北京：人民交通出版社, 2005.

[3] Scanlan R H, Tomko J J. Airfoil and bridge deck flutter derivatives[J]. Journal of Engineering Mechanics, ASCE, 1971,97(6): 1717-1737.

[4] Li Q C, Lin Y K. New stochastic theory for bridge stability in turbulent flow[J]. Journal of Engineering Mechanics, ASCE, 1995, 121(1): 102-116.

[5] Lin Y K, Yang J N. Multimode bridge response to wind excitations [J]. Journal of Engineering Mechanics, ASCE,1983, 109(2): 586-603.

[6] Scanlan R H. Motion-related body force functions in two-dimensional low-speed flow[J]. Journal of Fluids and Structures, 2000, 14: 49-63.

[7] Hua X G, Chen Z Q, Ni Y Q, et al. Flutter analysis of long-span bridges using ANSYS[J]. Wind and Structures, 2007, 10(1): 61-82.

[8] 华旭刚，陈政清，祝志文．一种在ANSYS中实现颤振时程分析的方法[J]．中国公路学报，2002, 15(4): 32-34．

[9] 张志田. 大跨度桥梁非线性抖振及其对抗风稳定性影响的研究[D]. 上海：同济大学，2004.