基于RS和PCA的大型工程目标集成化动态分析

陈黎明， 赵 辉

(青岛理工大学 管理学院， 山东 青岛 266520)

对大型工程目标进行科学化管理是项目成功的关键，而质量、费用和工期管理是大型工程的三大目标，三者相互依存、相互影响。在以往的研究中，以单目标因素分析较为常见，如陈东方、陈建国根据预警理论和方法，结合工程进度管理的特征，建立了工程进度预警模型[1]，张浩、吴炜煜提出了基于合约事务的工程项目费用管理结构体系，实现了一个以合约事务为基础的新型项目费用管理系统[2]。此外，还有针对三个目标中的两个进行研究，如熊鹰、匡亚萍采用蚁群算法针对施工项目中的工期成本优化问题进行研究[3]，吴二军、黄俊等人通过结合建筑物整体平移工程中的管理经验，探讨了新技术建筑工程施工中的质量和工期管理[4]，张增群、王毅等人提出了建筑工程设计质量寿命评价和全寿命周期费用评价并建立了相应的评价模型[5]，而目前对工期、成本和质量三者进行集成化的研究并不多见。鉴于此，提出了一种基于RS(粗糙集)和PCA(主成分分析)的大型工程质量、费用和工期集成化动态分析方法。

1 基础理论

1.1 粗糙集

粗糙集(RS-Rough Set)理论是20世纪80年代初由波兰数学家Z Pawlak首先提出的一种分析数据的数学理论[6，7]。它是一种新的处理模糊和不确定性知识的数学工具。其主要思想是在保持分类能力不变的前提下，通过知识约简导出问题的决策和分类规则，知识约简是粗糙集理论的核心内容之一。在粗糙集理论中，知识的表示通过信息系统来完成，设S=(U,A,V,f)，其中S为知识表达系统，U为对象的非空有限集合或称为论域，A为属性的非空有限集合，V为属性的值域；f:U×A→V为一个信息函数。当信息系统中属性A=C∪D，其中C为条件属性，D为决策属性时，一个信息系统可以方便地用数据表格来表示，因此，信息系统也称决策表，利用决策表可以实现知识的简化。

设R是U上的一个等价关系，[x]R表示包括元素x的R等价类。若P⊂R，则∩P也是一个等价关系，称为P上的不可区分关系，记为[x]IND(p)。

设a∈A，若IND(A)≠IND(A-{a})，则a是A的一个不可约简属性；反之，称a是A的一个可约简属性。若∀a∈A都是不可约简的，则称集合A是独立的，否则称集合A是相关的。

设Q⊆P，如果Q是独立的，且IND(Q)=IND(P)，则称Q是P的一个简化。P中所有不可省属性的集合称为P的核，详细的Rough集的知识约简算法请参考文献[8]。

1.2 主成分分析

主成分分析(Principal Component Analysis)是将多个实测变量转换为少数几个不相关的综合指标的多元的统计分析方法，是研究如何将多指标问题转化为较少的综合指标问题。通过借助一个正交变换，将分量相关的原随机变量转换成分量不相关的新变量；从代数角度，即将原变量的协方差矩阵换成对角阵；从几何角度，即将原变量系统换成新的正交系统，使之指向样本点散布最开的正交方向，进而对多维变量系统进行降维处理。按照特征值提取的观点，主成分分析相当于一种基于最小均方误差的提取方法。其主要评价思想是利用降维的思想，在不减少原数据信息量的基础上把多个具有复杂关系的指标通过正交转换得出几个综合指标，使得在研究各种复杂问题时容易抓住主要矛盾，并且得出综合指标的权重线性组合评价模型。

2 基于RS和PCA的大型工程目标集成化评价模型构建

大型工程的质量、工期和费用是三大主要控制目标，其影响因素较多，因此在对大型工程项目目标集成化管理上比较困难。而RS理论可以有效地对指标进行约简，从而筛选出冗余指标，PCA是处理多指标问题进行降维的有效工具，因此结合使用，可以使综合评价模型更加合理。

2.1 基于RS理论的指标筛选

以青岛市某大型工程建设项目为例，对大型工程项目的质量、费用和工期进行指标构建，确定测评指标，可记为：X={x1,x2,…,xp}。根据文献[9]并结合相关资料，可建立大型工程项目质量、费用和工期指标体系，包括22个影响因素，见表1。

根据各指标对大型工程项目目标影响的重要程度，可将其分为四个等级：重要，较重要，一般，低，并以满分10分进行取值评分，见表2。

通过本文基金项目资助的调研，对参与本项目的10位专家和15位同行人员进行样本数据采集，最终筛选出20份有效样本，整理得到评价矩阵{xij}n×p，p为最初评价指标个数，n为样本数(被评价对象数)。如果样本中数据有逆向指标要进行正像化处理，通常取倒数即可。由于本文都是离散数据，不需要此步骤。可设这20组样本形成的集合为U={1,2,…,20}，属性集合A={x1,x2,…,x22}，对每个属性制定一个阀值，1表示达到标准(大于等于阀值)，0表示没有达到。例如对于x1，阀值设定为6.8，大于6.8的为1，否则为0(阀值的确定方法为：取与该大型工程类似的10个项目通过专家对评价指标的打分取算术平均值，其方法可参考文献[10])。由以上规则，原始数据可简化为表3。

表1 大型工程项目质量、工期及费用指标体系

表2 大型工程项目分项指标评分值

根据表3，由于x2、x5、x20对应的各属性值是相同的，这时只保留一个属性，假设为x2，删除x5、x20两列；属性x10、x11、x17对应的各属性值相同，假设只保留x10，删除x11、x17两列；属性x15、x21对应的各属性值相同，假设只保留x15，删除x21列；属性x9、x16对应的各属性值相同，假设只保留x9，删除x16列，因此得到表4。

下面寻找表4中可省的属性，其中U={u1,u2,…,u20}，属性集合为:

A={x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19,x20,x21,x22}；

U/IND(A)={{1},{2},{3},{4},{5},{6},{7},{8},{9},{10},{11},{12},{13},{14},{15},{16},{17},{18},{19},{20}}；

U/IND(A-{x1})={{1},{2},{3},{4},{5},{6},{7},{8},{9,14},{10},{11},{12},{13},{15},{16},{17},{18},{19},{20}}≠U/IND(A)；

U/IND(A-{x2})={{1},{2},{3},{4,8},{5},{6},{7},{9},{10},{11},{13},{15},{16},{17},{18},{19},{20}}≠U/IND(A)；

…

U/IND(A-{x6})={{1},{2},{3},{4},{5},{6},{7},{8},{9},{10},{11},{12},{13},{14},{15},{16},{17},{18},{19},{20}}=U/IND(A)

…

同理可以依次计算。所以，属性x6是可省的，而其他指标不可省。这样就把原来的22个指标简化为15个，即x1,x2,x3,x4,x7,x8,x9,x10,x12,x13,x14,x15,x18,x19,x22。

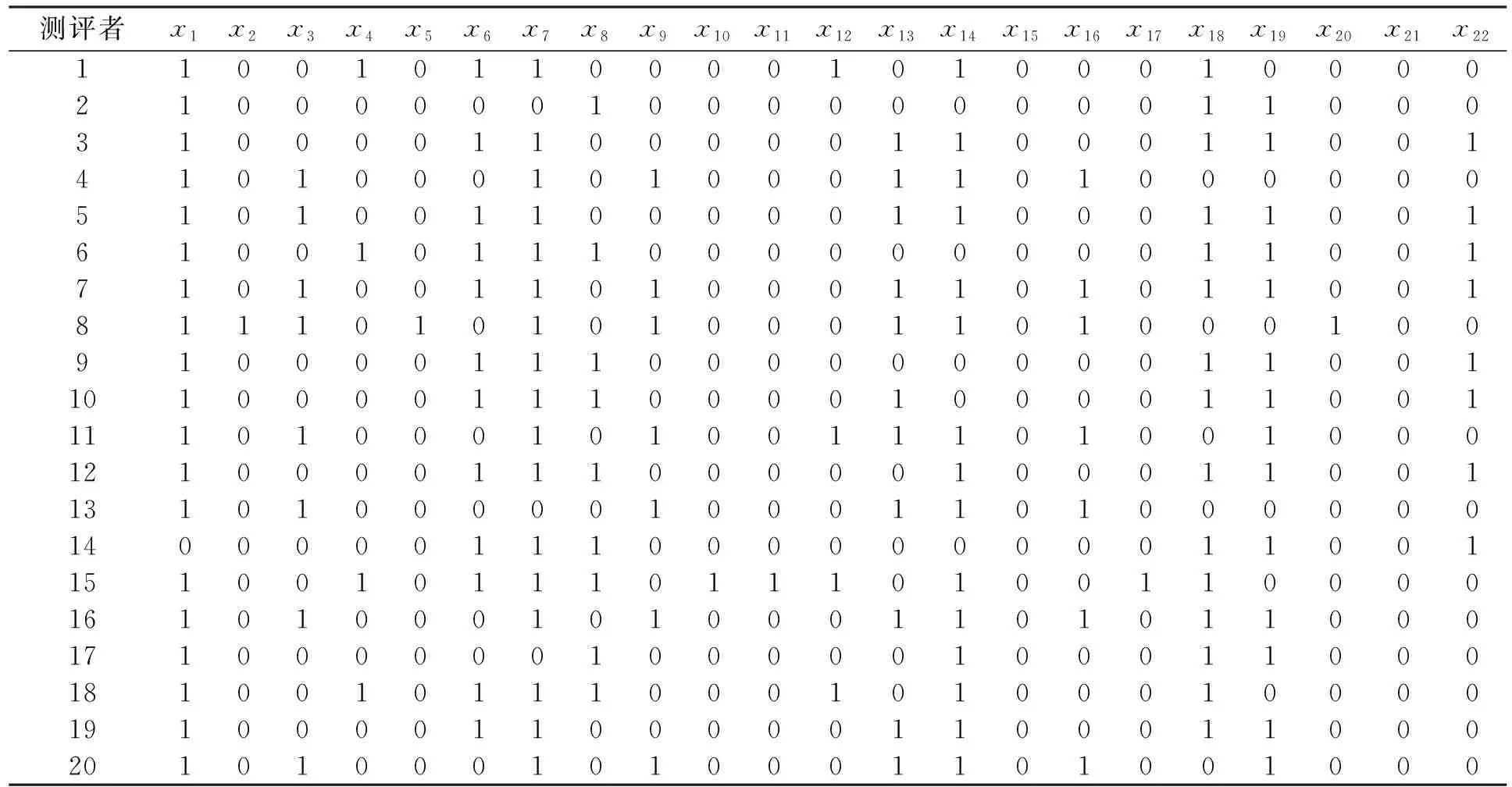
表3 评价指标信息

2.2 基于PCA的主成分提取

为了将RS处理后的指标顺序条理化，将筛选后的15个指标重新标号如表4：

A={x1,x2,x3,x4,x7,x8,x9,x10,x12,x13,x14,x15,x18,x19,x22}

={x1′,x2′,x3′,x4′,x5′,x6′,x7′,x8′,x9′,x10′,x11′,x12′,x13′,x14′,x15′}

将筛选后的样本数据(SPSS软件处理数据时自动标准化，因此无需进行这一步骤)，运用软件SPSS17.0进行数据处理，可得相关系数矩阵R的特征值和方差贡献率以及累积方差贡献率，见表5。在结合实际情况下，根据累计方差贡献率达到85%规定或根据特征值大于1选取主成分的个数(本文取特征值大于1作为主成分)，并记选取主成分为：Y1,Y2,…,Yg。

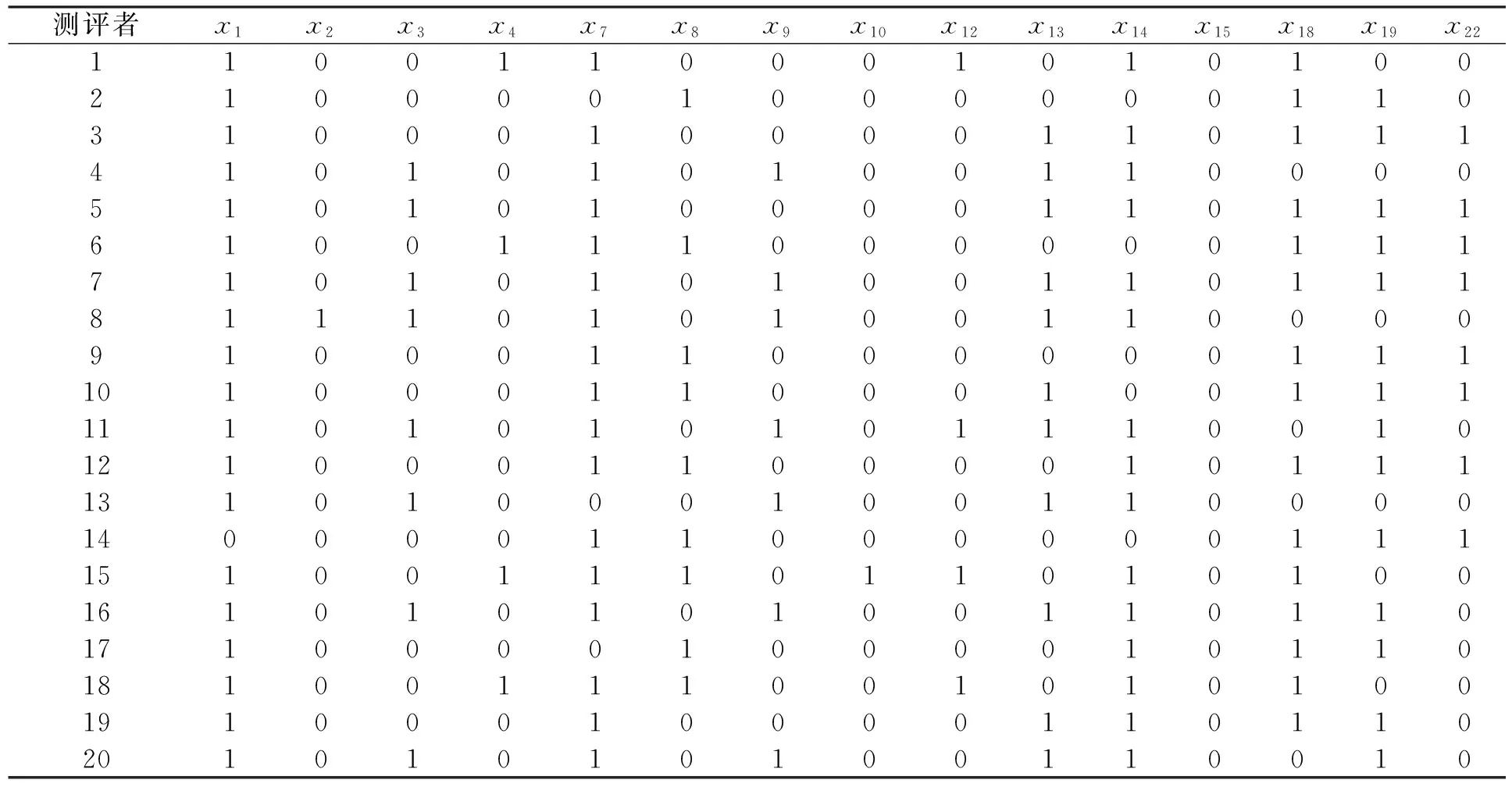
表4 初步约简评价指标信息

根据表5，得到主成分个数g=6，此时方差累计贡献率为86.397%，六个主成分包含了绝大部分信息。因此，可得6个主成分表达式：

Y1=0.387·x1′+0.327·x2′+…+0.178·x13′+0.037·x14′-0.119·x15′

Y2=0.095·x1′+0.093·x2′+…-0.080·x13′-0.370·x14′+0.057·x15′

…

Y6=0.045·x1′-0.215·x2′+…+0.195·x13′-0.275·x14′+0.745·x15′

根据上述六个主成分的表达式，并比较表5中uij的绝对值，其值大小说明各因素对六大主成分影响程度的大小，对六个主成分中各影响因素重新定义归类，其各主成分所反应的含义如下：

表5 相关系数矩阵R的特征值、方差贡献率、累计方差贡献率和对应的特征向量

(1)第一主成分Y1主要反应了管理者的管理和技术水平因素、施工人员的素质和理论水平因素等，可以归结为项目参与者工作质量保障程度；

(2)第二主成分Y2主要反应了工程项目规模、标准及配套设施因素和业主与用户需求的质量特性与指标要求等，可以归结为项目规模和品质要求；

(3)第三主成分Y3主要反应了工程项目工期长短的因素和施工技术的障碍、难题等，可以归结为项目弹性水平；

(4)第四主成分Y4主要反应了工程款拖欠程度和施工组织的合理性等，可以归结为项目组织及资金分配合理性；

(5)第五主成分Y5主要反应了机械设备的合理选择与使用情况和技术、管理和自然等环境变化的干扰等，可归结为项目外界特殊干扰承受能力；

(6)第六主成分Y6主要反应了自然灾害、罢工、战争等不可抗力等因素，可以归结为项目抗风险能力。

2.3 评价模型构建

根据上述分析，得到了6个主成分。设F为综合评价函数，可得：

F=α1Y1+α2Y2+…+αgYg

其中，α1,α2,…,αg是主成分Y1,Y2,…,Yg的方差贡献率，体现主成分在综合评价函数F值大小上的影响程度。F表示大型工程质量、工期和费用综合集成化评价模型，对样本中的综合评价函数值按大小排序，从而可得出各样本综合评价得分排名。

由表5中的方差贡献率α1,α2,…,αg和已求得的六大主成分Y1,Y2,…,Y6，代入上式，得到大型工程项目三大目标综合评价函数：

F=0.276Y1+0.180Y2+0.155Y3+0.102Y4

+0.083Y5+0.068Y6

综合函数F表示大型工程项目三大目标集成化的评价模型，代入标准化后的数据，计算各被测评者的得分，得出排序结果，见表6，进而可以进一步进行动态化分析。

3 评价结果的集成化动态分析

根据表6，不但可以看出筛选后的影响大型工程项目质量、工期和费用三大目标的15个因素经过降维处理而形成的六个主成分的得分排名，而且还能得出六大主成分对综合评价函数影响程度的大小，便于项目决策者做出合理的决策。具体可得如下分析结果：

(1)由Y1,Y2,…,Y6的排名，可以分别得出影响项目参与者工作质量保障程度、项目规模和品质要求、项目弹性水平、项目组织及资金分配合理性、项目外界特殊干扰承受能力和项目抗风险能力因素程度的大小，进而针对某方面存在的可改进之处，分别从质量、工期和费用方面进行决策来提高大型工程项目管理的合理性。

(2)对比Y1,Y2,…,Y6主成分得分排名和综合评价得分排名，可以发现综合得分最高但是Y5却排名16，Y1、Y4、Y6排名第6，而并不是六个主成分得分都是最高。因此，Y1和Y2主成分可以归纳到质量相关方面，Y3和Y4主成分可以归纳到费用相关方面，Y5和Y6主成分可以归纳到工期相关方面，通过表6可以发现，要提高Y5(Y6)则必然会影响到Y1(Y2)和Y3(Y4)，对比综合评价函数得分的排名可以得出：

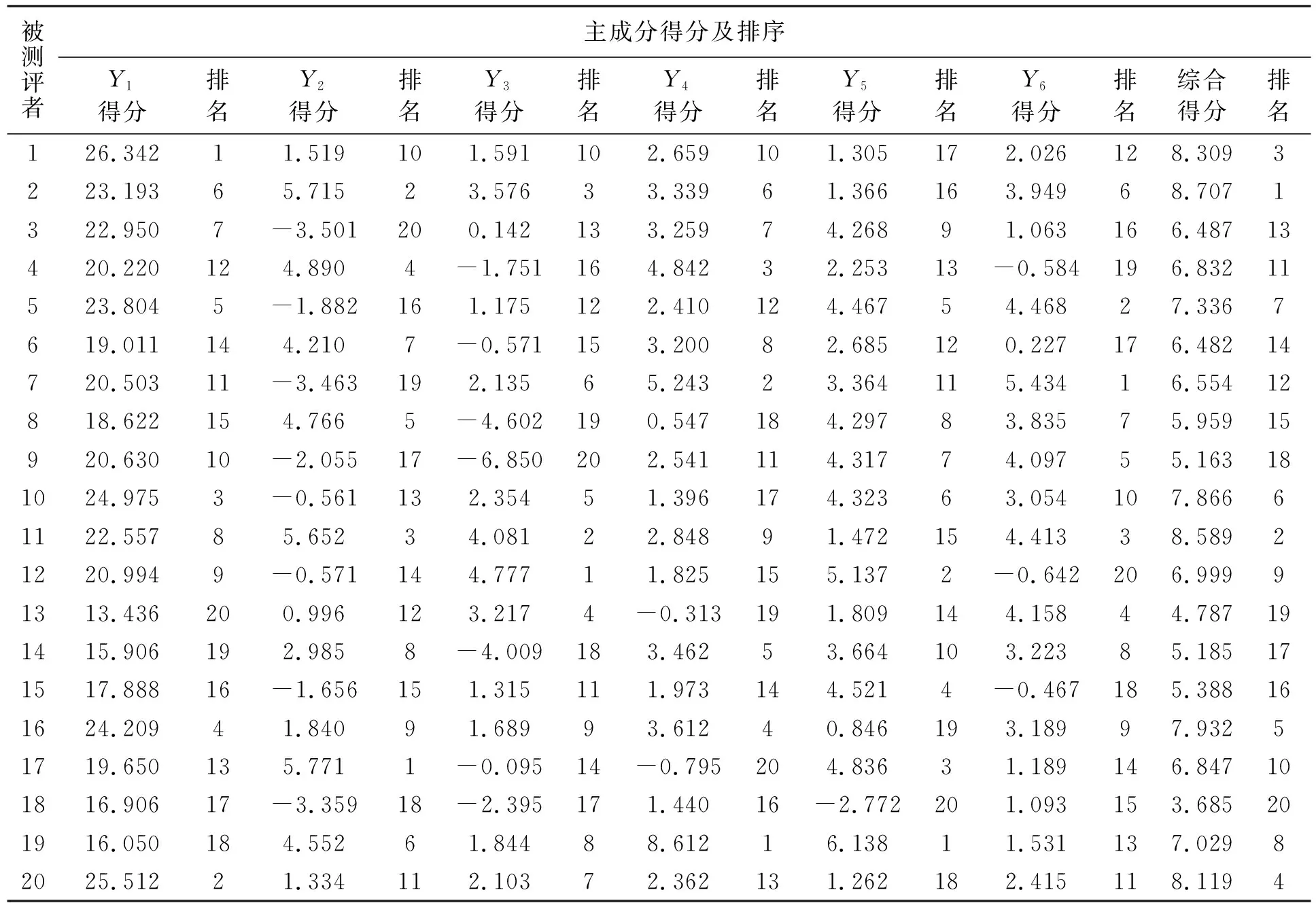
表6 主成分排名和综合评价得分排名

a.若要提高大型工程项目质量，则会增加费用，可能延长工期；

b.若要缩短大型工程项目工期，则会增加费用，可能会降低质量；

c.若要减少大型工程项目费用，则会降低质量，延长工期。

这是一种集成化的动态不平衡关系，因项目不可能实现质量最好、费用最低、工期最短三大目标分别都处于最佳状态，而只能是满足一种最优化平衡状态，即在追求质量(费用或工期)的同时，控制费用和工期(质量和工期或质量和费用)，使之处在相对更合理的平衡状态上。

若Y5(Y6)为主要目标，Y1(Y2)作为次级目标，为达到项目目标平衡化，则必须对Y3(Y4)目标进行稍大程度地调整，对次级目标Y1(Y2)做小幅调整，根据分项指标对一级目标的影响程度值评分表，调整各指标评分值，即对该影响因素进行改善措施，并可根据调整后得分的排名情况进行判断。同理，Y1(Y2)或Y3(Y4)作为主要目标时，处理方式类同。而上述所得出的3种可能结果，也正符合实际大型工程项目管理中可能出现的状况。

4 结 语

大型工程往往是一个较复杂工程或复杂工程，影响其质量、费用和工期的因素有很多，因此通过RS理论来删除冗余指标，再结合统计学中的PCA来对多个影响因素进行降维处理，从而可以获取大型工程三控目标的主要知识信息。将筛选后得出的主成分进行深入分析、重新归类处理，计算主成分得分与综合评价函数得分并将其各自得分排名进行对比，通过动态思维的视角对大型工程质量、费用与工期进行集成化动态分析，得出符合实际大型工程项目管理中的可能结果。

通过算例分析表明，基于RS和PCA得出的大型工程目标集成化综合评价函数得分值与各主成分的得分值，并依此而排序所进行的动态分析能得到较好的应用。因此，根据大型工程质量、费用和工期三大管理目标之间隐含的这种此消彼长的关系来进行最优化决策，便于项目管理更趋于合理性，有助于项目管理者做好更科学的决策，从而提高大型工程项目管理的效益。

[1] 陈东方，陈建国．建设工程进度预警及其模型构建的研究与应用[J]．工程管理学报，2010，24(3)：318-322.

[2] 张 浩，吴炜煜．基于合约事务的工程项目费用管理[J]．清华大学学报(自然科学版)，2005，45(3)：293-296.

[3] 熊 鹰，匡亚萍．基于蚁群算法的施工项目工期-成本优化[J]．系统工程理论与实践，2007，(3)：105-111.

[4] 吴二军，黄 俊，郭 建，等．建筑物整体平移新技术施工中的质量管理和工期管理[J]．建筑管理现代化，2003，(1)：40-42.

[5] 张增群，王 毅，杨志明．建筑工程设计质量寿命和费用评价模型研究[J]．建筑设计管理，2007，(1)：39-40.

[6] 张文修，吴伟志．粗糙集理论介绍和研究综述[J]．模糊系统与数学，2000，14(4)：1-12.

[7] Pawlak Z．Rough set theory and its applications to data analysis[J]．Cybernetics and Systems, 1998，29(1)：661-688.

[8] 李龙俯，程慧霞，卢冰原．基于凸Rough集的数据约简和规则发现研究[J]．东南大学学报，2002，32(2)：201-206.

[9] 格里菲思，斯蒂芬森，沃森.工程建设项目管理体系[M].李世蓉，陈君薇，虞向科，等译.重庆：重庆大学出版社，2006.

[10]王春峰，万海晖，张 维．商业银行信用风险评估及其实证研究[J]．管理科学学报，1998，1(1)：68-72.