应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估*

潘文超

(中国科技大学 企业管理系，台湾 台北 104)

一、前言

近年来，优化问题处理已经逐渐受到重视，例如物流业的最短路线问题[1]或是交通运输业的排班问题[2]等，都必须经由优化算法来加以处理。到目前为止，经常被用来处理优化问题的算法包括了遗传算法[3]与粒子群算法[4]。然而，这些算法的共同缺点就是计算过程复杂且初学者不容易了解。

有鉴于此，本文不同于以往学者，而是采用一种全新的果蝇优化算法(Fruit Fly Optimization Algorithm，简称FOA)。这种优化算法具有计算过程简单，容易将它的观念转换为程序代码而且非常容易理解等优点。本文首先尝试以求得函数极大值的方式，测试此优化算法的功能；然后，进一步的按照财务五力中的活动力、安定力与收益力搜集台湾2008、2009年企业财务比率资料，根据活动力、安定力与收益力进行灰关联分析，再将二者的分析结果，按照灰关联度进行排序，以了解各企业的经营绩效排名，并且以二分法的方式分为绩效好与坏二类，然后以财务比率作为自变量(X)，以绩效好坏作为因变量(Y)，再采用三种数据探勘技术，包括果蝇优化算法优化广义回归神经网络(Fruit Fly Optimization Algorithm optimized General Regression Neural Network，简称 FOAGRNN)、一般广义回归神经网络(General Regression Neural Network，简称 GRNN)与多元回归模型(Multiple Regression，简称 MR)，进行企业经营绩效侦测模型的建构，以供研究人员参考。

本文主要的结构是：第一节介绍研究动机与目的，第二节介绍果蝇优化算法与探讨以求解极大值为范例，第三节介绍所使用的样本数据与实际案例分析，第四节提出研究结论与建议。

二、果蝇优化算法

果蝇优化算法是由笔者提出[5，6]，一种基于果蝇觅食行为推演出的寻求全局优化的新方法。果蝇本身在感官知觉上优于其他物种，尤其是在嗅觉与视觉上。果蝇的嗅觉器官能很好地搜集飘浮在空气中的各种气味，然后飞近食物位置后亦可使用敏锐的视觉发现食物与同伴聚集的位置，并且往该方向飞去。

依照果蝇搜寻食物的特性，将其归纳为几个必要的步骤与程序范例，以提供读者参考。如图1。

图1 果蝇群体迭代搜索食物示意图

1.随机初始果蝇群体位置(Fly Group)。

Init X_axis；Init Y_axis.

2.赋与果蝇个体(Fly1，Fly2，Fly3)利用嗅觉搜寻食物之随机方向与距离。

Xi= X_axis + Random Value.

Yi= Y_axis + Random Value.

3.由于无法得知食物位置，因此先估计与原点之距离(Dist)，再计算味道浓度判定值(S)，此值为距离之倒数。

4.味道浓度判定值(S)代入味道浓度判定函数(或称为Fitness function)以求出该果蝇个体位置的味道浓度(Smelli)。

Smelli=Function(Si).

5.找出此果蝇群体中的味道浓度最高的果蝇(求极大值，例如Fly2)。

[bestSmell bestIndex] = max(Smell).

6.保留最佳味道浓度值与x、y坐标，此时果蝇群体利用视觉向该位置(Fly2)飞去，形成新的群聚位置。

Smellbest = bestSmell.

X_axis = X(bestIndex).

Y_axis = Y(bestIndex).

7.进入果蝇迭代寻优，重复执行步骤2-5，并判断味道浓度是否优于前一迭代味道浓度，若是则执行步骤6。[注]其完整程序代码，可以参考网址：http：//www.oitecshop.byethost16.com/FOA.html，2011-11-07.

本文尝试以FOA求得极大值，其函数为Y=3-X2，此极大值的解答为3。随机初始化果蝇群体位置区间为[0，10]，迭代的果蝇搜寻食物的随机飞行方向与距离区间为[-1，1]。经由100次迭代搜寻最大值后，程序执行结果逐渐逼近该函数极值之解答。图2为迭代搜寻函数极值的解所绘制的曲线图，由图中可发现该曲线逐渐逼近函数极大值3，而该群果蝇之坐标为(80.329 6，74.335 1)。

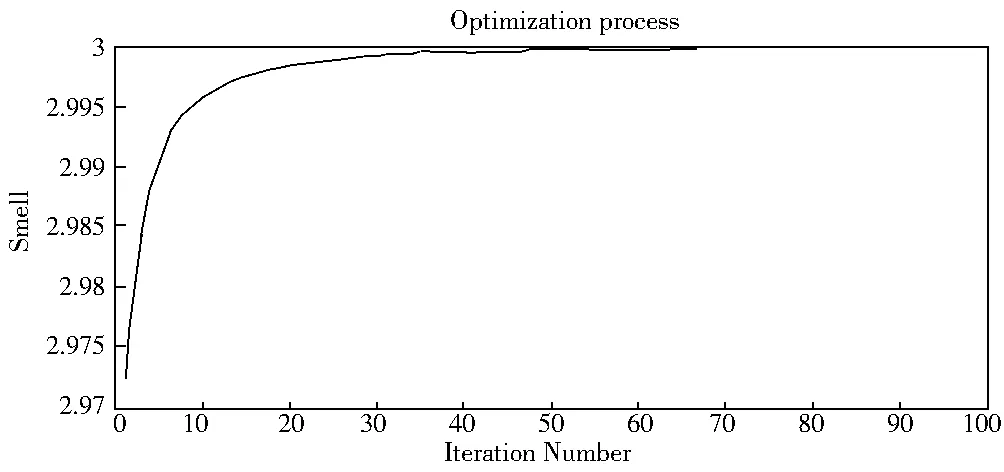
图2 迭代搜寻函数极值曲线图

三、案例分析

(一)样本数据与变量

本文自台湾情报赢家数据库搜集2008年及2009年1 000家上市上柜公司财务比率数据作为自变量。这些财务比率资料是依据财务五力中的活动力 (应收账款周转率X1，资产周转率X2，股东权益周转率X3)，安定力 (流动比率X4，速动比率X5，负债比率X6) 和收益力(毛利率X7，营业利益率X8，纯益率X9)等三力所搜集，这些财务比率的叙述统计值，如表1所示。

表1 台湾1 000家公司的财务比率叙述统计值

(二)企业的经营管理绩效分析

本文采用Tong的方法使用财务比率作为评价因子[7]，然后利用Deng教授提出的灰关联分析并且使用Wenetal.教授所开发的灰关联分析 Matlab 工具箱去分析1 000家企业的灰关联度值并进行排名[8，9]。此外，本文选择负债比率最小值，其余比率最大值做标准序列。根据灰关联的定义，灰关联度是二条序列之间的相关程度。不同的比较序列与标准序列会产生相应的灰关联度再将其排序为灰关联序。越高的灰关联度值代表其企业的经营绩效越佳。因此，选取前500名企业经营绩效佳的上市上柜公司(以0表示) 和后500名企业经营绩效不佳的上市上柜公司(以1表示)作为因变量(Y)。本文采用MATLAB7.0 软件进行灰关联分析，而图3中各序列分别代表一家台湾上市上柜公司；一条序列中共有9个节点，分别代表9种形态的财务比率，用星号线连接称为标准序列(Standard sequence)，其余的线称为比较序列(Inspected sequence)。若比较序列越接近标准序列，代表该企业的经营绩效越好。研究发现，在2008年的企业中经营绩效前3名的企业分别是关贸(6 183)、 思源(2 473)和景岳(3 164)，而经营绩效后3名的企业分别是美嘉电(4 415)、得捷(5 204)和陇华(2 424)；在2009年的企业中经营绩效前3名的企业分别是关贸(6 183)、大冢(3 570)和通泰(5 487)，而经营绩效后3名的企业分别是茂德(5 387)、佳鼎(5 318)和建台(1 107)。本文将财务比率自变量与因变量作为样本数据共有1 000笔，并且将此1 000笔数据区分为5小组，然后以4小组数据进行模型建构，1小组数据进行模型测试的方式作交叉验证(Cross-testing)，以验证企业经营绩效侦测模型的稳定性。

(三)建构三种企业经营绩效侦测模型与比较分析

本文将1 000笔样本数据进行正规化，使样本介于0到1之间，然后细分为5小组，以4小组数据作为训练数据建构模型，1小组数据作为测试数据测试模型稳定性的方式进行交互验证。将三种模型的输出结果定义为小于或等于0.5归类为0(也就是经营绩效佳)，大于0.5归类为1(也就是经营绩效不佳)。首先利用前4小组训练数据分别建构FOAGRNN、一般GRNN与传统多元回归等三种模型，有关GRNN的理论，读者可参考Specht教授的相关著作[10，11]。在FOAGRNN模型方面，本文采用GRNN matlab 工具箱并自行撰写MATLAB程序，设计FOA动态搜寻最佳GRNN的Spread参数值，建构FOAGRNN模型。GRNN的Spread参数初始值设定在[0.001，1]之间，网络输入层神经元为9个、输出神经元为1个。

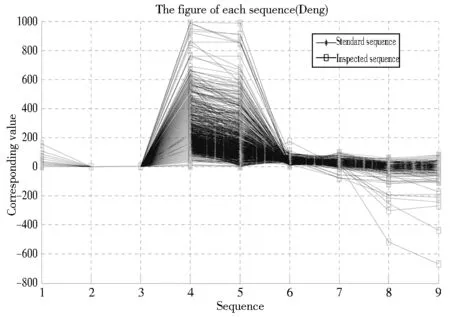
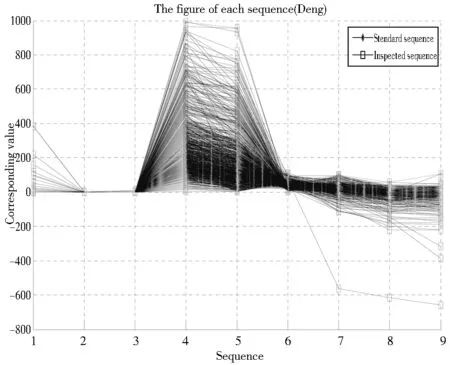
图3 灰关联分析之线性序列图

在FOA初始参数的设定方面，随机初始化果蝇群体位置区间为[0，100]，迭代之果蝇搜寻食物的随机飞行方向与距离区间为[-10，10]，果蝇种群规模大小为20只，迭代(iterative)次数为100。FOA优化GRNN的做法是先计算出果蝇个体位置与原点坐标(0，0)之间的距离并计算倒数，以求出味道浓度判定值(S)，再将它代入GRNN的参数Spread内，输入训练数据得出网络输出值，再与目标值计算出RMSE(或称为Fitness)，此值越小越好，保留最好的味道浓度判定值(S)作为GRNN之Spread值，依此方法进行迭代搜寻。透过果蝇的嗅觉随机觅食，再透过视觉而聚群在香味最浓的位置，可将GRNN的Spread参数值调整到最佳值，使网络输出值与目标值两者之间的RMSE调整到最小。此外，一般GRNN之Spread值则采用默认值1进行建模，最后再以SPSS进行多元回归模型的建构。

图4上方2个图形分别代表2008及2009年第1小组训练资料，以FOA迭代优化GRNN的Spread值，产生的输出值与目标值之间的RMSE。经过100次迭代演化后，2008年在第19代开始收敛，坐标为(35.442 6，27.266 0)，Spread值及RMSE值分别为[0.012 3，0.006 5]；2009年在第17代开始收敛，坐标为(33.668 3，22.550 2)，Spread值及RMSE值分别为[0.012 6，0.011 5]。然而，图4下方2个图形分别代表2008及2009年样本数据以4小组数据作为训练数据建构模型，1小组数据作为测试数据，进行交互验证FOAGRNN、一般GRNN与传统多元回归等三种模型产生之结果数据，将它们绘制而成ROC曲线图。Bradley指出参考线与曲线下的面积愈大[12]，代表该模型分类能力愈准确。由图4中可以明显看出，FOAGRNN模型的曲线下的面积(AUC)最大，因此分类能力最好。再由表2观察ROC曲线分析之输出结果，其中敏感度(Sensitivity，Sen)是指预测结果为1(亦即经营绩效不佳)的个数占实际值为1的个数的百分比，明确度(Specificity，Spe)是指预测结果为0(亦即经营绩效佳)的个数占实际值为0的个数的百分比，而Hand教授指出吉尼系数(Gini Index) 等于 2倍的AUC减1[13]。由于这些指标值皆愈大愈好，表2中2008年的FOAGRNN模型的明确度为0.928、敏感度为0.906、曲线下的面积为0.917与吉尼系数为0.834，而2009年的FOAGRNN模型的明确度为0.904、敏感度为0.886、曲线下的面积为0.895与吉尼系数为0.790，皆高于一般GRNN与传统多元回归模型，因此FOAGRNN模型有很好的分类预测能力。

图4 FOAGRNN搜寻优化参数之迭代RMSE趋势及分类预测结果之ROC曲线图

ModelSenSpeAucGini2008FOAGRNN0.9280.9060.9170.834GRNN0.8120.8020.8070.614MR0.8020.6200.7110.4222009FOAGRNN0.9040.8860.8950.790GRNN0.8180.7840.8010.602MR0.8160.6720.7440.488

四、结论

在本文中，不同于传统财务预警模型的建构方法，以二分法的方式区分为企业经营绩效佳与企业经营绩效差二类，同时结合财务比率作为样本数据进行三种企业经营绩效侦测模型建构，包括了果蝇优化算法优化广义回归神经网络、一般广义回归神经网络与多元回归模型，研究结果如下。

1.经由果蝇优化算法迭代动态调整广义回归神经网络的spread参数值之后，RMSE收敛值可以降低，分类预测能力可以明显提升。

2.经由果蝇优化算法调整广义回归神经网络其分类预测能力与稳定性，明显优于一般广义回归神经网络和多元回归模型。

此外，提出一种新的FOA，并实际应用于求解极大值。经测试结果发现，FOA皆能顺利求出解答，此算法不仅具备了简单易懂的特色，更容易将它撰写成程序代码，并且程序代码相较于遗传算法[14]和粒子群优化算法[15]，不会太过冗长，容易拿来处理各种优化问题。

参考文献：

[1] Hart，P E，Nilsson，N J and Raphael，B.A formal basis for the heuristic determination of minimum cost paths[J]. IEEE Transactions on Systems Science and Cybernetics SSC4，1968(2)：100-107.

[2] Friedman，M.A mathematical programming model for optimal scheduling for buses depature under deterministic condition[J].Transportation Research，1976，10(2)：83-90.

[3] Gupta，Y P，Gupta，M C，Kumar，A and Sundram，C.A genetic algorithm-based approach to cell composition and layout design problems[J].Int.Journal of Production Research，1996，34(2)：447-482.

[4] Yan，S Y，Lee W T and Shih，Y L.A path-based analogous particle swarm optimization algorithm for minimum cost network flow problems with concave arc costs[J].Transportation Planning Journal，2007，36(3)：393-424.

[5] Pan，W T.A new evolutionary computation approach：Fruit Fly Optimization Algorithm[C].2011 Conference of Digital Technology and innovation Management Taipei,2011.

[6] Pan，W T.A new fruit fly optimization algorithm：Taking the financial distress model as an example[J].Knowledge-Based Systems，In Press，2011.

[7] Tong，L L and Shih，B C.Predict the financial crisis by using grey relation analysis，neural network，and case-based reasoning[J].Chinese.Manage Rev，2011，4(2)：25-37.

[8] Deng，J.The control problems of grey system[J].System & Control Letters，1982(5)：288-294.

[9] Wen，K L，Chang Chien S K.，Yeah C K，Wang，C W and Lin H S.Apply matlab in grey system theory[M].Chuan Hwa Book Co.Ltd，Taiwan，2006.

[10] Specht，D.F.Probabilistic neural networks and the polynomial adaline as complementary techniques for classification[J].IEEE Trans.on Neural Networks，1990，1(1)：111-121.

[11] Specht，D F.A general regression neural network[J].IEEE Tras.Neural Networks，1991，2(6)：568-576.

[12] Bradley，A P.The use of the area under the ROC curve in the evaluation of machine learning algorithms[J].Pattern Recognit，1997，30(7)：1145-1159.

[13] Hand，D J and Till，R J.A simple generalisation of the area under the ROC curve to multiple class classification problems[J].Mach Learn，2001，45(2)：171-186.

[14] Holland，J.Adaptation in natural and artificial systems[M].MIT Press，Cambridge，1992.

[15] Eberhart，R C and Kennedy J.new optimizer using particle swarm theory[C].Proc，Sixth International Symposium on Nagoya，Japan，1995：39-43.