应用边界元模拟方法分析复杂海底地震散射特征*
李绪宣 于更新 符力耘 温书亮 管西竹
(1.中海油研究总院; 2.中国科学院地质与地球物理研究所)
应用边界元模拟方法分析复杂海底地震散射特征*
李绪宣1于更新2符力耘2温书亮1管西竹2
(1.中海油研究总院; 2.中国科学院地质与地球物理研究所)
边界元法对随机起伏的复杂海底界面具有良好的适应性。比较了边界元法与有限差分法对复杂断层模型的模拟精度,并验证了边界元法的有效性。利用边界元法对复杂海底模型进行波场模拟,反映起伏海底界面对地震波传播的影响;利用统计参数描述复杂海底地貌特征,将崎岖海底界面划分为快、慢变化和强、弱起伏等4种特征类型。根据不同统计参数的选择建立崎岖海底理论模型,利用边界元法对不同类型的崎岖海底理论模型进行模拟研究,同时与实际海底资料相对比,分析了复杂海底地震散射特征。此项研究成果可为复杂海底地区目标导向地震观测系统设计和采集参数优化提供理论依据。
边界元法 复杂海底 地震波传播 散射特征
深水海底地貌和结构复杂,而地震勘探观测一般是在水面进行,因此深刻理解地震波在复杂海底地貌和结构上的散射特征对于地震采集观测具有重要的应用价值。边界元法是继有限元法发展起来的一种数值模拟方法,已在过去几十年里得到了广泛的研究和发展[1-11]。由于边界元法只在研究区域的边界上剖分单元,因而将求解问题的维数降低,大大减少了所要求解的节点数,显著提高了计算效率。该方法的特点是:①自动满足无穷远处边界条件,适于无限域问题;②在几何上精确描述地下不规则界面;③显式应用地下界面的连续边界条件;④可分别模拟来自地下不同部位的波。因此,笔者认为边界元法对随机起伏的复杂界面有着良好的适应性,非常适用于复杂海底地貌和构造的地震波正演模拟。
本文利用边界元法对复杂海底模型进行波场模拟,反映起伏海底界面对地震波传播的影响;并将边界元法与有限差分法相对比,验证了边界元法的有效性;使用统计参数描述复杂海底地貌的统计特征,将崎岖海底界面划分为快、慢变化和强、弱起伏等4种特征类型;根据不同统计参数的选择建立崎岖海底理论模型,应用边界元法对不同类型的崎岖海底理论模型进行模拟研究,同时与实际海底资料相对比,定量分析了复杂海底地震散射特征。此项研究可为复杂海底地区目标导向地震观测系统设计和采集参数优化提供理论依据。
1 边界元模拟方法
1.1 边界积分方程及其离散
图1所示为一起伏海底模型,由Ω0和Ω12个子域组成,子域Ω0的上下边界分别以Γ0和Γ1表示,子域Ω1由边界Γ1和无穷远处边界表示,且假定其两端趋于无穷。界面Γ0为自由水面,震源位于子域Ω0内(为简化起见,这里只讨论二维声波问题),则子域Ω0内的地震波响应u(r)满足边界积分方程

式(1)中:Γ为边界,Γ=Γ0+Γ1;u0(r)为入射场,u0(r)=S(ω)G(r,r0);∂/∂n 表示边界 Γ 外法向导数:r为源节点的位置矢量;r′为易节点的位置矢量;G(r,r′)表示均匀背景介质空间的格林函数,对于二维问题,可表示为
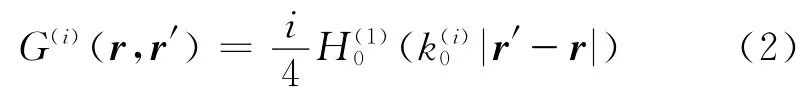

图1 起伏海底模型示意图
对式(1)应用自由水面应力为零的条件,则得到
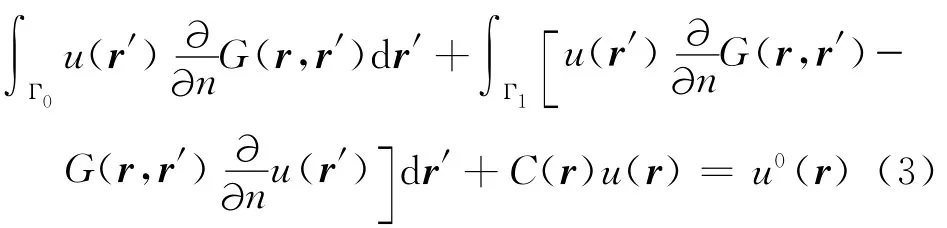
对于子域Ω1,无穷远处边界上位移和应力满足远场辐射条件,即
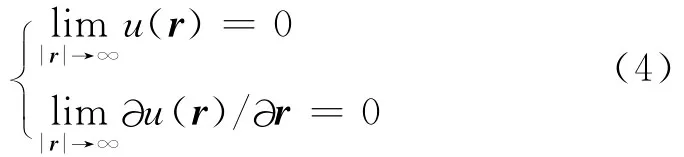
则其对应边界积分方程为

在Ω0与Ω1之间的公共界面上Γ1位移和应力连续,即
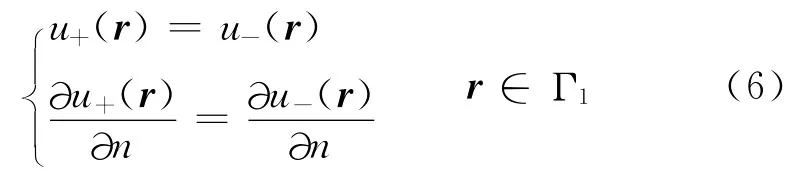
式(6)中:u+(r)为边界Γ1上界面的位移;u-(r)为边界Γ1下界面的位移。
为了求解积分方程,首先要对边界Γ进行离散。将边界Γ划分为L个边界元,记为Γe(e=1,2,…,L),总节点数为N。假设小单元Γe由节点I1、I2所确定,利用插值形函数φ,变量r、u和∂u/∂n即可由节点上相应变量值的线性组合来近似,以u为例:
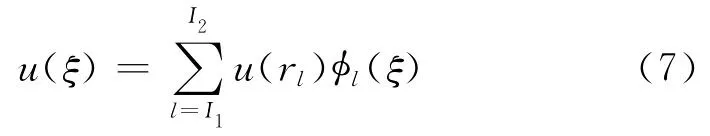
其中ξ为一个单元的局部坐标。
将方程(1)写为算子形式:

式(8)中:H、G为边界积分算子;f为入射波场;u为边界上的位移;t为u在边界上的法向导数,t=∂u/∂n。边界积分算子H和G的离散形式可分别表示为

其中δij为Kronecker delta函数。这些积分可由高斯积分数值算法计算得出。在每个子域按式(8)建立方程,则可得到对应的总体矩阵方程组,利用高斯消去法求解此线性方程组,即可求得模型中所有节点的地震响应u(r)。
1.2 改进算法
为提高算法的效率,我们采用了改进的分块高斯消去法来求解矩阵方程。在海上勘探中,震源和检波器均位于海水表层,所以仅需计算自由水面的地震响应。采用由深至浅的方式逐层进行边界系数矩阵的数值计算、组装和消元,消去2个相邻子域公共边界上的耦合数据,如此计算至水层,得到最后的矩阵方程,其维数仅由水层的节点数确定。将此矩阵与多测线多震源相结合,可计算出水面任意处的观测波场。在整个计算过程中,主矩阵需要的最大内存仅由最大子域的总节点数确定,这样既节省了内存又缩短了计算时间。
为了提高计算效率,在程序执行中采用了一种变单元尺寸的方法。由于单位波长3个单元采样足以确保结果的精度,而波长是频率的函数,所以程序可根据介质速度和每一个计算频率自动计算出相应的单元尺寸并自动剖分单元,从而提高了计算速度并使参数输入简化。对于存在人工边界的子域,引入无限元吸收边界[12]可使模型截断边界的散射最小化。与传统吸收边界条件方法相比,此方法不仅有效改善了吸收效果,而且节省了存储空间和运算时间。
1.3 有效性验证
为了验证边界元法对复杂海底地貌模型的正确性和有效性,首先设计了一个复杂断层模型,模型尺寸为3800 m×1500 m,各层层速度如图2a所示,计算频率为0~40 Hz。分别使用边界元法与有限差分法对该模型进行数值模拟,对比边界元法模拟结果(图2b)与有限差分法模拟结果(图2c),可以看出两者具有较好的一致性;但边界元法可以清晰地刻画出断层各断点的绕射,而有限差分法的模拟结果中各断点的绕射则相对较弱。
为了进一步验证边界元法的模拟精度,分析该方法在崎岖海底模拟中的主要优势,又设计了一个起伏海底的二维速度模型进行模拟,各层层速度如图3a所示。该复杂海底模型大小为3000 m×2000 m,炮点位于(1500 m,0 m)处,计算频率为0~40 Hz。图3b—d分别为550、750和900 ms时刻计算的波场快照,可以看出模拟结果比较清晰地反映出了起伏海底界面对地震波传播的影响。

图2 设计的复杂断层模型及其自激自收剖面

图3 复杂海底地貌二维速度模型及其不同时刻的波场快照
根据对上述2个模型的模拟可以看出,边界元法能高效准确地模拟地震波在复杂地质构造中的传播,精确描述各层界面,准确反映各层间的波阻抗差异及地层厚度的变化,有效处理起伏界面引起的地震波散射,因此对崎岖海底模型的数值模拟具有明显的优势。
2 复杂海底地震散射特征分析
为了研究复杂海底地貌对地震波传播的影响,建立了崎岖海底理论模型和实际模型,并分别对2类模型进行边界元地震数值模拟,对地震波的传播散射特征进行了定量分析。
一个随机起伏的海底界面可以由不同的统计参数来描述。均方根高用来描述一条曲线或者一个表面的平均起伏高度,可以用来表征一个界面的崎岖程度。设界面高度分布函数为h(r),其中h为界面距离参考界面的高度,r为参考界面上点的位矢,则此界面的均方根高为相关长度用来描述一条曲线或者一个表面的起伏频率,可以用来表征一个界面的崎岖程度变化的频率,其计算公式为C(r)=〈h(r′)h(r′+r)〉/σ2,式中〈h(r′)h(r′+r)〉表示自相关,σ2为归一化因子。利用均方根高和相关长度这2个统计参数可以得到不同的随机起伏海底模型。图4a为一组均方根高相同、相关长度不同的随机起伏界面,其均方根高d为20 m,相关长度a分别为22 m(细线)和220 m(粗线)。图4b为一组相关长度相同、均方根高不同产生的模型,其相关长度a为40 m,均方根高d分别为50 m(细线)和10 m(粗线)。从图4中可以看出:均方根高越大,其界面随机起伏程度越强;反之,均方根高越小,其界面随机起伏程度越弱。而相关长度越小,其界面起伏频率变化越快;反之,相关长度越大,其界面起伏频率变化越慢。
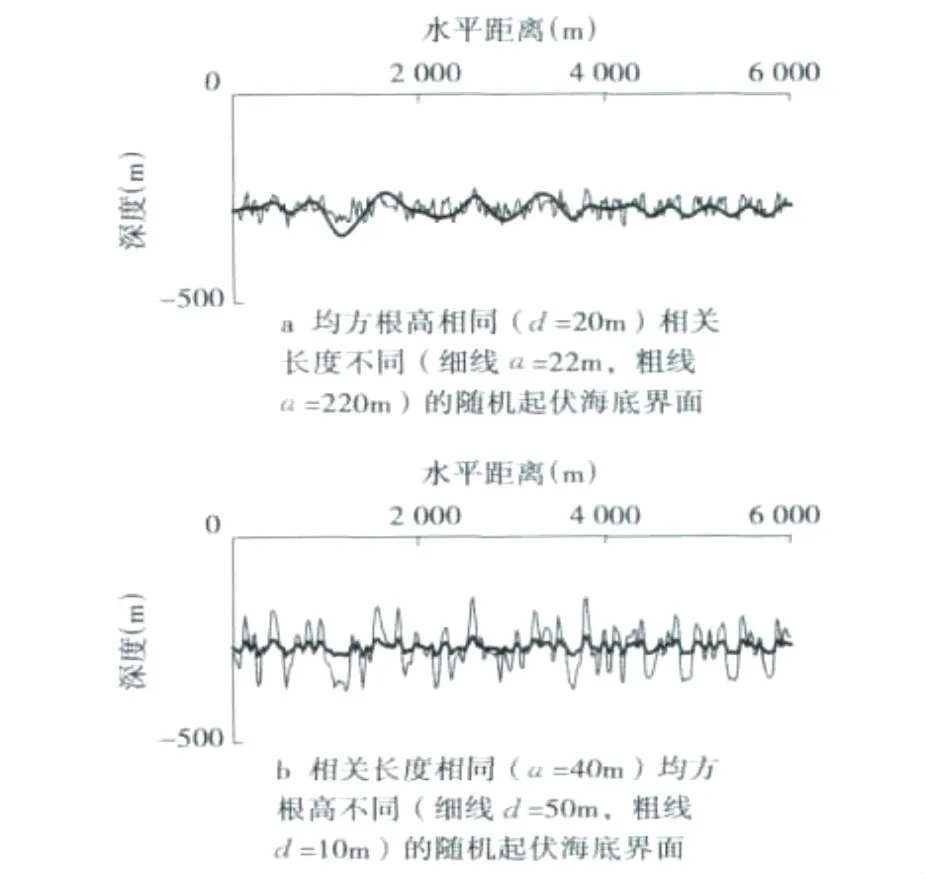
图4 随机起伏海底理论模型

图5 不同随机起伏海底模型的反射能量曲线(a、b)与反散射能量曲线(c、d)
分别使用以上4条曲线作为海底随机起伏界面进行数值模拟。设水层速度为1500 m/s,下伏地层速度为3000 m/s,炮点坐标为(0 m,0 m),计算频率为0~45 Hz,主频为20 Hz,利用对复杂海底理论模型的地震模拟结果可计算得到反射能量曲线(图5a、b)与反散射能量曲线(图5c、d)。反射能量曲线是通过对单炮记录所有频率分量总和进行计算得到,而反散射能量曲线则是利用归一化后的起伏海底模型的反射能量曲线与水平海底模型的反射能量曲线相减获得。由图5可知,能量曲线在水平距离大约为600 m处出现能量峰值,之后随偏移距增大而逐渐衰减。根据反射能量曲线变化可以看出,快变海底(相关长度小)反散射损失与慢变海底(相关长度大)反散射损失基本持平;强起伏海底(均方根高大)反散射损失大,而弱起伏海底(均方根高小)反散射损失较小。类似地,我们也计算了透散射能量曲线,其变化规律与反散射情况比较相似。对于强起伏快变化海底模型(均方根高大、相关长度小),地震波变化剧烈且与其复杂程度表现出一定的相关性,其透散射能量在近偏移距变化很大且随偏移距增大而快速衰减。为了分析起伏海底对不同频率的响应特征,我们将计算频率划分为低(0~25Hz)、中(26~50 Hz)、高(51~75 Hz)等3段分别计算其反射能量并进行比较(图6),结果表明中低频情况下快变海底在中远偏移距下的反射能量均小于慢变海底情况,而在高频情况下两者相近。
此外,我们根据某地区实际海底起伏设计模型(图7a)并进行了数值模拟。该实际海底模型的均方根高为84 m,相关长度为5350 m。设水层速度为1500 m/s,下伏地层速度为3000 m/s,炮点位于水面中心位置,计算频率为0~40 Hz,主频为15 Hz。对此海底实际模型进行地震模拟,可计算得到其对应的反射能量曲线(图7b)及其透射能量曲线(图7c),可以看出,此实际模型的反射能量曲线变化与起伏海底界面复杂程度呈现出一定相关性,而其透射能量曲线与水平海底透射能量曲线相接近。

图6 不同频率下快变海底模型(a=22 m,细线)与慢变海底模型(a=220 m,粗线)的反射能量曲线

图7 实际起伏海底模型及其散射能量分析
3 结论与建议
(1)应用边界元法对复杂海底理论模型和实际模型的数值模拟与散射能量分析表明:快变化强起伏海底散射损失大,在进行海上勘探时建议变观以避开局部强变化海底的影响,或改变激发角度减弱散射损失。
(2)快变化海底散射引起地震波能量随偏移距起伏变化,变化规律与海底起伏具有一定相关性,据此可进行地表一致性校正。
(3)快变化强起伏海底,其散射能量在近偏移距变化很大且随偏移距衰减很快;起伏海底透散射作用弱于反散射作用。
(4)不同起伏海底对频率具有一定选择性,据此可在地震采集中针对实际海底调整激发频率以取得理想效果。
[1] HE Nanqun,MU Yongguang,LI Guibiao,et al.VSP migration using the boundary element method[C]∥Beijing(89)International Symposium on Exploration Geophysics.Beijing,1989.
[2] SÁNCHEZ-SESMA F J,CAMPILLO M.Diffraction of P,SV and Rayleigh waves by topographic features:a boundary integral formulation[J].Bull.Seism.Soc.Am.,1991,81:2234-2253.
[3] 徐世浙,王庆乙,王军.用边界单元法模拟二维地形对大地电磁场的影响[J].地球物理学报,1992,35(3):380-388.
[4] 徐世浙,阮百尧,周辉,等.大地电磁场三维地形影响的数值模拟[J].中国科学:D辑,1997,27(1):15-20.
[5] 符力耘,牟永光.弹性波边界元法正演模拟[J].地球物理学报,1994,37(4):521-529.
[6] FU L Y,WU R S.A hybrid BE-GS method for modeling regional wave propagation[J].Pure and Applied Geophysics,2001,158:1251-1277.
[7] SCHUSTER G T.The application of boundary integral equations to interactive modeling[C]∥The 3rd MIDAS Meeting.New York,1982.
[8] KAWASE H.Time-domain response of a semi-circular canyon for incident SV,P,and Rayleigh waves calculated by the discrete wave number boundary element method[J].Bull.Seism.Soc.Am.,1988,78:1415-1437.
[9] BOUCHON M,CAMPILLO M,GAFFET S.A boundary integral equation-discrete wavenumber representation method to study wave propagation in multilayered media having irregular interfaces[J].Geophysics,1989,54:1134-1140.
[10] FU L Y.Seismogram synthesis for piecewise heterogeneous media[J].Geophys.J.int.,2002,150:800-808.
[11] FU L Y.Numerical study of generalized lippmann-schwinger integral equation including surface topography[J].Geophysics,2003,68(2):665-671.
[12] FU L Y,WU R S.Infinite boundary element absorbing boundary for wave propagation simulations[J].Geophysics,2000,65(2):596-602.
Analysing seismic scattering characteristics of complex seabed by using the boundary-element simulation method
Li Xuxuan1Yu Gengxin2Fu Liyun2Wen Shuliang1Guan Xizhu2
(1.CNOOC Research Institute,Beijing,100027;2.Institute of Geology and Geophysics,Chinese Academy of Sciences,Beijing,100029)
The boundary-element method (BEM)has a good adaptability for simulating irregularly rough and complex seabed.The simulation accuracy of BEM for a complex fault model was compared with that of the finite-difference method,and the effectiveness of BEM was confirmed.BEM can be used to conduct wave simulation of rough seabed models,reflecting the impacts of rough seabed on seismic wave propagation.The statistical parameters were used to describe complex seabed topography,and then four types of rough seabed interface can be identified,i.e.fast lateral change,slow lateral change,strong vertical relief and weak vertical relief.The theoretical models of rough seabed can be build by selecting various statistical parameters,and BEM was used to make simulation of different theoretical models of rough seabed.Simultaneously,some actual seabed data was compared and the seismic scattering characteristics of complex seabed were analyzed.These results will provide some theoretical foundations for the seismic acquisition design of complex seabed and the optimization of seismic acquisition parameters.
the boundary-element method;complex seabed;seismic wave propagation;seismic scattering characteristics
*国家重点基础研究计划(973计划)项目“南海深水区复杂地质结构地震采集基础理论研究(2009CB219403)”资助部分研究成果。
李绪宣,男,高级工程师,现任中海油研究总院地球物理总师。地址:北京市东城区东直门外小街6号海油大厦(邮编:100027)。E-mail:lixx@cnooc.com.cn。
2010-10-26改回日期:2011-06-12
(编辑:周雯雯)

