阴阳直径等分圆的和谐美

廖红菊，邱云华

（恩施职业技术学院，湖北 恩施 445000）

阴阳直径等分圆的和谐美

廖红菊，邱云华

（恩施职业技术学院，湖北 恩施 445000）

用阴阳直径等分圆得到的圆形图案，有简单、对称、和谐之美。

太极图；阴阳直径；等分圆；和谐美

圆，一向被人们认为是最圆满、最完美的象征。很多数学爱好者研究过如何将圆n等分，多数是用（n为偶数）条直径或 n条（n为奇数）半径，借助量角器、圆规、直尺，便可快捷而有效地将圆n等分。如果我们用阴阳直径来代替传统的直径，或者用半圆代替半径，同样可以把圆n等分，创造的圆形图案更为和谐与协调。本文用阴阳直径等分圆，可以从中领略到圆的简单、丰富、对称、和谐之美。

1 太极图

设⊙O的直径为2r，将其任一条直径二等分，分别在此条直径的两侧以 r为直径作两个半圆弧，两个半圆弧构成的曲线将⊙O划分成了两个区域，一部分涂为黑色，另一部分为白色，便构成图1，称此图为“太极图”。其中黑白两部分是以圆心为对称中心的对称图形，每个区域的边界周长都等于⊙O的周长。它是以黑白两条鱼形纹组成的圆形图案，也称之为“阴阳鱼”。

太极图是图式最简单、内涵最丰富、造型最完美的图案，常常被人们用作装饰图案。

图1

图2

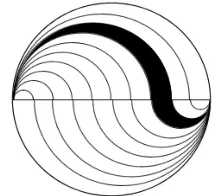
图3

图4

2 阴阳直径

太极图中两个半圆弧吻接而成的“S”分隔曲线叫“阴阳直径”。若将⊙O的直径等分为三段，在此直径的两侧分别以,为直径作半圆弧，四个半圆弧吻接而成的两条分隔曲线也叫“阴阳直径”，它仍将⊙O等分为三个区域，其中靠圆周边缘的两个区域是以圆心为对称中心的对称区域，中间区域是自身关于圆心对称的对称区域，如图 2，而且每个区域的边界周长都等于⊙O的周长。

事实上，中间区域的面积为

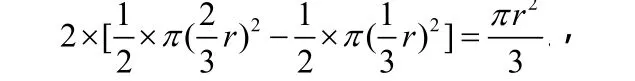
3 阴阳直径n等分圆

3.1 等分法一

设⊙O的直径为2r，将其任一条直径n等分，在此直径的同一侧分别以，，……，为直径作n－1个半圆弧，在引走的另一侧依照顺序，分别以，，……， 为直径作n－1个半圆弧，这2n－2个半圆弧成对吻接成n－1条阴阳直径，将⊙O分成n个相等的区域（如图3），且与首尾等距离的两个区域关于圆心对称，每个区域的边界周长仍等于⊙O的周长。

事实上，在图3中，第i个区域的面积为

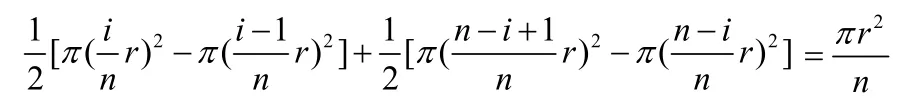
3.2 等分法二

设⊙O的直径为 2r，借助量角器、圆规将其半圆弧 n－1等分，得到 P1，P2，……，Pn共 n 个等分点，分别过点 P1，P2，……，Pn－1作直径，得到 2n－2条半径，在这 2n－2条半径的同一侧以r为直径作半圆弧，2n－2条半圆弧成对吻接成了n－1条阴阳直径。同样，这n－1条阴阳直径将⊙O等分为n个相等的区域（如图4），且每个区域是关于圆心对称的对称图形，每个区域的边界周长仍等于⊙O的周长。

由此可见，阴阳直径不仅可n等分圆，而且划分后，创造了一种更有意义的和谐美。

1 李 雍等著.数学和谐美［M］.大连：大连理工大学出版社，2009

2 张景中主编、易南轩著.数学美拾趣［M］.北京：科学出版社，2004

3 许 康、周复兴著.数学与美［M］.成都：四川教育出版社，1991

Harmony Beauty of Yin and Yang Diameter Equal Circle

Liao Hongju，Qiu Yunhua

The circular pattern, using yin and yang circle diameter to get equal circle, has a simple, symmetrical, and harmonious beauty.

Diagram; yin and yang diameter; equal circle; harmonious beauty

G642

A

1000－8136（2011）03－0148－01