关于分光光度法的新发现

袁秉鉴

(国营5409厂，山西省绛县 043606)

长期以来，人们一直认为：(1)光度法是基于化学物质对单一波长光的选择吸收；(2)光度法的理论基础是朗伯-比耳定律A=εbc，只因入射光波长和溶液吸收的非单一性，才造成了光度法的实际与定律的偏离；(3)用A=εbc的微分法可估量光度法测量的相对误差Δc/c，A在0.15～1.0时，Δc/c最小，在1%～2%之间[1-4]。笔者最近却有了新的发现[5,6]，现以高锰酸光度法为例进行详细介绍。

1 实验部分

1.1 主要仪器与试剂

分光光度计：727型，无锡市高速分析仪器有限公司；

硝酸溶液：1+3(约4 mol/L)、1+15(约1 mol/L)；

过硫酸铵水溶液：10%，现用现配；

Mn2+标准溶液：Mn2+浓度为1 mg/mL，硝酸浓度约1 mol/L，以金属锰、硝酸溶液(1+3)制备；

实验所用试剂均为分析纯；

实验用水均为蒸馏水。

1.2 实验方法

2 结果与讨论

图的吸收光谱

同法制备Mn2+显色溶液(0.5～65.0 μg/mL)15份，用1 cm比色皿，绘制520、530、560、580 nm的A-c曲线,如图2所示。

图吸收光谱带不同波长的A-c曲线

2.2 化学物质的的吸光规律

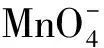
(1)

2.3 比色体系的消光规律

图2中各A-c曲线都有直线区间Lλ，表明比色体系(bc)(b为体系厚度，c为体系中吸光物质的浓度)对于它吸收谱带的任一波长λ，都有一个相应的吸收最灵敏的直线区间，这是光度法定量测定可靠性的基础。但它们并不符合A=εbc，所以应重新讨论它们间的关系。

当吸收谱带中强度为I的光透过比色体系(bc)时，其强度I的衰减-dI应与光强I、体系(bc)中吸光物质基态与光截面上光子的碰撞概率P、比色体系的吸光层d(bc)成正比，即：

-dI=K1IPd(bc)

(2)

碰撞概率P是由吸光物质浓度和光强I两个因素决定的，但图2的直线区间Lλ表明，在这一区间它的量值最大(等于1)，则式 (2)可转化为：

-dI/I=K2d(bc)

(3)

将该式在Lλ区间内积分，并根据吸光度A的定义，整理后得到：

ΔAP=KΔ(bc)P

(4)

注脚P表示式(4)仅限于Lλ区间。式(4)表明：对于吸收谱带内的任一波长，比色体系必然有一个与它相应的“吸收”(实际不全是吸收，包含一定的散射和反射，下同)最灵敏区间Lλ(会因仪器不同而不同)。在此区间内，体系对波长λ的吸光度改变量ΔAP与体系的改变量Δ(bc)P成正比；体系厚度b恒定时，吸光度改变量ΔAP与体系内消光物质浓度的改变量ΔcP成正比：

ΔAP=KΔcP

(5)

称这一规律为“比色体系的消光规律”，简称“消光规律”。试样含量cX可由两个合适的标准样品(c1、c2)确定，既不能用A=εbc换算，也不必用“多标准回归”，而可用“两标法”计算，公式如下：

cX=(c2-c1)(AX-A1)/(A2-A1)+c1

(6)

A1、A2和AX，分别为标准样品(c1、c2)及试样(cX)的吸光度。

公式(4)的推导过程表明，A-c曲线两端所以偏离直线，是因为消光粒子与光截面上的光子碰撞概率P在Lλ区间以外，因消光物质浓度c和光强I的变化而不断变小的结果。

2.4 光度法的测量误差和“精密度法则”

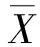
Di=0.7R

(7)

图3 大样本正态分布

图4 小样本及其均值分布

2.5 “精密度法则”是正态分布理论在测量中的具体体现

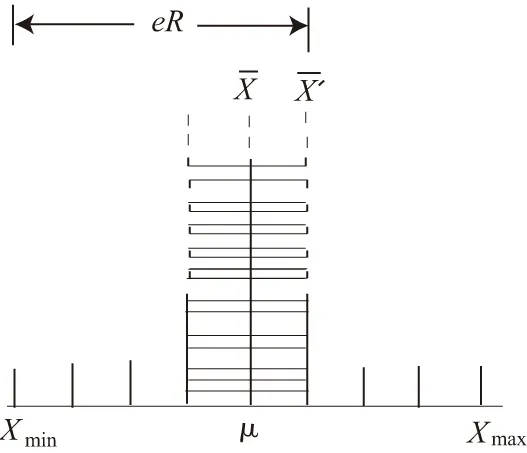
图5 小样本及其均值分布

因为“小样本”与JJF 1059-1999规范4.1的重复性测量相同[11]，所以其均值的标准不确定度为：

(8)

(9)

(10)

因为“小样本”近似正态分布[13]，s可用极差法求得[14]。根据对大量n=4～12的“小样本”s的数据观察，取n=8，s=0.35R，代入式(9)和 式(10)得：

(11)

(12)

上面公式表明，遵循“精密度法则”的“小样本”的不确定度与样本极差成正比，与样本容量的平方根成反比。实践证明，只要极差可确定，它们对n=4～12的“小样本”都是适用的。

3 应用检验

表光度法对标准样品的测定结果 %

4 结论

“比色体系的消光规律”表明，光度法的入射光可以是非单一波长的光带，比色体系可以是非纯吸收的均匀体系。光度法是分析化学的一个不可缺失的分支，它有5大特点：(1)应用范围广，无机、有机、元素、分子的都可用该法测定；(2)测定的含量范围宽，可从0.00%直到100%；(3)标准样品容易配制；(4)干扰因素容易消除；(5)容易实现多组分的联测[15]。

[1] 罗庆尧，邓延倬，蔡汝秀，等.分光光度分析[M].北京：科学出版社，1998：57-370.

[2] 董元彦，张方钰，王运，等.无机及分析化学[M].北京：科学出版社，2006：313-327.

[3] [美]查尔斯·K·曼，托马斯·J·韦克斯，威尔逊·M·古里克.仪器分析[M].冉顺善，潘德慧，成荣钊，等译.北京：化学工业出版社，1983：426-448.

[4] [美]加里·D·克里斯琴.分析化学[M].3版.王令今，张振宇译.北京：化学工业出版社，1988：430-470.

[5] 袁秉鉴. 高锰酸分光光度法的研究[J]. 化学分析计量，2006,15(2)：13-17.

[6] 袁秉鉴. 光度法应用探讨[J]. 化学分析计量，2008,17(3)：35-38.

[7] 吴诚.机械工程材料测试手册[M].沈阳：辽宁科学技术出版社，1996：1 047-1 065.

[8] GB/T 4883-2008 数据的统计处理和解释 正态样本离群值的判断和处理[S].

[9] 吴梅村.数理统计学基本原理和方法[M].成都：西南财经大学出版社，2006：112-163.

[10] 黄坚，刘德光.概率论与数理统计[M].北京：科学出版社，2010：93.

[11] JJF 1059-1999 测量不确定度评定与表示[S].

[12] 郑德如.统计学[M].上海：立信会计出版社，1994：173-174.

[13] 刘智敏.误差与数据处理[M].北京：原子能出版社，1981：14-64.

[14] 李慎安.测量不确定度百问[M].北京：中国计量出版社，2009：59.

[15] 袁秉鉴.光度法快速测定不锈钢中的铬、镍、钼、钛、锰[J]. 化学分析计量，2010,19(1)：55-57.