柔性接触网吊弦长度精确计算

赵红玉,梅桂明,范海江

(1.铁道第三勘察设计院集团有限公司,天津 300251；2.西南交通大学牵引动力国家重点实验室，成都 610031)

1 概述

为了改善接触网一跨内弹性不均匀,接触网一般采用弹性链型或复链型结构形式,同时兼顾到施工难度、维护时间等因素,临近下锚端的几跨采用简单链型,中间跨采用弹性链型。众所周知,接触网的施工质量直接影响着受电弓-接触网系统的受流质量,而接触线又是通过吊弦悬挂在承力索上,它的高度变化完全由吊弦长度来控制,这说明吊弦长度的预配是非常重要的。文献[1～6],从经典力学或有限元角度提出吊弦长度的计算方法,得出较为满意结果,其中文献[1,3～6]对简单链型悬挂接触网吊弦长度进行了分析研究,文献[2]从经典力学角度推导出弹性链型悬挂接触网吊弦长度计算,但是模型只是在简链或弹链单一状态下,主要对单跨接触网进行受力分析,与实际情况有所出入,基于此,本文对简单链型、弹性链型混合状态下,采用迭代算法进行吊弦长度的精确计算。

2 数学模型

柔性接触网由接触线、承力索、辅助承力索、吊弦及其线夹等组成,具有一定的抗弯特性,将其处理为欧拉梁单元,并考虑到在预张力作用下几何刚度影响,其弹性刚度矩阵、几何刚度矩阵及刚度矩阵分别为[7～8]

(1)

(2)

[K]=[Kl]+[Sl]

(3)

式中,L为单元长度；EA为抗拉刚度；EI为抗弯刚度；F为张力。

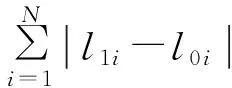
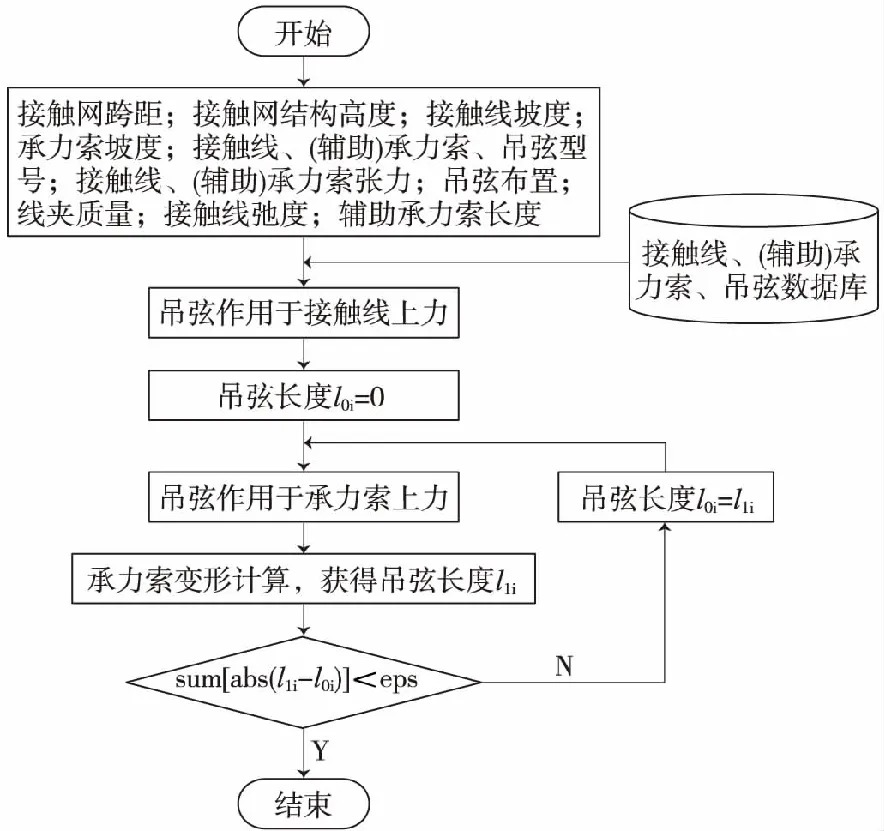
图1 吊弦长度计算流程

3 算例

取20跨简单链型、弹性链型悬挂混合配置的接触网,其跨距为50 m,结构高度1.6 m,接触线线材及张力分别为CTMH150、30 kN,承力索型号及张力分别为JTM120、21 kN,辅助承力索型号、张力及长度分别为JTMH35、3 500 N、18 m,其几何、力学性能参数见文献[9，10],吊弦型号为JTMH10,一跨内吊弦布置为5、13、21、29、37、45 m,线夹质量为0.2 kg,接触网为5跨锚段关节,中心柱、转换柱、下锚柱处为简单链型,其他为弹性链型,离下锚柱远的转换柱处接触线抬高150 mm,离下锚柱近的转换柱及下锚柱处接触线抬高500 mm。

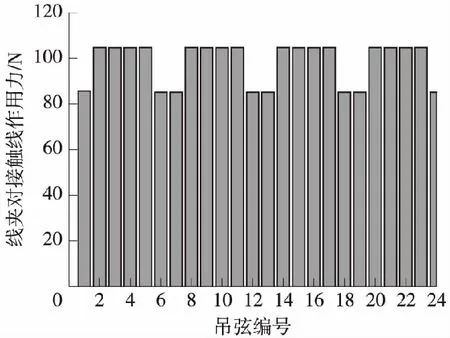
图2 前4跨线夹对接触线作用力

根据本文提出的计算方法,计算出线夹对接触线作用力,如图2所示。其值基本上以跨为呈周期性变化,临近支柱两侧的吊弦作用力小,中间吊弦作用力大,在此状态下,与接触线连接的吊弦下端处于同一高度,接触线张力不会造成相邻吊弦处对接触线的作用力差异,其值基本上为接触线重量分配值。然而临近下锚端接触网结构形式变化,结构为简单链型,在定位点处没有安装辅助承力索,在其他布置不变情况下,作用于承力索上力减小,承力索变形也相应减小,导致吊弦长度大于相应弹性链型状态,如图3所示。进一步了解简单链型、弹性链型结构对吊弦长度影响,计算出承力索最终状态,如图4(a)所示,对于中间跨的弹性链型接触网,辅助承力索的最终状态以该处支柱呈对称形式,而对于弹性链型与简单链型交界处接触网,辅助承力索的最终状态则不为对称形式,如图4(b)所示。根据该组吊弦长度,建立接触网系统的有限元模型并进行计算,其变形前、后结果如图5(a)所示,几乎重合,在此状态下,吊弦处接触线位移如图5(b)所示,与理论值偏差最大值为1.26 mm,完全符合铁路接触网施工要求。

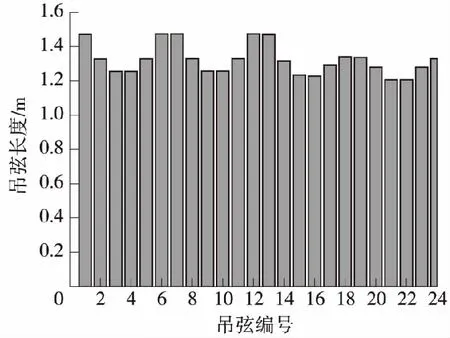
图3 前4跨吊弦长度

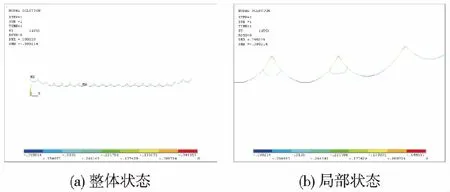
图4 承力索最终状态

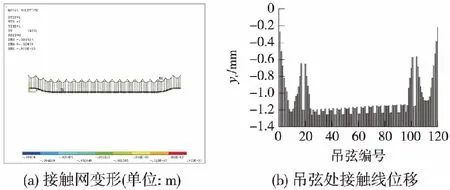
图5 接触网变形及吊弦处接触线位移

4 结论

接触网在电气化铁路尤其是高速客运专线的建设中起着重要作用,长期的实践与研究表明,接触网与受电弓之间实现电能稳定、有效地传输,是实现列车运行速度目标值的关键因素。为提高接触网施工质量,改善弓网受流质量,一般现场都会有严格的腕臂、吊弦预配计算。经与实践计算值比较,本文所提出的简单可行的迭代算法来求解柔性接触网吊弦长度,有效地减小了吊弦预配长度的计算误差,其计算结果能够使得接触线处于理想状态,最大偏差1.26 mm,完全符合铁路接触网施工要求。

[1] 昌月朝.简单链型悬挂吊弦长度计算方法[J].铁道机车车辆,1998(2):30-34.

[2] 昌月朝.弹性链型悬挂吊弦长度计算方法[J].铁道机车车辆,1998(4):41-48.

[3] 李刚,梅桂明.简单链型悬挂接触网静态形态计算新方法[J].电气化铁道,2011(1).

[4] 李瑞平,周宁,梅桂明,张卫华.初始平衡状态的接触网有限元模型[J].西南交通大学学报,2009(5).

[5] 周 宁,李瑞平,张卫华.基于负弛度法的接触网建模与仿真[J].交通运输工程学报,2009(4).

[6] Mei G M, Zhang W H, Zhao H. Y., Zhang L. M. A hybrid method to simulate the interaction of pantograph and catenary on overlap span[J]. Vehicle System Dynamics, 2006,44(Suppl):571-580.

[7] 付秀通.轮/轨—弓/网系统耦合动力学数值模拟分析与试验研究[D].北京：中国铁道科学研究院,1996.

[8] 梅桂明.受电弓/接触网垂向耦合动力学研究[D].成都：西南交通大学,2001.

[9] 中华人民共和国铁道部.TB/T 2809—2005 电气化铁道用铜及铜合金接触线[S].北京：中国铁道出版社，2005.

[10] 中华人民共和国铁道部.TB/T 3111—2005 电气化铁道用铜及铜合金绞线[S].北京：中国铁道出版社，2005.

[11] 朱飞雄.接触网弹性链形悬挂的设计、施工与检测要点[J].铁道标准设计，2008(1).