软岩交叉巷道开挖围岩稳定性数值模拟分析

李龙福,金爱兵,邓富根,刘 波

(北京科技大学土木与环境工程学院，北京 100083)

软岩问题一直是世界性难题，特别是随着开采深度的增加，软岩问题如两帮鼓胀挤出、顶沉底鼓、巷道全断面收缩等越来越严重，直接影响到矿山安全生产，危及井下作业人员的人身安全。因此，确定合理的支护方案，显得尤为重要。但要想有效的进行软岩巷道的支护，必须根据软岩巷道所处的工程地质环境，进行围岩稳定性分析，选择合理的支护参数，确定最佳支护时间和最佳支护时段[1-3]。

北洺河铁矿位于武安断陷盆地西缘，在NNE向的玉泉岭-矿山村-茶村断裂带的西侧，区内为次一级的NWW向的褶曲构造所控制，以褶皱为主，断裂次之，属接触交代“矽卡岩型”铁矿床，矿体埋深为136～679m，采用无底柱分段崩落法开采。自开采以来，该矿就对软岩巷道的支护问题进行了研究，但是在巷道使用过程中，出现了越来越多的地质灾害，如巷道底鼓、片帮、冒顶等，尤其是在联巷与进路的连接处，围岩暴露面积大、受力状态差，是采场中最容易变形破坏的区段，严重影响了矿山正常生产的需要。

针对上述实际情况，在相关研究的基础上[4-8]，以北洺河铁矿300m采深的采准切割工作中出现的交叉巷道为研究对象，结合现场勘察、室内数值模拟研究、巷道收敛监测反分析等手段，研究交叉巷道在开挖过程中围岩的应力、位移、塑性区分布特征及规律，为施工设计提供有效的参考依据。

1 模型的建立

模型采用十字型交叉巷道，位于模型中部，分别为巷道a和b，巷道断面为半圆拱直墙形，宽4m，墙高2m，拱半径2m，巷道埋深300m。根据圣维南原理及实际经验，局部开挖仅对距离巷道3～5倍跨度范围内有影响。因此，模型尺寸为：长×宽×高=30m×30m×27m，共计单元总数为26×112，网格节点总计28×490个，开挖部分以空模型模拟(Null Model)。模型采用位移边界条件：四周采用滚支撑(ux=0,uy=0)，底部固定(ux=0，uy=0，uz=0)，上部边界为上覆岩体的自重应力，σzz=-7.9MPa，岩体的水平应力σxx=σyy=0.37σzz。计算时，采用Mohr-Coulomb应变软化准则[9-10]，计算采用的基本力学参数见表1。由于模型的对称性，a、b巷道的开挖顺序对计算结果不产生影响，将两条巷道的开挖分3步完成，见表2。

表1 岩体物理力学参数

表2 巷道开挖步数与开挖长度

2 模拟结果分析

2.1 完成第1步巷道a开挖

对巷道a进行开挖不支护模拟，以了解该巷道开挖后，围岩的二次应力分布情况。

开挖引起两帮垂直应力的增加和顶底板围岩垂直应力的降低。其中，顶底板垂直应力从-2MPa逐渐过渡到-8MPa(在FLAC3D中，负号表示压应力，正号表示拉应力，以下同)，两帮应力呈对称分布，其中在两帮中下部出现应力集中，达到-14.5MPa，并沿巷道径向逐步过渡到原岩应力状态。受开挖的影响，应力扰动区约在离帮壁5m范围之内。最大主应力σ1为-14.73MPa，出现在两帮靠中下部围岩中，顶底板的最大主应力σ1为-0.43MPa～-4MPa。巷道开挖造成围岩最小主应力σ3的降低，在巷道四周为-3.65MPa，并在巷道底部中央出现-0.87MPa的拉应力，须注视该处的支护。剪应力中最大正剪应力为4.094MPa，最大负剪应力为-4.095MPa，最大正负剪应力分别沿右拱角-左边墙角与左拱角-右边墙角分布，开挖后将造成两帮和墙角大面积的剪切破坏，交叉口顶底板的剪应力大小分别为2.0MPa、1.0MPa。在主要位移点中，拱顶垂直位移为-47.6mm，底板向上位移34.9mm，相对收敛值82.5mm，远超过《采矿设计手册》[11]规定的相对收敛值36mm的上限，应采取支护手段。由塑性区分布云图可知，两帮及墙角处主要受到剪切破坏，顶底板主要受到拉伸破坏，两帮出现2m范围塑性区，顶底板的塑性区为巷道周边1m以内，相比较而言，墙角和拱顶部位的塑性破坏较为严重。

2.2 第2步巷道b开挖至交叉口

在掌子面的端部围岩中出现应力集中，达到-15.7MPa。最大主应力σ1出现在交叉口顶板和底板部位，量值在-14MPa～-16MPa之间。由于巷道b的开挖，在交叉口部位使得受到应力扰动的范围扩大一倍左右，而且在巷道的四周普遍出现0.5MPa的拉应力，围岩的受力状态下降。顶板和底板的垂直位移值增大，分别达到-66.8mm和43.5mm。巷道a受到的正负剪应力分别为4.26MPa、-4.16MPa，剪应力略有增加，在交叉口拱顶与底板的剪应力分别为-3MPa、1.0MPa，与之前相比，顶板剪应力增加。根据塑性区分布云图，交叉口拱顶塑性状态有所改变，由受拉变为拉剪共同作用，受力状态恶化，为提高交叉口巷道的稳定性，应提高支护等级。

2.3 完成巷道b剩余部分的开挖

根据垂直应力云图，在巷道交叉口应力状态发生改变，由原先的应力集中变为应力降低区。最大主应力σ1出现在巷道的两帮，大小为-12MPa～-15MPa，应力集中程度和只开挖巷道a相比略有增加。拱顶处的最大主应力为-2MPa，与先前相似。在最小主应力σ3云图中，巷道底板和交叉口拱顶处，受到约0.8MPa的拉应力。在剪应力云图中，巷道a的剪应力进一步增加，最大正负剪应力分别为4.32MPa、-4.27MPa,交叉口拱顶和底板的剪应力分别为-1.0MPa、-2.0MPa，与上一步相比，顶板受剪情况得到改善，底板剪应力增加，这与塑性区分布云图中显示的结果相对应，表明由于巷道b的开挖使得巷道a的应力重新分布，其结果是交叉部分应力得到释放，巷道a、b两帮应力集中。在主要位移点中，交叉口拱顶部位的最终沉降量为88.5mm，交叉口底部的最终底鼓为53.3mm。

数值模拟结果表明，巷道a开挖完毕后，围岩在初始地应力场作用下，向开挖临空面方向移动，产生不均衡变形，改变了应力场的空间分布特征，在一些应力集中区域，会出现围岩的破坏现象；巷道b开挖后，围岩应力发生转移，总体上表现为应力从交叉口处向巷道a、b两帮转移，交叉口应力得到释放。

3 巷道围岩位移监测与分析

巷道开挖后，由于所处的应力状态发生改变，打破了开挖前的应力平衡状态，围岩会通过变形和应力的调整来达到一个新的平衡。因此，通过关键点位移的监测，对模拟结果与实测结果进行比较分析，一方面可以验证数值模拟的合理性，另一方面也可以定性地了解巷道在开挖后的变形趋势。图1与图2分别为巷道交叉口拱顶沉降监测曲线和模拟曲线。

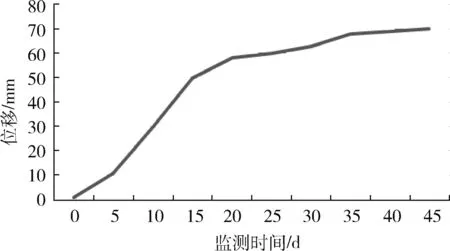
图1 巷道交叉口拱顶沉降监测曲线

图2 巷道交叉口拱顶模拟曲线

根据图1与图2可以得出以下结论：①埋深300m处的交叉巷道交叉部位拱顶沉降的模拟结果显示拱顶沉降最大位移为88mm，与实测最大位移71mm比较接近，从侧面反应了数值模拟计算对应力释放率把握较为接近实际情况；②巷道收敛变形的实际监测曲线与数值模拟曲线变形趋势一致，变形值也较为接近，由此说明数值模拟对巷道开挖后的二次应力分布模拟与实际情况较为接近，数值模拟结果可以进一步为巷道围岩稳定性评价和支护设计提供理论依据。

4 结论

采用无底柱分段崩落法开采，具有开采强度大、作业效率高、成本低和生产安全等优点，在金属矿山迅速得到推广，特别是在铁矿山更为广泛。但在采准切割工作中出现大量交叉巷道，且其应力应变分布复杂。本研究通过FLAC3D有限差分数值模拟计算方法，分析了交叉巷道在开挖前后，围岩应力、位移和破坏区分布及其变化规律。

1)开挖引起两帮垂直应力的增加和顶底板围岩垂直应力的降低，在帮壁中下部位出现应力集中；受开挖的影响，在巷道底板出现较大的拉应力，特别是在软岩工程中，尤其应当注意；在两帮及墙角处主要受到剪切破坏，顶板主要受到拉伸破坏；应力扰动范围约5m，两帮塑性区约2m,顶底板塑性区约1m。

2)巷道交岔点处应力随着开挖进程呈现增加趋势,尤其是当第二条巷道挖到交岔点时,应力的重新分布造成交叉处顶底板出现应力集中,且在帮壁四周普遍出现拉应力，围岩受力状态下降，扰动范围扩大。

3)由于巷道b剩下部分的开挖，应力向交叉口两边转移，结果是交叉口应力得到释放,巷道a、b两帮应力集中。

4)随着巷道开挖不断推进，巷道位移呈增加趋势，最大下沉位移和最大底鼓分别发生在交叉口处顶底板中央，在此处应增加支护等级，以维护巷道的稳定并进行实时监测。

5)巷道收敛变形的数值模拟结果和实际监测结果对比分析说明，数值模拟只是一种工程模拟方法，要真正达到设计的信息化和最优，必须辅以现场监控量测来获得实际施工程中的围岩力学动态，以调整工程类比法的设计参数和数值模拟的参数取值，才能客观地反映出地下工程在施工过程中，围岩应力、位移及塑性区分布等特征。

[1] 何满潮,景海河,孙晓明.软岩工程力学[M].北京:科学出版社, 2002.

[2] Zhao Xufeng,Wang Chunmiao, Kong Xiangli. Analysis of time-space effects of construction behavior of deep soft rock tunnel[J]. Chinese Journal of Rock Mechanics and Engineering,2007,26(2):404-409.

[3] Liu Zhichun, Li Wenjiang, Zhu Yongquan, Sun Minglei. Research on construction time of secondary lining in soft rock of large-deformation tunnel[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(3):580-588.

[4] Karman Fifer BizTalk*, Borut Petkovek. Displacement analysis of tunnel support in soft rock around a shallow highway tunnel at Golovec[J]. Engineering Geology,2004,75(1):89-106.

[5] Yang Zhifa, Wang Zhiyin, Zhang Luqing, et al. Back-analysis of viscoelastic displacements in a soft rock road tunnel[J]. International Journal of Rock Mechanics & Mining Sciences,2001,38(3),331-341.

[6] 周传波,郭廖武,姚颖康,等.采矿巷道围岩变形机制数值模拟研究[J].岩土力学,2009,30(3):655-656.

[7] 杨超,崔新明,徐水平.软岩应变软化数值模型的建立与研究[J].岩土力学，2002,23(6):695-697.

[8] 匡忠祥,宋卫东,邓成爱.采准巷道交岔点围岩受力状态的三维数值模拟研究[J].金属矿山,2007,375(9):46-49.

[9] 彭文斌.FLAC 3D实用教程[M].北京:机械工业出版社，2007.

[10] 陈育明，徐鼎平.FLAC/FLAC3D基础与工程实例[M].北京:中国水利水电出版社，2008.

[11] 采矿设计手册编辑委员会. 采矿设计手册:井巷工程卷[M].北京:中国建筑工业出版社,1989.