基于计盒法的棉绉织物灰度曲面分形特征的研究
赵维强,杨 艳(, )
1 前言
棉绉织物具有凹凸不平、粗糙、不规则的表面纹理[1],其起绉程度有大有小、绉纹分布有粗糙有细密,这些不同的形态直接影响到织物的视觉效果和其它风格。绉效应,是指绉纹特征在人脑中的映象,关于绉效应的形成机理,许多行家们都已进行了卓有成效的研究,而对于绉效应的评定,并没有一个统一的标准,人们往往把织物与自己心目中的“标准”进行比较,这种方法属于主观评定,受主观因素影响较大,很难得到一个统一的、精确的结果。
计算机图像处理技术是近几年应用于纺织业的一种新兴的处理手段。随着计算机速度的提高以及内存的增加,计算机图像处理的手段与方法更为广泛。计算机图像处理技术可以直观地对图像进行变换,提取特征信息,因此用于分析评定绉织物的起绉程度有很大的优势。美国有一些学者探讨了利用计算机图像处理技术评定织物的折皱程度。我国学者也已探讨了利用数学形态学方法和频谱分析法评定双绉织物的起绉程度[2-3],提出以起绉度、云斑重复率、云斑形状复杂度、频谱图来评价绉织物的起绉状况。
本文采用的图像为灰度图像。对于灰度图像而言,把二维图像视作一个三维空间中的一个表面(x,y,f(x,y)),其中f(x,y)为图像(x,y)位置处的灰度值,即亮度值,于是图像灰度的变化情况将反映在该表面的粗糙程度上。理想条件下如果棉绉织物是绝对平整的,那么每一点的灰度值应该相等,因此,在以灰度为纵坐标z、以位置为平面坐标xy的系统中,该图像灰度曲面为一平整平面;随着织物绉效应的增加,该灰度曲面的起伏将会加剧。棉绉织物表面的灰度曲面具有明显的自相似性,符合分形理论分析的条件。因此 ,本文利用分形理论对棉绉织物表面图像的灰度曲面进行了分形特征的分析 ,并用计盒法计算其分形维数,以评定棉绉织物的绉效应。
2 实验
2.1 实验材料
选取不同起绉程度的五块棉绉织物为研究对象,其中1号试样起绉程度最重,起绉等级设为1级;5号试样起绉程度最轻,起绉等级设为5级;试样2、3、4号起绉等级分别为2级、3级和4级。
2.2 图像的获取与预处理
利用计算机图像输入系统,首先将样品放置于低倍显微镜下,在反射光照射下,通过CCD摄像头将织物图像输入到计算机中,图像为256×256像素,相当于实际尺寸为0.85 cm×0.85 cm。
棉绉织物图像在输入计算机过程中,由于受到光照不匀和显微镜视场的影响,所得图像有明显的中间亮、四周暗以及靠近光源一侧亮、而远离光源一侧暗的现象。为了消除这一影响对织物图像进行预处理,它主要包括消除背景、对比度增强、中值滤波去噪等预处理。预处理后的图像如图1所示。

图1 棉绉织物预处理后的图像
3 结果分析
分形的一个重要特征就是无标度性,即在不同尺度上表现出相同的粗糙性和破碎性。自然界中的分形往往具有一个最小标度和最大标度,即无标度区间。只有在无标度区间,才存在分形规律[4-8]。本文对无标度区间的确定是,首先作出lnN(λ)与lnλ的曲线图,找出线性关系好的一段,作为无标度区。并用最小二乘法作一元线性回归拟和出直线的斜率,作为分形维数的估计值。
表征灰度分布的分形维数可以用来反映灰度的起伏程度。维数越大,则灰度起伏程度也越大。由计盒法得到的lnN(λ)与lnλ的关系图如图2所示。由图2可以看出,曲线的中间段呈良好的线性关系,可以用于计算分形维数D。计算结果如表1所示。
由表1中的R2可知,lnN(λ)与lnλ具有非常好的线性关系,说明棉绉织物表面图像的灰度分布具有显著的分形特征。起绉程度最严重、起绉等级为1级的试样1,分形维数最大为2.814;起绉程度最轻、起绉等级为5级试样5,分形维数是2.337;其它试样的起绉等级分别为2级、3级、4级,分形维数分别为2.665、2.578、2.494,分形维数的差异较明显,可以用来评价棉绉织物的起绉程度。

图2 存在无标度区间的关系曲线
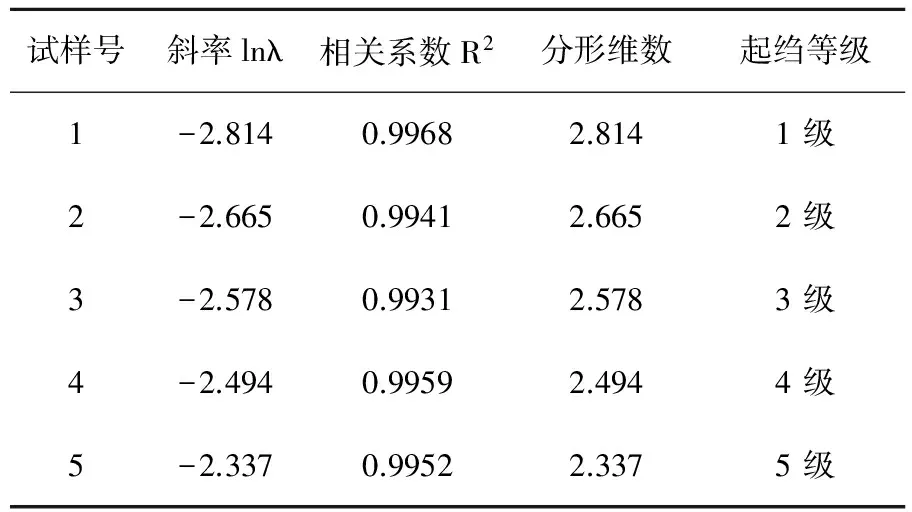
表1 计盒法计算灰度曲面起伏的分形维数
本文的图像处理过程和计盒法记数过程均用MATLAB和VC++语言编程进行。
4 结论
本文利用分形理论分析了棉绉织物的绉效应,得出一些结论:
(1)棉绉织物表面的灰度分布存在显著的分形特征;维数可以通过计盒法计算求得。
(2)棉绉织物灰度曲面的起绉维数与织物表面的视觉风格有关,起绉程度相似的织物其维数接近;起绉程度大的织物其维数也大;纹理粗糙的起绉维数与纹理细密的起绉维数存在明显的差异,故可以用灰度曲面的分形维数来评价绉织物的起绉程度。
[1] 蔡陛霞.织物结构与设计[M].上海:中国纺织出版社,2004.
[2] 王正知,李栋高.双绉绉效应的计算机视觉评价——数学形态学方法[J].苏州丝绸工学院学报,1994,14(4):110—117.
[3] 王正知,双绉绉效应的计算机视觉评价——频谱分析法[J],苏州丝绸工学院学报,1994,14(4):118—126.
[4] 张济中.分形[M].北京:清华大学出版社,1995.
[5] 董莲科.分形理论及其应用[M].大连:辽宁科学技术出版社,1991.
[6] 辛厚文.分形理论与应用论文集[M].合肥:中国科学技术大学出版社,1993.
[7] CHAUDHARIB B,SARKAR N.Texture Segmentation Through Fractal Geometry[J] .IEEE Trans on PAMI,1995,17(1):23—35.
[8] 李后强等.分形理论及其在分析科学中的应用[M].北京:科学出版社,1997.

