考虑大规模光伏电源接入系统的发电机组检修计划

张 俊

(恩施州电力总公司，湖北 恩施 445000)

随着以石油为代表的化石能源资源的减少和燃用化石能源对气候和生态环境的破坏，能源问题日益成为制约社会发展的瓶颈.为了摆脱能源危机，开发清洁可再生能源已经成为世界各国经济和社会可持续发展的重要战略.太阳能光伏发电以其储量丰富、分布广泛和无污染等优势而备受关注[1-3].光伏发电技术作为可再生能源利用的重要组成部分，得到了众多国家政府的大力扶持，并相继出台有关政策，加大光伏发电产业的发展力度，使得光伏发电建设已进入了一个快速发展的时期.

大型集中式并网光伏电站是一种重要的光伏发电形式.大型集中式并网光伏电站并入电网将对系统电压分布、功率传输、网络损耗等稳态性能带来不可忽视的影响.为了保证电力系统的安全运行，发电机组都应有计划地进行周期地的预防性检修，使设备能经常保持良好的技术状态，以减少故障、延长寿命.当发电机组停下检修时，备用容量减少，系统的可靠性将会降低，因此，合理安排机组的检修计划，使系统可靠性下降不至过多，或增加检修备用容量最少[4-6].

综合考虑大规模光伏发电功率波动特性、发电机组的检修特性与调峰能力，以最小的检修成本与弃光伏发电量安排发电机组检修计划，为短期发电计划预留足够的调峰能力，从而保证电网的安全可靠运行.

1 数学模型

1.1 系统结构

常规发电机组可分为日内不可多次启停机组与日内可多次启停机组.核电、大型火电以及热电为不可日内多次启停，可以用一个机组组合变量表示其每一日内开停状况.水电、抽水蓄能、燃机可日内多次启停.为了对每日内所有的机组类型都可用一个统一的机组组合变量表示，可以认为机组在日内始终开机，当出力为0时,代表了其实际处于停机状态.

为简化模型，优化计算每个检修计划决策时段的最小弃光伏发电量，本文将低谷时段的弃光伏发电量近似为检修计划决策下的电网的弃光伏发电量，且不考虑输电网络约束.

1.2 目标函数

发电机组检修计划的安排实质上是一个多目标、多约束的优化问题.考虑到光伏发电的特点，在此以检修费用最小、系统低谷负荷时弃光伏电量最小为目标函数.

1)检修费用最小

(1)

式中：Cit表示机组i第t时段的检修费用；Xit表示机组i第t时段的检修状态，Xit=0表示机组检修，Xit=1表示机组未检修.

2)系统低谷负荷时弃光伏系统电量最小

在临界情况下，任意时刻，系统中有功功率平衡，此时有:

(2)

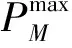
当系统备用不足且光伏系统大发时，将出现大量的低谷弃光伏电量，此时有:

(3)

式中：t检修周期内某一时段的时段标号；T为检修周期内的时段总数；f(ξ)为光伏系统输出功率的概率密度函数.

式(3)是在检修计划决策周期T内对光伏系统各时段弃电量数学期望值的求和.

3)多目标优化的妥协模型目标函数

对发电机组检修计划优化问题的多目标通过加权求和，可以建立多目标优化的妥协模型，目标函数数学公式可以表示如下：

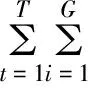
(4)

式中，k1、k2表示各个目标的权重.

1.3 光伏发电概率函数

由于光照强度具有随机性，因此光伏发电系统的输出功率也是随机的.据统计，在一定时间段，光照强度可以近似看成Beta分布[7-9]，其概率密度函数如下：

(5)

式中：α、β为Beta分布的形状参数；r和rmax(W/m2)分别为该时段内的实际光强和最大光强.

假设给定一个具有M个电池组件的太阳能电池板，其总的输出功率为：

PM=rAη

(6)

式中，A为太阳能电池板的总面积，η为太阳能电池板的光电转换效率，它们分别为：

(7)

(8)

式中，Am(m=1,2,…,M)为每个组件的面积，ηm(m=1,2,…,M)为每个组件的的光电转换效率，已知光照强度的概率密度函数，通过式(5)可以得到太阳能电池板输出功率的概率函数也呈Beta分布，即:

(9)

式中：RM=Aηrmax为方阵最大输出功率.

1.4 约束条件

为保证系统的安全可靠运行，合理有序开展检修工作，应考虑检修计划优化问题包括的大量约束条件.根据约束源的不同，检修计划的约束源一般可分为三种类型[10-12]：

第一类由发电机检修技术所确定的约束.包括机组检修开始时段要求、检修持续时间的允许范围、机组检修连续性要求、机组检修时序要求、机组检修间隔要求等约束条件.

第二类由可用人力及材料资源限制而确定的约束.由于检修人员数量及技术能力、设备能力限制，使得能同时进行检修的设备数量有限.

第三类由电力系统运行特点所要求的约束.包括电网潮流与稳定性要求、系统可靠性的要求、季节性或其他原因的禁止检修约束等.

在上述各种约束中，有些约束是必须满足的严格约束，有些约束则有一定的松弛度.考虑到含光伏发电系统的接入，发电机组检修的约束条件为：

1)检修规程约束

(10)

式中：tmin,tmax分别为机组i的最早和最迟申报检修时间.

2)机组检修连续性约束

(11)

式中：t为机组i检修的时段；Δti为机组i检修持续周期.

3)电网正负备用容量约束

(12)

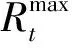
2 模型的求解与仿真

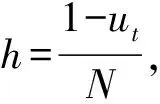
(13)

于是，目标函数转换为:

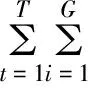
minF=k1Cit(1-Xit)+k2ft(1)+k2(ξk-γt)ft(ξ)] (14)

3 算例分析

为了保证算例中最为关键的光伏发电Beta参数选取的真实性与科学性，利用HOMER软件根据事先指定地点每个月份的光强值计算出的光照强度平均值μ和方差σ[14]，可以得到光强Beta分布参数，具体计算公式如下[15]：

(15)

(16)

由此可以得到式(9)所示光伏发电有功出力的随机分布.由Beta分布的定义可求出各阶矩，其k阶矩如下：

(17)

本文的算例用12时段表示，假定光伏发电系统的总装机容量设为8 MW，12时段的峰谷负荷曲线的平均峰谷差率为40%，负荷曲线具有典型春季负荷的特征.除光伏发电外，系统共有8台发电机组，全部申报检修计划，机组参数如表1所示.全系统总装机容量为100 MW，其中光伏发电装机容量占8%，无调峰能力机组装机容量占20%.

设定k1=1，k2=10.在该参数下，系统以尽可能满足光伏上网需求、减少低谷时段弃光伏发电量为优化目标，在此目标满足的情况下，再根据各机组检修成本的高低，安排决策检修计划.并设定目标函数积分项分段线性化的分段值N=5.检修计划优化决策结果如表2所示.为了保证系统在各检修时段有足够的调峰能力，调峰能力较强的机组如机组1(抽水蓄能)与调峰能力较弱的机组如机组3(热电)一起安排检修，从而验证了本文模型对系统调峰资源的合理优化配置能力.

表2 调整的机组检修计划

4 结论

大规模光伏发电接入系统后如何合理安排的发电机组检修计划、保证电力系统正常运行是一项重要的内容.本文通过在检修计划决策阶段采用分段线性化的方法安排发电机组的发电计划，能有效降低负荷低谷弃光伏发电量，充分利用清洁能源的目的.为考虑大规模光伏电源接入系统后的检修计划优化决策问题，提供了实用的方法.

[1] European Photovoltaic Industry Association Renewable Energy House. Global Market outlook for Photovoltaics until 2013 [ EB/ OL ]. [ 2008 - 04 - 01 ] . http :/ /www. epia. org/.

[2] 赵玉文，吴达成，王斯成，等.中国光伏产业发展研究报告(2006-2007)(下)[J].太阳能，2008,(8):6-13.

[3] 赵春江，杨金焕，陈中华，等.太阳能光伏发电应用的现状及发展[J]．节能技术，2007，25(5)：461-465.

[4] Eshraghnia R，Shanechi M H M，Mashhadi H R.Generation Maintenance Scheduling in Power Market Based on Genetic Algorithm[C]//IEEE:Power Systems Conference and Exposition，2006：1814-1819.

[5] 彭卉，张焰，张彦魁，等.发电机组最佳计划维修周期研究[J].中国电机工程学报，2003，23(7):41-45.

[6] 丁明, 冯永青.发输电设备联合检修安排模型及算法研究[J].中国电机工程学报,2004,24(5):18-23.

[7] Karaki S H,Chedid R B,Ramadan R.Probabilistic Performance Assessment of Autonomous Solar-wind Energy Conversion Systems[J].IEEE Trans on Energy Conversion,1999,14(3):766-772.

[8] Conti S,Raiti S,Tina G,et al.Study of the impact of PV generation on voltage profile in LV distribution networks[J].Power Tech Proceedings, 2001 IEEE Porto 4:10-13.

[9] Wakao S,Takano H,Nakada N,et al.Small-scale distributed PV power generation system of networked composition[C]//Photovoltaic Energy Conversion,2003.Proceedings of 3rd World Conference on Vol.3,May 2003,2298-2301.

[10] 院晓涛.发电机组检修计划优化及其管理系统[D].长沙：湖南大学，2008：12-13.

[11] Suresh K，Kumarappan N.Combined genetic algorithm and simulated annealing for preventive unit maintenance scheduling in power system[C]//IEEE:Power Engineering Society General Meeting，2006:18-22.

[12] Park Young-Soo，Kim Jin-Ho，Park June-Ho，et al. Generating Unit Maintenance Scheduling using Hybrid PSO Algorithm[C]//IEEE:Intelligent Systems Applications to Power Systems，2007:1-6.

[13] 石瑞民，许志刚，孙靖.数值计算[M].北京：高等教育出版社，2004：116-118.

[14] NREL.The Optimization Model for Distributed Power[EB/OL].2011-06-10.http://www.nrel.gov/homer.

[15] Abouzahr I，Ramakumar R.Loss of Power Supply Probability of Stand-alone Photovoltaic System. A Closed Form Solution Approach[J].IEEE Trans on Energy Conversion，1991，6(1):1-11.