一种可应用于大流量环境的双层散列算法研究

张智江，王志军，张 尼

（中国联合网络通信有限公司 北京 100033）

1 引言

散列是信息存储和查询所用的一项基本技术，虽然发明于50年前，其间也有过不少非常系统、完整的研究工作，但近年仍然有新的工作进展。散列技术的基础性及其在许多领域的可应用性是其不断被人们研究的源泉。目前，散列算法已经广泛应用于大流量环境下的工程实践中，典型的场景如骨干网群发邮件过滤[1]、互联网冗余流量清除[2]、移动网络中的短消息过滤[3]等。

一般地，应用于大流量环境下的实时处理系统会面临两个问题：系统需要保留一定数量的历史数据，因此对存储空间有一定的需求（涉及算法的空间性能，如果需要的存储空间过大，系统将难以投入使用）；系统需要对流量数据进行实时查找、比较、修改等操作，因此对操作时间有一定要求（涉及算法的时间性能，如果算法实时性能差，系统难以投入使用）。

直观、常识性的做法是对大流量数据实施散列算法，并将产生的散列值集合存入数据存储结构，便于后续操作。大流量环境下的实时处理系统是否有效、实用，关键就在于如何设计散列算法和对应的数据存储结构以满足系统的时间和空间性能。

[1,2]均希望通过设计一个合理的散列算法同时满足系统的时间和空间性能，但效果却并不理想。本文认为时间与空间性能的需求，可转化成如下两个问题。

·选取合适的散列下标算法（即键值在散列表中的存储位置）。合理的散列下标算法使得键值均匀分布于散列表内各槽中；否则，在槽中查询或添加一个元素会带来较大开销，失去散列表的优越性。

·选取合适的键值。散列表中往往保留原始输入作为键值，以区分槽中存储位置冲突的元素。但是，如果原始键值较长，则不应直接存储和比较，否则必将占用极大的内存空间且耗费时间。

这两种需求是有区别的。前者追求时间性能，要求散列值的分布尽量均匀，查询、比较、修改操作速度快；后者追求算法的空间性能，要求散列表中存储占用空间较小，但能代表原始输入。因此，很难通过一种散列算法同时满足上述需求，参考文献[1,2]只解决了选取键值的问题，使系统具有较好的空间性能，但系统的时间性能较差。

针对上述情况，本文提出一种双层散列算法。两个散列函数均直接作用于原始输入，键值散列函数用于产生可惟一表征原始输入的键值，下标散列函数用于产生键值在数据结构中的存储地址。针对上述两种需求给出了相应的算法评估测度，并通过实验从若干候选算法中选出较优的算法。

2 双层散列算法

2.1 算法思路与数据结构设计

下面以互联网垃圾邮件过滤为例，具体介绍双层散列算法。

将全体邮件集合记作M={M1,M2,…,Mn}，每封邮件的正文部分看成是字节序列的集合{b1,b2,…,bs}。作为研究邮件聚类性质的一个方面，给定k封邮件M1,…,Mk，分析是否存在内容相似性，从而可以聚成同一邮件类，进而识别具有相似内容的群发垃圾邮件。为此，将邮件表示为：

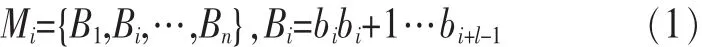
即将每封邮件看成是由连续n个长度为l byte（一般取较大的值，如100 byte）的子序列构成的集合。如果k封邮件M1,…,Mk的交集不为空，则可认为这些邮件内容相似。

一种可行的方法是依次比较邮件中各字节序列是否相同，为提高比较效率，要用数据结构T保存访问过的字节序列Bi。遇到一个元素Bi，先与T中的元素比较，若不在其中，则将它加入T中，否则丢弃此元素，并记录邮件相似情况。显然将T组织成一个散列表是较好的选择。

设双层散列算法中的键值函数为Unique_hash，下标函数为Uniform_hash，hi为原始输入Bi在数据结构中的存储地址，因此有：

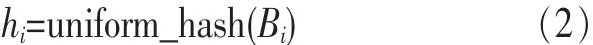
为节省空间，在数据结构中不存储Bi，而是存储可惟一表征 Bi的指纹值 fi，有：

双层散列算法的关键在于选取合适的键值函数及下标函数，以满足实时系统时、空性能。

此外，在处理数据过程中，散列算法需要频繁对内存中存储的大量指纹信息进行检索、比较，为支持上述操作，设计了一套数据结构，由邮件库(MD)和模式库(PD)两部分组成，如图1所示。

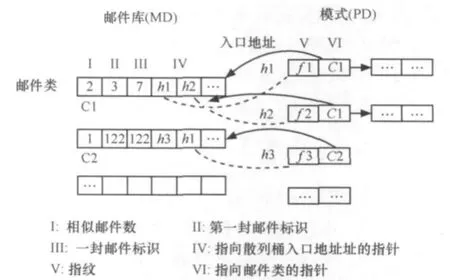
图1 双层散列函数对应的数据结构

· 邮件库以散列表形式组织，保存全部邮件类的描述信息，用于全局统计。描述信息包括所属邮件类的容量、邮件类第一封邮件和最后(即最近)一封邮件的ID、类中邮件指纹信息在模式库中的散列槽地址。

· 模式库以散列表形式组织，负责指纹的保存、检索和组织工作。每个单元对应一个槽，槽内每个元素由一个指纹和该指纹对应的邮件类在邮件库中的入口地址组成。

2.2 算法选择

2.2.1 评估测度

为了比较不同的散列函数的优劣，需要有与应用背景相关的评估测度。对于§1第 1种需求，关心对散列后散列值的平均查询时间；对于第2种需求，关心散列值的冲突情况，保证形成的散列槽中最多只能有一个元素。为此，有下面两种对应的测度定义。

（1）键值函数测度

设有M组内容相似的邮件，每组有Ni封邮件。将邮件中的字节序列用散列函数F形成键值，然后到相应的散列表中查询，假设键值正确命中ni1次，错误命中ni2次，则每组邮件的冲突率为ni1/Ni，查全率为ni1/Ni，有：

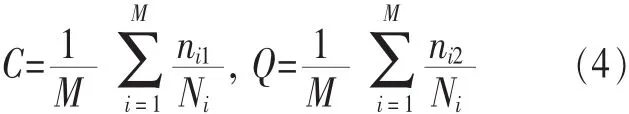
其中，B=C+1-Q，B为键值函数的测度。

（2）下标函数测度

设有N个键值需要处理，将这些键值用散列函数F散列到M个槽中，对于i(1≤i≤M)号槽，散列到其中的键值个数为N。假设查询每个键值的概率是相等的，则对N个键值各作一次查询的时间算术平均值，便可当作F的查询性能测度。按照通常散列表项的链表结构，对i号槽中第k个元素作查询，需要访问存储k次，所以对散列在i号槽中的所有键值都作一次查询，则需要访问存储(ni+1)Ni/2次。考虑所有的槽，可以用平均存储访问次数表示散列函数F的查询性能测度，即：

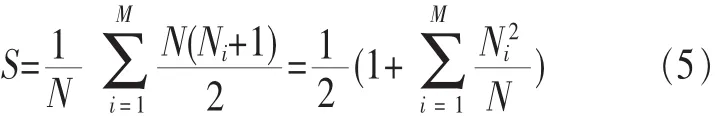
S即为下标函数的测度，其值越小越好。

根据上述条件和凹函数的基本性质，当Ni=N/M时S取最小值，当只有1个Ni=N，其他Ni为0时取最大值，两个极值分别为N/(M+1)/2、(N+1)/2。

2.2.2 待评估的散列函数

（1）用于生成键值的候选函数

Rabin指纹算法[4]是公认的最优键值函数，其键值长度为64位，值域范围大，可代替原始输入而不产生冲突，因此将Rabin指纹算法作为惟一的候选函数，算法实现如图2所示。

图2 Rabin指纹算法实现

（2）用于生成下标的候选函数

考虑3个候选函数：Rabin指纹算法，实现简单且与键值算法联系紧密；Unix System V中的散列函数UV5 Hash，被称为“实际生活散列函数中的典型魔术”[5]，但对URL的处理性能不好；应用于天网搜索引擎的折叠函数Hflp[5]，被称为处理URL的查询速度和负载平衡效果最好的函数。下标候选函数算法实现如图3所示。

2.3 实验验证

从某运营商骨干网边界路由器的一条链路上采集数据，数据仅包含双向SMTP流量，并以Tcpdump格式进行文件保存。其中邮件流量1捕获于2009年，包含28 488封内容完全相同的邮件，已经做好标记；邮件流量2捕获于2010年，包含邮件近100万封，最多4 000万个字节序列作为背景流量。实验的目的是选取具有较优时空性能且能识别群发邮件的函数。流量1、2由于捕获时间相隔较远，保证内容不会发生干扰。

图3 下标候选函数算法实现

图4 键值性能

将流量1、2混合回放，首先对键值的惟一性进行测试。取散列表槽数M=400万，以100万为间隔，以N=100万，200万，…，4 000万个字节序列为原始输入，通过测度1测试Rabin函数。

键值性能如图4所示，Rabin指纹算法性能稳定，实验中始终保证为原始字节序列生成惟一的键值，因此可代替原始输入保存在散列表中。

图5 下标函数性能比较

对下标函数进行测试，分别取散列表槽数M=50、100、400、1 600(单位:万)，以 100万为间隔，以 N=100 万，…，4 000万个键值为输入，通过测度2测试3个候选函数。性能对比如图5所示。

由图5可以看出，UV5 Hash具有绝对的优势，在所有情况下都是最佳选择。此外，随着槽数减少，UV5变化不大，始终保持较好的性能。这表明，UV5表现优异而且相当稳定。槽数不变时，Rabin函数的性能在键值数量较少的情况下与HfIp相当；但随着键值的增大，Rabin函数的性能显著下降。

特别地，当将槽数减少到20万时，Rabin函数查询4 000万键值用时超过20 h，已经无法使用；而UV5和Hlfp算法性能基本相当，并保持400 000键值/秒的处理速度。这表明UV5与Hflp均可应用于内存有限的大流量环境中，而Rabin函数不应使用。

本文结论与参考文献[5]不同，在本文中，UV5 Hash是最优的下标散列函数，Hflp函数次之，Rabin函数不适合作下标散列函数。实验表明，在散列表槽数较大的情况下，Hflp甚至不如Rabin函数，这个差异可能与两者的原始输入特点有关。

3 结束语

本文提出一种可应用于大流量环境的双层散列算法。实验表明，本方法实用且有效，网络管理人员可将此算法应用于大流量环境，以减少网络中冗余流量、过滤垃圾邮件及进行流量分析。

参考文献

1 Zhang N,Jiang Y,Fang B X.Traffic classification-based spam filter.In:Proc of ICC’06,Istanbul,Turkey,June 2006

2 Spring N,Wetherall D.A protocol-independent technique for eliminating redundant network traffic. In:Proc of ACM SIGOCOMM,Aug 2000

3 黄文良,张尼,董玉涛.基于移动终端位置和发送内容的垃圾短信监控方案.移动通信,2008,32(13)

4 Manber U.Finding similar files in a large file system.In:Proc of USENIX Winter Technical Conference,Jan 1994

5 李晓明,凤旺森.两种URL散列效果很好的函数.软件学报,2004,15(2):179～184