磁场调制式磁力齿轮及其有限元计算

杜世勤

（上海电机学院 电气学院，上海 200240）

磁场调制式磁力齿轮及其有限元计算

杜世勤

（上海电机学院 电气学院，上海 200240）

为避免机械齿轮振动，或要在分开物体间传递力矩，可以采用磁力齿轮传动装置。设计该磁力传动装置时需要对其设计参数进行精确计算。在电机设计时，使用有限元方法对一种大力矩磁力齿轮——磁场调制式磁力齿轮进行了磁场计算，为设计该磁力齿轮提供了有力的工具。

磁场调制；磁力齿轮；有限元方法

随着电气时代的到来，电力传动在传动领域中的地位越来越重要。但是，从经济性和减小设备体积的角度考虑，在许多实际应用场合要实现直接电力传动并不现实，因此机械齿轮仍有着广泛的应用。通过齿轮箱两端连接主传动轴和负载，虽然解决了速度和转矩的匹配问题，但也带来诸如振动、噪声等机械齿轮自身难以克服的问题。

随着对稀土永磁材料尤其是钕铁硼（Nd－FeB）材料研究的发展，稀土永磁材料越来越受到人们的重视，其不仅在电机传动领域得到应用，也被应用于其他机电设备与传感器中。这些磁体可有效地应用于大空气间隙的磁力耦合装置中。

磁力传动的研究成果可追溯至1943年，当时首项知名专利在英国被授予给了霍华德兄弟。磁力驱动泵的早期工业开发由霍华德机械发展有限公司在20世纪40年代末首创［1］。磁力传动在离心泵上的应用极为成功。利用磁体吸引铁磁物质及磁体，或磁场之间有磁力作用而非铁磁物质不受其影响或很少影响磁力的大小的特性，可无接触地透过非磁导体（隔离套）进行动力传输，这种传动装置称为磁性联轴器。电动机通过联轴器与外磁钢联接，叶轮与内磁钢联接。在外磁钢和内磁钢之间设有全密封的隔离套，将内、外磁钢完全隔开，使内磁钢处于介质之中，电动机的转轴通过磁钢间磁极的吸力直接带动叶轮同步转动。磁力泵以静密封取代动密封，使泵的过流部件处于完全密封状态，彻底解决了其他类型泵使用机械密封无法避免的跑、冒、滴之弊病。

早在1913年，美国就有了磁力齿轮的相关专利申请［2］，但是磁力齿轮的研发一直没有进展，主要是因为早先的永磁材料性能较差，同时在结构设计方面也没有突破，导致磁力齿轮的转矩传递密度较低，磁力齿轮传动装置的用途不大。目前，磁力传动机构利用磁场进行转矩传递，其转矩输入端和输出端是非接触性的，故可以从根本上克服机械齿轮的缺点。

1 常用磁力传动机构

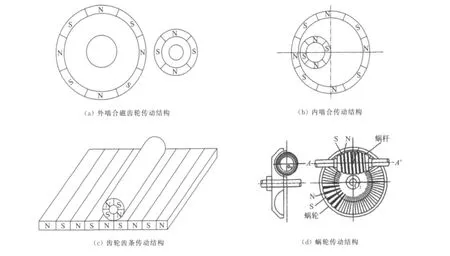
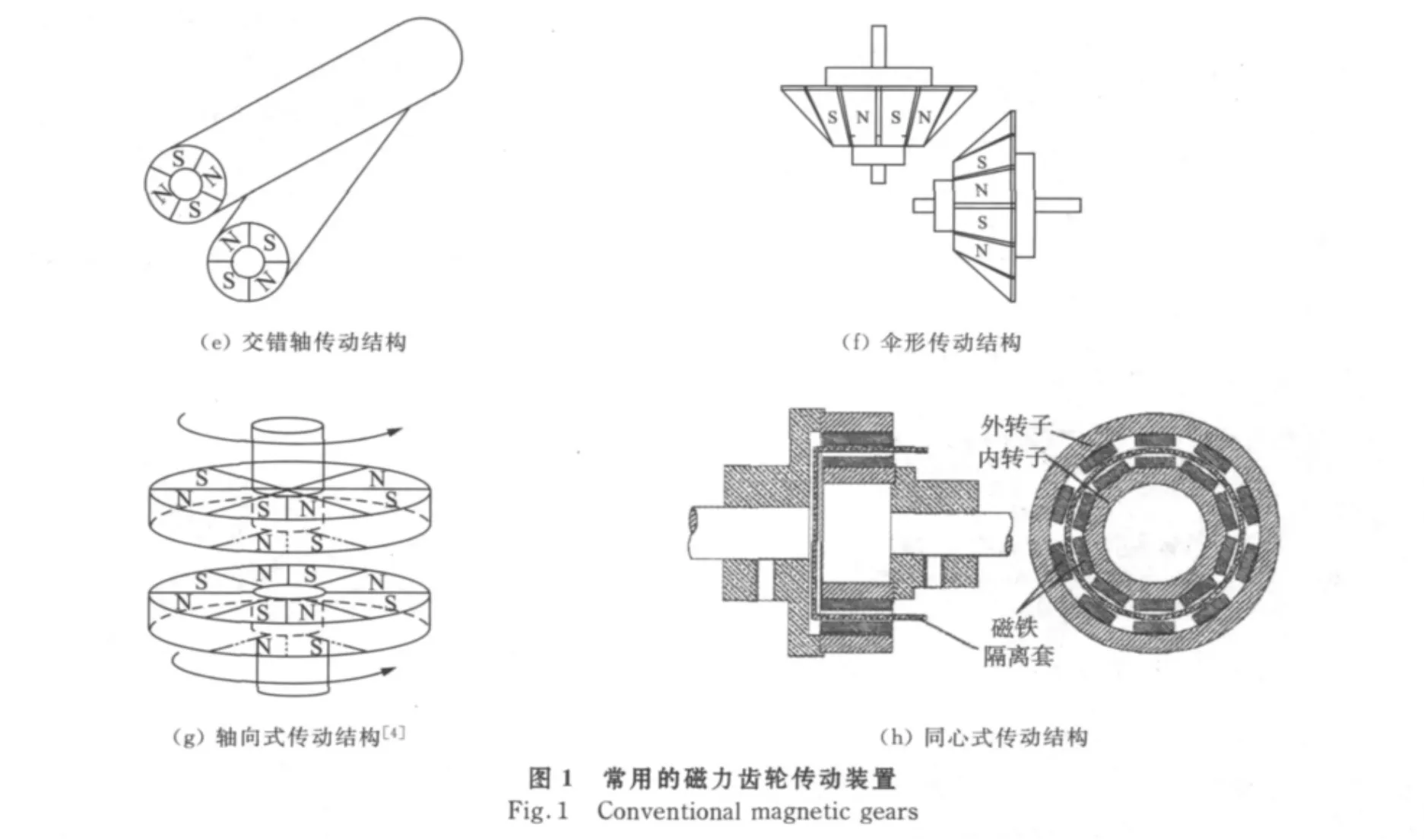
目前，永磁材料性能已经有了很大提高。第3代稀土永磁材料——NdFeB磁钢在室温下剩余磁感应强度B可达到1.47T，磁感应矫顽力Hc可达992kA／m（12.4kOe），最大磁能积（BH）max高达397.9kJ／m3（50MG·Oe）［3］；因此，随着计算技术的发展，磁力齿轮的研究也活跃起来。图1给出了8种不同的磁力齿轮传动装置，其中前6种磁力齿轮受到拓扑结构的限制，永磁体利用率较低；后2种为磁力联轴器，为了提高转矩密度，尽可能多地使用了永磁材料。

为了得到可控的磁力传动，各种不同结构的电磁离合器装置也应运而生，并被广泛应用于实现机械传动系统中原动机与工作机间、机械内部主动轴与从动轴间的运动、动力的传递与脱离。

永磁齿轮传动分外啮合传动、内啮合传动、齿轮齿条传动、蜗轮传动、交错轴传动结构、伞形传动结构、轴向式传动和同心式传动，如图1所示，它们适用于不同的场合。

2 磁场调制式磁力齿轮

文献［5－6］中提出了一种新型结构的磁力齿轮（见图2），克服了传统磁力齿轮传动扭矩小的缺点，也为磁力齿轮的研究提供了一个新的切入点。从结构上，该磁力齿轮主要由3部分构成：内部是具有较少磁极的内转子（高速转子），外部是具有较多磁极的外转子（低速转子），中间固定部分是由高导磁材料和非导磁材料交错组成的齿形定子（调磁环），起到调制内、外转子磁场的作用。由于该新型磁力齿轮的基本工作原理是依靠齿形定子（调磁环）对磁场进行调制，故本文将其称为磁场调制式磁力齿轮。

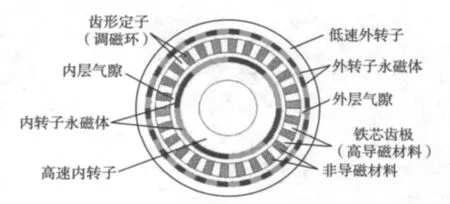
图2 磁场调制式磁力齿轮传动装置Fig.2 Field modulated magnetic gear

由图2可见，磁场调制式磁力齿轮的内、外转子为同心式结构，在转矩传递过程中所有的永磁体都参与转矩传递，有效地提高了永磁体的利用率，故其转矩密度可以比传统磁力齿轮高出很多。在此基础上，中、英、德、美、丹麦等国科研人员进一步开发出各种新式的磁力齿轮［7-13］。

本文提出了该新型磁力齿轮传动装置的一种实现结构，图3为其装配图，其中磁力齿轮的结构如图2所示，包括外转子、内转子和它们中间作为齿形定子的调磁环。在该实例中，高速的内转子和低速的外转子都采用表面式磁钢，高速的内转子是4对极，低速的外转子是17对极，调磁用的齿形定子的铁心齿极数是21个。外转子、内转子铁心部分和齿形定子（调磁环）中的铁心齿极采用导磁硅钢片叠压构成。设计时，4与17以及17与21的最小公倍数相对较大，这样齿槽定位转矩就会小些。

磁场调制式磁力齿轮传动装置运作的基本原理在于使用了导致气隙磁导变化的齿形定子（调磁环），调制了两边转子上永磁体产生的磁场，使调制好的磁场具有的谐波与对面转子上的永磁体相互作用。

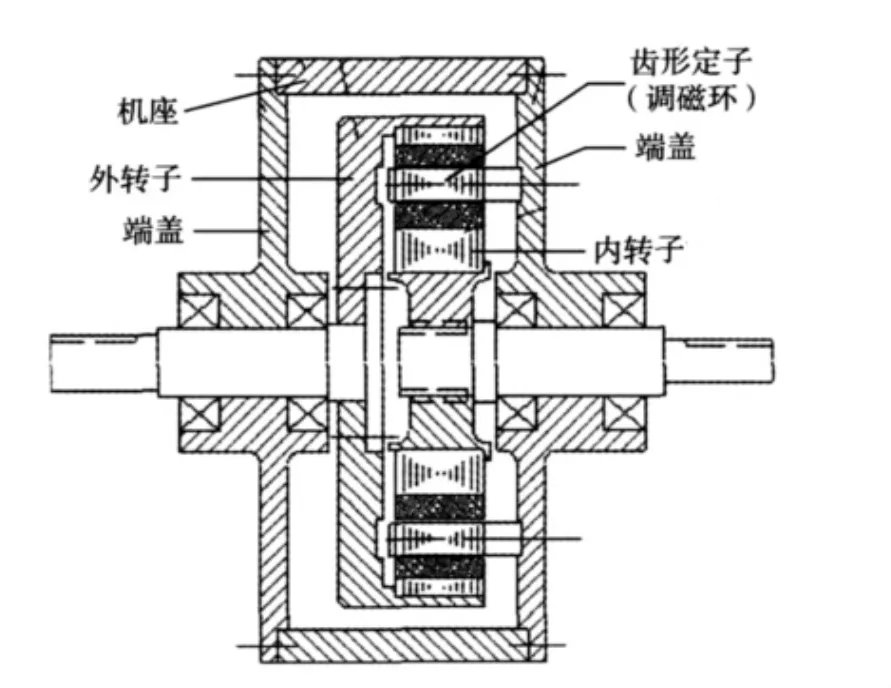
图3 磁场调制式磁力齿轮装配图Fig.3 Structure of field modulated magnetic gear

3 磁场调制式磁力齿轮的有限元方法计算

有限元法是获取数理方程边值问题近似解的有效数值计算技术，解决了很多的难题。在电机的电磁计算中，无论是电机结构的改变、材料的变化，还是定转子上的激励的变化，都能使用有限元方法进行计算。相对于解析方法的局限性，有限元方法有较大的使用范围，而且随着计算技术的发展而不断发展［14］。有限元计算技术的有效性已被无数次的工程应用所证实［15］。

使用有限元进行数值计算总是按步骤进行的。先进行网格剖分，可应用各种不同的网格形状，即使在同一求解区域，不同的网格形状也可同时使用。对于要分析的装置，其有限元模型包含的信息有几何剖分、材料、激励和约束条件等。材料特性、激励和约束条件容易用信息化方式表达，但几何形状较难表述。有限单元可以非常微小且细节化地呈现，如气隙部分要求剖分得很小，而其他部分则没有这么高的要求。

具体到磁场调制式磁力齿轮的磁场计算，旋转式磁力齿轮的内转子、外转子和调磁环在几何上具有对称性，有时磁场分布呈现出周期性，这就给使用计算机对其进行几何建模和物理建模提供了方便，减少了计算程序的参数输入，磁场计算也不易出错。对于大小不同的同类型磁力齿轮的磁场计算，只需简单地变换相应数据便可，实现了参数驱动。用好几何结构上对称性的前提是在设计该磁力齿轮时熟悉调磁环形状、永磁磁极结构，进而对点成线、线成面具有清楚的映像。

基于点连成线、线形成面的原理，节点、线段和基本子域的编号如图4所示。图4（a）中，内转子、外转子及调磁环区域标号用汉字表示，节点标号用数字表示。图4（b）中，线段、弧用数字标号，箭头指向方向。

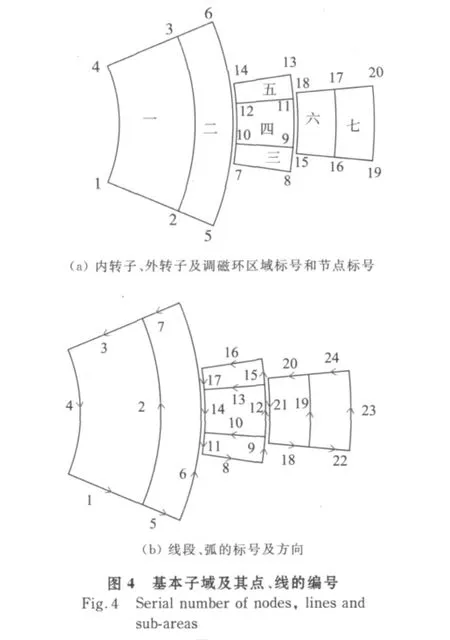
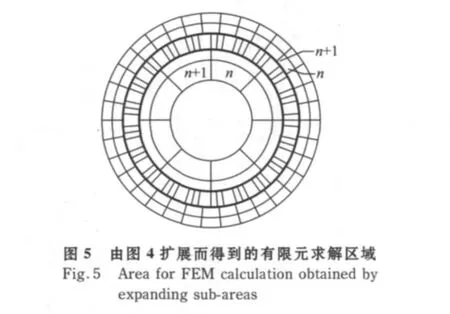
若要有所有计算子域的信息，还应将上述基本子域扩展，形成一个完整的有限元计算场域的几何和物理信息。本文中将图4扩展至图5。图5为一个完整的有限元计算场域。

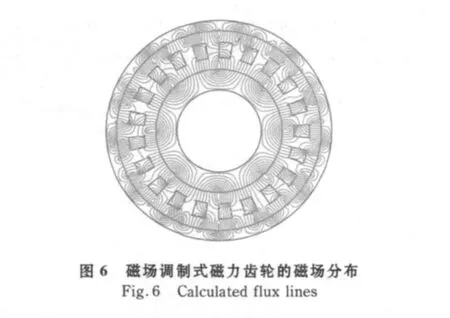
对图5对应的几何区域进行有限元剖分，结合相应的物理信息，计算得出磁场调制式磁力齿轮的磁场分布，如图6所示。在此基础上可进一步优化该磁力齿轮的设计。

4 结 语

稀土永磁材料在机电产品中的应用越来越受到人们的重视。与传统机械联轴器、机械齿轮相比，稀土永磁磁力耦合器与稀土永磁齿轮在许多应用场合都具有优越性。通过理论学习，一种具有很高的转矩密度的磁场调制式磁力齿轮已完成设计，并使用业界通用的有限元方法计算了该磁力齿轮的磁场分布。

［1］Twyford D.英国HMD公司无泄漏磁力驱动泵的开发与研制［J］.化工装备技术，1997，18（3）：50－53.

［2］Rasmussen，P O，Andersen T O，Jørgensen F T，et al.Development of a high－performance magnetic gear［J］.IEEE Transactions on Industry Application s，2005，41（3）：764－770.

［3］唐任远.现代永磁电机理论与设计［M］.北京：机械工业出版社，1997.

［4］严晓霞，赵朝会，张 迪，等.2种磁力耦合器性能的比较［J］.上海电机学院学报，2009，12（4）：289－292.

［5］Atallah K，Howe D.A novel high－performance magnetic gear［J］.IEEE Transactions on Magnetics，2001，37（4）：2844－2846.

［6］Atallah K，Calverley S D，Howe D.Design，analysis and realisation of a high－performance magnetic gear［J］.IEE Proceedings－Electric Power Applications，2004，15（2）：135－143.

［7］Atallah K，Wang J，Howe D.A high－performance linear magnetic gear［J］.Journal of Applied Physics，2005，97（10）：10N516.1－10N516.3.

［8］Mezani S，Atallah K，Howe D.A high－performance axial－field magnetic gear［J］.Journal of Applied Physics，2006，99（8）：08R303.1－08R303.3.

［9］Frank N W，Toliyat H A.Gearing ratios of a magnetic gear for marine applications［C］／／2009IEEE Electric Ship Technologies Symposium.Baltimore，MD：IEEE，2009：477－481.

［10］Hafla W，Buchau A，Rucker W M，et al.Efficient design analysis of a novel magnetic gear on a high performance computer［J］.The International Journal for Computation and Mathematics in Electrical and Electronic Engineering，2007，26（3）：712－726.

［11］Jørgensen F T，Andersen T O，Rasmussen P O.The cycloid permanent magnetic gear［J］.IEEE Transactions on Industry Applications，2008，44（6）：1659－1665.

［12］Liu Xinhua，Chau K T，Jiang J Z，et al.Analysis of concentric magnetic gears using three dimensional scalar magnetic potential finite element method［C］／／IEEE International Magnetics Conference.Madrid，Spain：IEEE，2008：AL－04.

［13］Li Yong，Xing Jingwei，Peng Kerong，et al.Principle and simulation analysis of a novel structure magnetic gear［C］／／International Conference on Electrical Machines and Systems.Wuhan：IEEE，2008：3845－3849.

［14］屠关镇，电机磁场有限元新技术［J］.电机技术，2007（2）：1－4.

［15］Salon S J.Finite element analysis of electrical machines［M］.Boston：Kluwer Academic Publishers，1995.

Field Modulated Magnetic Gear and Calculation Using Finite Element Method

DU Shiqin
（School of Electrics，Shanghai Dianji University，Shanghai 200240，China）

Magnetic gears can be used in place of mechanical gears to reduce undesired vibrations and for applications that require torque coupling between separated members.The design of the electromagnetic devices requires accurate calculation of the design parameters.This paper deals with a field modulated magnetic gear and its calculation with the finite element method，and provides a powerful numerical technique for designing magnetic gears.

field modulation；magnetic gear；finite element method（FEM）

TM 301

A

2095－0020（2011）03－0173－05

2011－04－17

国家高技术研究发展计划（863）项目资助（2007AA05Z233）；上海市教育委员会重点学科资助（J51901）

杜世勤（1967－），男，讲师，工程师，博士，专业方向为电磁计算和电机控制，E－mail：dusq＠sdju.edu.cn