重载列车组合站通过能力计算方法研究
张进川,杨 浩,刘 博,魏玉光
(北京交通大学 交通运输学院,北京 100044)
重载列车组合站通过能力计算方法研究
张进川,杨 浩,刘 博,魏玉光
(北京交通大学 交通运输学院,北京 100044)
根据重载列车组合站的特点,分析车站站型、列车在站作业特点和列车在站作业过程等,探讨影响重载列车组合站通过能力的主要因素,明确基于实现概率的组合站通过能力的含义,提出重载列车组合站通过能力的计算方法。以计算机仿真为手段,建立重载列车组合站通过能力仿真模型,制定了仿真实现策略,并以湖东站为例进行了验证。
铁路;重载列车;组合列车;通过能力
对于大宗物资运输通道的重载铁路,由于其货流来源与去向的多样性,往往需要开行组合式重载列车,即为了提高重载铁路的输送能力,采取措施提高重载干线的列车牵引定数。由于相应集疏运线路的列车牵引定数相对较低,因此需要在技术站 (重载列车组合站)将若干列小编组列车 (小列) 组合为大编组列车 (大列)再进行直达运输。
1 重载列车组合站的特点
影响组合列车开行规模的因素包括装卸车能力、机车车辆性能、供电能力、区间通过能力和组合站通过能力等。其中,由于专业的重载列车组合站是新生事物,现行车站能力计算方法中尚无明确的关于重载列车组合站通过能力的计算理论与方法,因此研究重载列车组合站通过能力是合理利用重载铁路运能的重要课题。
1.1 重载列车组合站站型
重载列车组合站站型布置与普通编组站相比,车站作业过程简单,没有大量的解编作业,主要是负责重载列车的组合分解作业,因此车站到发线有效长较长,一般满足2万吨列车组合作业的到发线有效长需达到 2 800 m,满足1万吨列车组合的到发线有效长需达到 1 700 m。为了叙述方便,将用于组合列车作业的到发线称为组合到发线,由组合到发线组成的车场称为组合到发场,其余称为普通到发线和普通到发场。为方便列车到达、组合、分解作业过程中机车的出入库,到发线和机走线间设置腰岔,如图1所示。
1.2 重载列车在组合站的作业特点分析
重载列车组合站主要是接发单元列车和组合列车。单元列车在车站的作业比较简单,只需要进行技检或机车换挂、乘务组的换班等。组合列车在车站的作业大致分为3个阶段:列车到达、列车组合、列车出发。编组站和重载列车组合站的列车在站作业过程如下。
(1)编组站的列车作业过程。到达作业:一条到发线只允许接入一列列车。解体作业:大量的车列解体作业,驼峰作业量较大。集结作业:车列集结过程复杂,集结车组数目大小不均。编组作业:列车编组形式多样,利用牵出线编组列车。出发作业:列车出发占用道岔咽喉时间短,出发时间间隔较小。
(2)重载列车组合站的列车作业过程。到达作业:列车进站占用咽喉时间较长,同一条到发线允许连续接车。组合作业:主要是大列间的集结,集结需要的车组数目少;组合形式比较简单,由5 000 吨列车、万吨列车组合成万吨列车和2万吨列车;列车在到发线上组合;车站的驼峰解体作业量较少,利用率不高。出发作业:列车出发占用咽喉时间长,出发时间间隔较大。
2 基于实现概率的重载列车组合站通过能力
2.1 组合站通过能力的影响因素
在实际工作中,由于车站能力受外部环境因素、设备因素、车流因素和组织管理因素等的影响,这些日常作业的不确定性对重载列车组合站通过能力有较大的影响,如列车不均衡到达造成短时间内运输供给的波动等日常作业不规律性造成的影响[1]。影响重载列车组合站通过能力的主要因素是车站固有技术设备情况、车流构成和数量、列车到发的均衡性、到发线的空费时间、车站列检能力和机车运用模式等。
2.2 组合站通过能力实现概率的含义和计算方法
车站通过能力是固定设备、活动设备和组织管理有机结合的产物,在计算时不仅要考虑各种运输设备的数量、时空配置、运营特点和生产过程的组织管理,而且要考虑各种变化条件下能力的可实现性。即车站通过能力水平不仅取决于各设备间的相互作用、相互制约的关系,而且取决于活动设备对车站设备的占用频率、延续时间和先后顺序关系等,因此车站通过能力据有某种不确定性。
在给定的各项设备及运行条件下,重载列车组合站在给定时间内完成的组合量记为 X,则 X 是一个随机变量。由于在给定时间内完成并输出的组合量是一个大于等于0的整数,所以该变量是一个离散型随机变量,其分布应为:

式中:xk为组合量的第 k 个可能值,列;Pk为组合量是 xk的概率。
定义重载列车组合站通过能力的实现概率为:在给定的各项设备、运行条件和时间单元内 (通常为一昼夜 24 h),重载列车组合站完成并输出的组合量达到或超过给定目标组合量的概率。由概率的可列可加性[2],实现概率可表示为:

3 基于实现概率的重载列车组合站通过能力计算模型
计算车站通过能力主要有3种方法:分析计算法、图解计算法和计算机仿真法。
目前,计算机仿真法是计算车站能力较常用的一种方法。该方法是在对铁路运输能力的概念和理论基础上,总结车站作业人员制定和实施车站技术作业的实践经验,建立作业组织规则及相应的组织机制和调整体制,通过对影响车站作业能力的设备因素、车流因素和组织管理的复杂相互关系进行追踪,实现对车站设备利用和作业组织的全方位模拟。计算机仿真法主要采用的是系统工程、随机理论和计算机仿真技术相结合的方法,综合利用了理论分析、思维分析和模拟数据分析等方法。
重载列车组合站仿真系统在每个仿真周期内都要遍历路网中每列车的详细情况、进行相应作业等,每一列车的仿真过程如下。
步骤 1:仿真系统随机产生一列列车。
步骤 2:列车进入进站咽喉区域,判断列车种类,如为待组合列车,转到步骤 3;否则,列车进入普通到发场区域,转到步骤 5。
步骤 3:列车进入组合到发场区域,判断组合到发线占用状态,若到发线后半段空闲且该列车到站与到发线前半段占用列车到站相同,则列车进入到发线后半段,转到步骤4;否则,列车接入组合到发线的前半段,转回步骤 1。
步骤 4:对组合到发线上的两列车进行组合作业,组合作业时间根据概率分布随机产生,列车数量减1。
步骤 5:列车进行相关技术作业,作业时间根据分布随机产生。
步骤 6:列车通过发车咽喉区域进入出站区间,列车数量减 1。
在每一仿真周期内,对仿真路网系统内的列车状态进行全部判断之后,仿真时钟步长向前推进,最终达到预定的仿真总时间之后,仿真结束。
4 湖东站通过能力计算及结果分析
根据大秦铁路湖东站重车场的车站配置图、车流及作业组织办法等,依照上述仿真思想、模型和方法,对湖东站的通过能力进行了仿真计算。
主要针对2列万吨列车组合为1列2万吨列车的组合作业进行实验仿真,仿真周期为 24 h。每次仿真开始前,随机生成列车到达时间,列车到达时间是依照现场统计的数据确定,在仿真程序开始运行之前,事先生成一定数量的列车到达时间表,仿真时依次读取。当到达列车为到达某股道的第一列车时 (停在股道前半段),则等待第二列车的到达;当到达列车为到达某股道的第二列车时,即可进行组合作业,作业时间根据概率分布随机产生。其仿真程序如图1所示。
根据 2006 年对湖东站现场列车作业的写实情况,列车在车站的到发数据及作业时间分布情况如下。
(1)列车到达时间间隔分析。列车到达的平均时间间隔为 624 s,通过采用统计软件分析,列车到达时间间隔基本服从正态分布。
(2)列车组合作业时间。根据现场写实数据,自中部机车入线至2万吨列车组合完毕平均用时为25.6 min,其中最短时间为 10 min,最长时间为 54 min。通过采用统计软件对数据分析可知,数据大致服从正态分布。
(3)根据车站现场统计的各项作业交叉干扰情况。由交叉干扰引发的干扰时间近似服从正态分布,最小为 2 min,最大为 40 min,平均干扰时间为 12 min。
在仿真站内列车作业时,引入随机交叉干扰,仿真过程中将车站可能发生的各种交叉干扰转化为对作业时间的影响,在给定作业时间的基础上加上干扰时间[3]。因此,确定自第二列列车到达至2万吨列车出清股道时间:平均用时为 161 min,其中最短时间为 68 min,最长时间为 330 min。通过采用统计软件分析,数据基本服从 γ 分布,其两个参数α、β分别为α=8、β=0.05。
湖东站2万吨列车到发线数量为6条,需考虑列车组合作业的能力限制;而万吨列车的到达场和2万吨列车的直通作业不考虑能力限制。根据未来列车的主要去向,将组合列车设为3个去向 (曹妃甸、柳村南、其他),其比例为 2:2.2:1;模拟时扣除车站天窗影响时间 120 min。每次仿真时给定的行车量足够大,设定仿真时间 30 h,得到后 24 h 内每次仿真能够通过的行车量。不同行车量条件下的模拟结果如表1所示。
由表1可以看出,随着行车量的增加,实现概率逐步减小,而且在临界状态时迅速下降,如图 2所示。
根据模拟分析,假设车辆静载重为 0.8,一年按 365 天计算,不考虑其他影响因素,在一定实现概率条件下湖东站的通过年运量如表2所示。
经分析可知,运量达到 3.7 亿 t 左右时,在既有设备条件下,湖东站能力利用基本饱和,如需进一步扩能,需要从设备改造或改善车流结构,即增加直通2万吨重载组合列车的数量方面考虑。
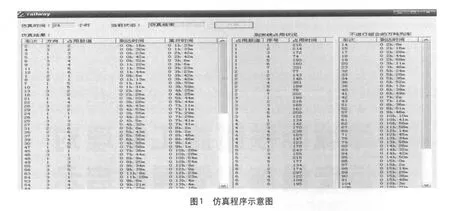

表1 不同行车量下的模拟结果

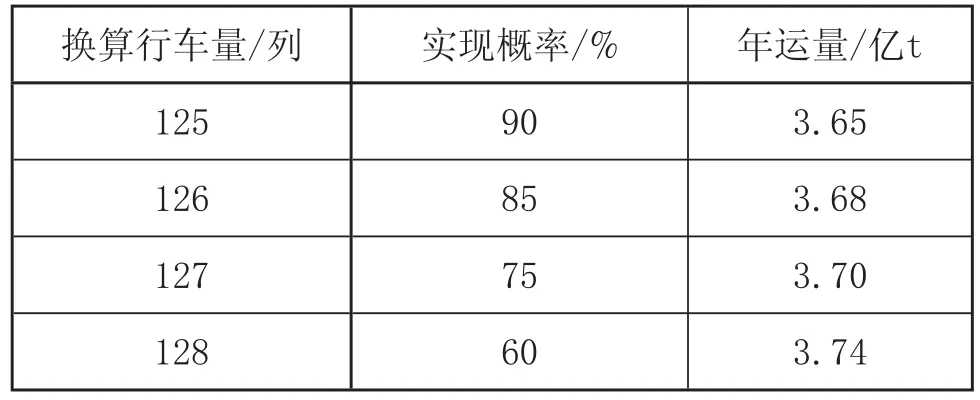
表2 一定实现概率条件下湖东站的通过年运量
[1] 齐新宇. 车站通过能力模拟分析系统研究[D]. 北京:北京交通大学,2000.
[2] 盛 骤,谢式千,潘承毅. 概率论与数理统计(第四版)[M].北京:高等教育出版社,2008.
[3] 杨肇夏,李 菊. 铁路编组站技术作业模拟系统的研究[J].铁道学报,1996,18(4):25-32.
1003-1421(2011)02-0006-04
U292.5+1;U292.3+7
B
2010-09-27
铁道部科技研究开发计划项目(2009X011-C)
责任编辑:林 欣

