力觉交互系统稳定性研究

张玉茹 王党校 戴晓伟 吴 俊 于 歌

张玉茹 工学博士 教授 100191 北京市 北京航空航天大学 机械工程及自动化学院 yuru@buaa.edu.cn

王党校 工学博士 副教授 100191 北京市 北京航空航天大学 机械工程及自动化学院 hapticwang@buaa.edu.cn

戴晓伟 博士研究生 100191 北京市 北京航空航天大学 机械工程及自动化学院 daixw@me.buaa.edu.cn

吴 俊 博士研究生 100191 北京市 北京航空航天大学 机械工程及自动化学院 wujun@me.buaa.edu.cn

于 歌 博士研究生 100191 北京市 北京航空航天大学 机械工程及自动化学院 yuge@aspe.buaa.edu.cn

1 引言

力觉交互(Haptic Interaction)是人机交互领域一个十分活跃的研究方向，如同听觉交互和视觉交互，其基础性和重要性日益受到重视。力觉交互技术应用前景广阔，对产品设计、手术仿真、健身康复、娱乐教育等涉及经济发展和社会生活的多个方面可能产生重要影响[1-4]。

力觉交互系统(Haptic Interaction System，HIS)由虚拟环境、力觉交互设备和操作者等3部分组成(见图1)。操作者通过力觉交互设备感知虚拟环境的力信息，例如虚拟物体质量、惯性力和接触力等。

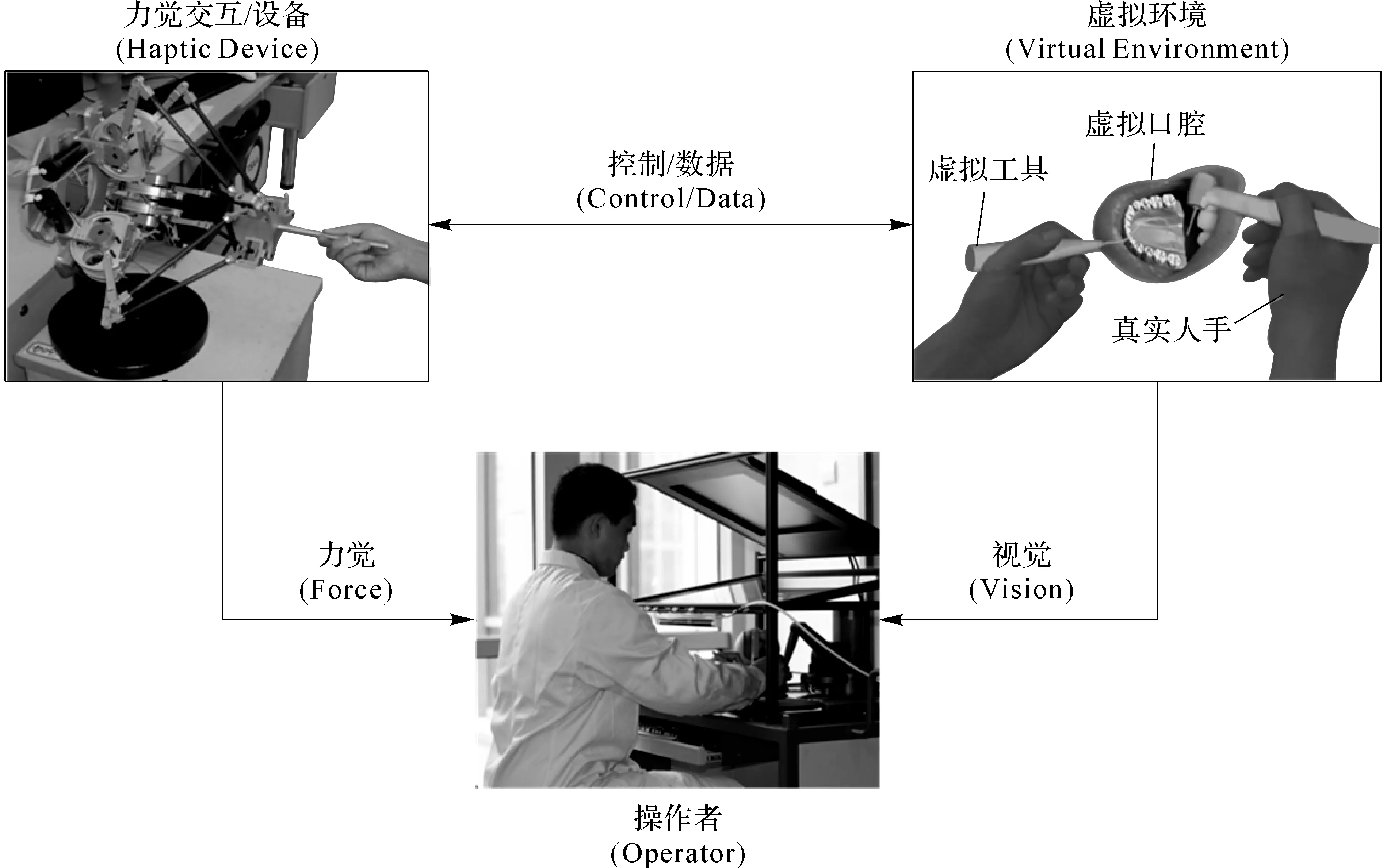
图1 力觉交互系统组成

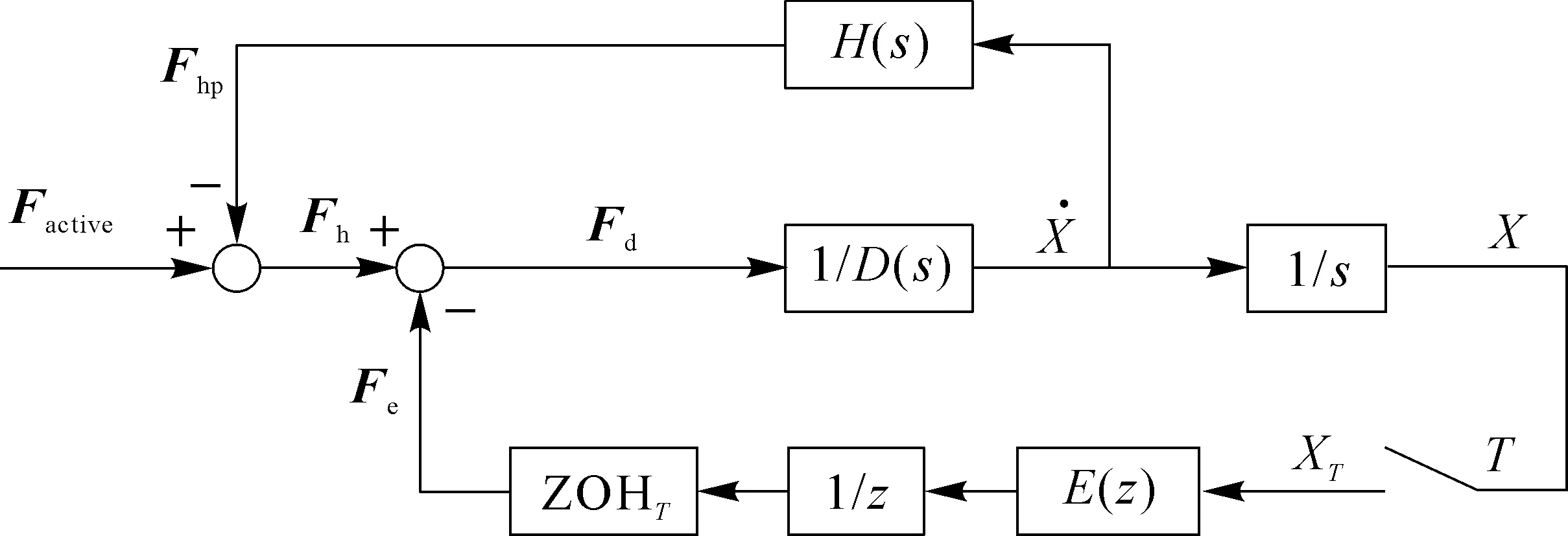
图2表述了力觉交互系统(HIS)的一种信号流动关系，其中位置信号X(t)和力信号F(t)在操作者和交互设备之间是连续信号，在交互设备与虚拟环境之间为离散位置信号X(k)和离散力信号F(k)。由于力觉交互设备的振动将严重影响力觉信息的准确传输，降低仿真系统的逼真度，不利于操作者安全[2]，因此，稳定性(Stability)是力觉交互系统(HIS)的一个重要且基础的指标。

图2 力觉交互系统控制信号流程

交互设备的振动是影响仿真系统逼真度的一个主要障碍。为了解决这一问题，北京航空航天大学张玉茹研究团队在中国国家自然科学基金资助项目《牙科手术模拟力觉交互系统稳定性研究》和《基于双模式力觉交互的灵巧动作技能训练方法研究》，以及中国国家高技术研究发展计划(863计划)项目《面向手眼协调操作的触(力)觉合成和视觉-力觉融合再现技术》的共同支持下，围绕虚拟操作系统的稳定性条件(stability condition)，研究了力觉交互系统(HIS)的稳定性，探索提高逼真度(fidelity)的有效方法，为开发高性能牙科手术模拟训练系统(High Performance Dental Training System)提供理论依据和关键技术。

与传统机器人系统相比，力觉交互系统(HIS)有两个显著特征，一是操作者与交互设备接触，其行为方式直接构成对交互设备的约束；二是虚拟环境是离散系统，而操作者所在的物理环境是连续系统。因此，力觉交互系统(HIS)是离散与连续的耦合。

上述两个特征代表了力觉交互系统(HIS)稳定性研究的特殊性和复杂性。这种特殊性和复杂性带来的科学问题有二，一是人在控制回路中，其动力学行为如何描述尚不清楚；二是力觉合成的计算过程复杂，稳定性建模分析没有现成的方法。

采用经典控制理论(例如Nyquist稳定性判据)解决力觉交互系统(HIS)稳定性问题，需要建立人的行为动力学模型，但目前尚缺乏成熟的理论。近年来，有学者从心理学角度研究人对交互设备振动的感知[5]，这些研究的深入对于建立人的行为动力学模型将有可能产生作用。因此，目前仍然采用传统动力学模型(例如，假设操作者是二阶线性时不变系统)描述人的行为，研究力觉交互系统(HIS)稳定条件，其假设的准确性和实用范围有待更广泛的实验验证。

另一种研究思路是从被动性假设(passivity assumption)出发，提出鲁棒控制算法，避免对操作者进行建模[6-8]。Colgate[3]较早关注到力觉交互系统(HIS)的稳定性，首先基于被动性假设研究了一自由度交互设备的情况，考虑的虚拟环境是一个解析表达的单边约束，称为虚拟墙(Virtual Wall)，并且用弹簧阻尼模型计算虚拟物体与虚拟墙接触时的交互力。Colgate建立的系统模型虽然简单，但却得到了一些重要的研究结论，对于设计力觉合成算法和交互设备具有指导意义。Colgate发现被动性对保证系统鲁棒性是非常有效的，但它只是充分条件。此外，即便是像虚拟墙这样简单的虚拟环境，操作者的行为变化，也会导致系统不稳定，这说明人的行为在实际应用系统中是不可忽视的重要因素。Adams[9]等学者假设操作者为被动，且虚拟环境为线性被动，基于被动性理论和线性电路理论来分析稳定性，给出了系统绝对稳定的判定条件。Miller[8,10]等学者基于能量传递理论和被动性补偿方法，分析虚拟环境为非线性的、非被动时的力觉交互系统(HIS)稳定性条件。Mahapatra[11]等学者采用混合系统的被动性的思想来分析动力学属性演变的虚拟环境下力觉交互的稳定性。Gil[12]等学者基于特征方程方法，采用Routh-Hurwitz判据来分析系统稳定性。

被动性假设是目前研究稳定性的主要方法，其好处是避免对操作者这一复杂对象进行建模，还可以将虚拟环境看作一个黑箱，通过其与交互设备之间的能量传输和被动性补偿来判定和保证系统的稳定性。因此，理论上该方法可以推广到任意的力觉交互系统(HIS)。但目前的实验结果还局限于简单的虚拟环境，如虚拟墙或对力觉逼真度无精度要求的简单几何形体。对于复杂虚拟环境与3自由度以上的力觉交互设备组成的力觉交互系统(HIS)，尚未看到关于稳定性的实验数据和分析结果。

现有稳定性研究所基于的简化假设，与应用系统的实际情况相差较大，用于解决实际问题时，还需要进一步针对具体对象的复杂情况，探讨切实可行的控制算法。以牙科手术仿真(Dental Surgery Simulation)为例，这些复杂情况包括：

(1) 牙齿和手术工具是采用三角网格或三维实体离散表达的具有复杂形状的模型，而非解析方程表达的连续模型；

(2) 牙齿切削时要发生材料去除，虚拟环境模型随时间变化；

(3) 牙齿与工具的接触交互是空间多自由度非线性动力学系统。

根据对简化系统所进行的研究，虚拟刚度与伺服频率影响系统稳定性，虚拟刚度不能超过交互设备阻尼所允许的稳定范围，当伺服频率增加时，允许刚度的上限可以提高[13]。这些结果对实现牙科手术模拟这样的复杂应用系统有借鉴作用。

本研究团队在模拟牙面探查时，发现用虚拟工具接触牙齿表面时，若刚度较大，则会导致设备振动。类似地，在牙体预备模拟中，发现用虚拟工具切削牙齿时，大刚度也导致设备振动。以上两种情形，减小刚度都可以减小或消除振荡。但随之而来的问题是由于接触力过小，系统丧失了逼真度[14]。因此，解决复杂力觉交互系统(HIS)的稳定问题，是提高系统逼真度的迫切需要。

力觉交互设备失稳是导致力觉仿真系统失真的重要因素之一。因此，发现失稳机理(mechanism of unstable behaviour)，获知系统的稳定条件和稳定控制方法，对于逼真地实现力觉交互具有重要意义。

在稳定性研究中，对失稳机理没有给出明确的物理意义解释。Colgate[13]等学者从z判据出发，推导出系统被动性充要条件的数学描述，没有对力觉交互过程中失稳的原因给出直观的解释。Gillespie[15]建立了人的可重复运动动力学显式模型，并将这个模型作为力觉系统传递函数的一个环节，指出“能量泄漏”是导致虚拟墙壁模拟时产生振动的原因。但该研究只针对单边约束的虚拟墙壁，没有考虑复杂虚拟环境下的失稳机理，不够全面。缺乏明确的解释，对于虚拟环境设计者和力觉交互设备设计者来说，就意味着不能获得设计过程的感性认识。鉴此，本研究团队基于稳定合成算法的研究现状，探索非解析表达复杂虚拟环境下，基于阻抗显示设备的力觉交互系统稳定性丧失的物理机理。

当系统丧失稳定性时，需要施加适当的渲染或控制，以保证系统稳定性，消除交互设备的振动。目前，消除力觉设备振动的方法主要包括虚拟匹配方法(Virtual Coupling Method，VCM)[16]和时间域被动性控制方法(Time-Domain Passivity Control，TDPC)[7]等两种。

虚拟匹配方法(VCM)的基本原理是对进入虚拟环境的运动信号和虚拟环境输出的力信号同时进行处理，使最终信号关系满足双端口网络无条件稳定的范围。该方法在具体实现时存在以下3个方面的局限：

第一，虚拟匹配方法(VCM)的前提要求操作者和虚拟环境都是被动，设计虚拟匹配单元，保证力觉设备和虚拟匹配单元组成的双端口网络被动，在切削仿真系统中，由于发生材料去除，虚拟环境为动态时变，被动性未必能够保证；

第二，虚拟匹配方法(VCM)一般应用于固定刚度的环境中，通过实验可以得到一个合适的匹配系数，但对于切削仿真这类非线性虚拟环境，如何选择匹配系数，是有待研究的问题；

第三，在基于三角片模型的交互算法中，如何引入虚拟匹配算子是未知问题。

虚拟匹配单元的具体实现形式表现为由弹簧和阻尼元素串并联构成信号处理环节。对解析形式表示的一维虚拟墙壁，可以推导出解析信号处理计算表达式，但对于采用三角片模型描述的物体，计算算法比较复杂。罗杨宇[17]针对一维虚拟环境，给出了基于波变量的虚拟匹配方法，但对于三维复杂虚拟环境，这种方法难以推广。

时间域被动性控制方法(TDPC)基于被动性假设，将操作者、力觉交互设备、虚拟环境分别看作电网络端口环节，定义能量观测器来描述一个端口元件被动性损失的程度，在被动性损失时，对力信号进行修正，达到保证整个系统被动性的目的。这种方法在计算能量时需要进行速度微分，在低速操作时会引入比较大的计算噪声，造成力觉设备的振动和噪声。此外，采用该方法针对一个大刚度(超过Phantom Desktop刚度阈值)虚拟墙壁进行接触交互试验，仍然存在振动现象，说明该方法有待改进。

基于力觉合成算法的研究现状，本文目的在于报告本研究团队以开发高性能牙科手术模拟训练系统为目标，针对非解析表达复杂虚拟环境下，基于阻抗显示设备的力觉交互系统(HIS)的系统稳定性研究的系统理论成果。

2 交互设备的稳定性

【定义1设备稳定】 指在模拟给定力觉交互任务时，交互设备不产生振动。

【约定1研究前提】 在讨论设备稳定性时，假设操作者是被动的，并用虚拟墙(Virtual Wall)模型代表虚拟环境，用设备可稳定模拟该虚拟墙的最大刚度表示设备的最大可模拟虚拟刚度。

2.1 提高稳定性的控制方法

通过改变系统的物理参数[18-19]和控制策略[7-8,20-22]可以有效的提高力觉交互系统(HIS)的稳定性。本研究团队采用电流闭环控制策略(Current Closed Loop Control)[23]和多更新率控制策略(Multirate Control)[24]等两种方法提高系统稳定性。

2.1.1 电流闭环控制

基于开环阻抗控制策略的系统控制结构见图3。

T为系统采样周期；1/z为上位机的计算延时；ZOHT为零阶保持器；为设备末端的速度；X为设备末端位置；XT为采样位置；Factive为操作者施加的主动力；Fhp为操作者施加的被动力；Fh为操作者施加给设备的合力；Fe为虚拟力；Fd为施加在设备末端的合外力。

[假设1] 操作者是被动的，其阻抗(operator passive impedance)采用质量-阻尼-弹簧模型(mass-damper-spring model)[25]。

(1)

式中，H(s)为操作者的等效被动阻抗；mh为操作者等效质量；bh为操作者等效阻尼；kh为操作者等效刚度。

[假设2] 交互设备阻抗(device impedance)采用质量-阻尼模型(mass-damper model)。

D(s)=mds+bd

(2)

式中，D(s)为交互设备等效阻抗；md为交互设备等效质量；bd为交互设备等效阻尼。

[假设3] 虚拟环境阻抗(virtual environment impedance)采用弹簧模型(spring model)。

(3)

式中，E(z)为虚拟环境阻抗；ke为虚拟环境刚度。

则系统传递函数

(4)

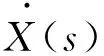
由此，可以得到系统的稳定性条件

(5)

从式(5)可以看出，开环阻抗控制下，设备的最大可模拟虚拟刚度与交互设备自身的阻尼bd和操作者的阻尼bh成正比，与系统的采样周期成反比。

电流闭环控制策略是指在电机回路增加电流传感器，测量电机的实际电流，构成电流反馈；进而计算电机实际输出力矩，得到设备末端的实际输出力

Fm=J-1KτI
Kτ=diag{kτ1，kτ2，…，kτn}

(6)

式中，Fm为设备末端的实际输出力；Kτ为设备的电机扭矩常数矩阵；J为设备末端笛卡尔空间到驱动电机关节空间的速度雅克比矩阵；I为驱动电机电流构成的向量。

电流闭环控制策略对应的系统控制结构见图4。其中，交互设备阻抗模型和操作者阻抗模型与图3相同。ZOHT2是T2采样周期下的零阶保持器，一阶低通滤波器F(z2)用于对电流信号滤波，消除其中的高频噪音。G(z2)为PID控制器，用于减小设备末端实际输出力与期望输出力之间的误差。设备期望输出的虚拟力Fe和滤波后设备末端的实际输出力之差是PID控制器的输入，其输出和期望虚拟力的和作为控制信号，控制电机的输出力矩。

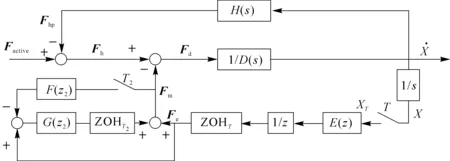
图4 电流闭环策略的离散系统控制结构

由于电流闭环控制器的伺服频率远远高于1 kHz的力伺服频率，因此滤波器和PID控制器部分可以看成连续系统(见图5)。

图5 电流闭环策略的连续系统控制结构

设备末端的实际输出力与期望输出虚拟力之间存在如下关系

(7)

设F(s)为一阶低通滤波器的传递函数，G(s)为PID控制器的传递函数，则

(8)

式中，τ为滤波器时间常数。

(9)

式中，kp为PID控制器的比率系数；ki为PID控制器的积分系数；kd为PID控制的微分系数。

将式(8)和式(9)代入式(7)可得

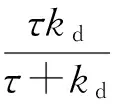
(10)

(11)

(12)

从式(10)可以看出，为了保证系统的逼真性，即在电流闭环控制策略下，使操作者感受到的虚拟环境的刚度保持不变，必有coef=1,于是

kp=kd/τ

(13)

取ki=0，则g1(s)=0(见式(12))，式(10)变为

(14)

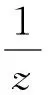
(15)

式中，SAMPLE(z)为系统采样器的等效传递函数。

将式(15)代入式(14)，得到

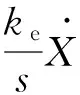
(16)

则操作者施加的主动力

(17)

因此，电流闭环系统的传递函数

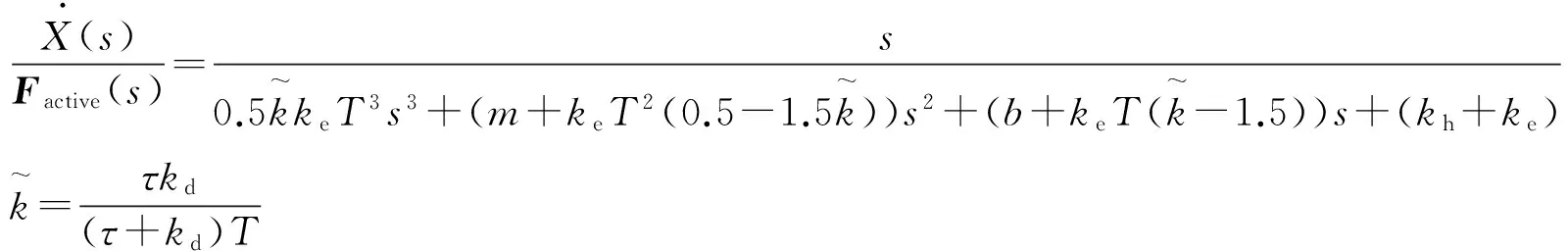
(18)

式中，m为系统等效质量；b为系统等效阻尼。

所以电流闭环系统的稳定性条件

(19)

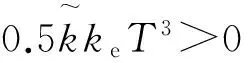
(20)

(21)

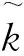
(22)

式(20)和式(21)成立的充分必要条件是

(23)

系统采样周期T=10-3s，而系统的等效阻尼b和等效质量m数值上是同一个量级，因此bT≪m。所以

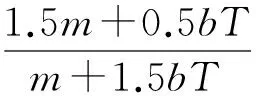
(24)

式(22)成立的充分必要条件是

(25)

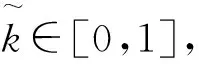
(26)

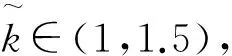
(27)

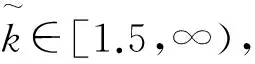
(28)

电流闭环控制策略对提高稳定性的效果可以通过实验方法进行验证。以3自由度(3DOF)力觉交互设备为实验平台，见图6(a)。系统坐标系定义和设备的机构简图见图6(b)。将设备的轴2和轴3固定，只允许轴1运动，转角范围是θ1∈[30°,150°]。设备末端P点的位置分辨率是0.05 mm；受电流传感器量程限制，设备末端P点的最大输出力是2.5 N。虚拟环境采用1自由度弹簧模型，见图6(c)，则虚拟力

(29)

虚拟环境渲染和力觉合成在上位机PC进行，电流闭环控制策略在下位机DSP控制器进行，下位机通过USB2.0与上位机通信。力觉渲染的伺服频率是1 kHz，电流闭环的伺服频率是20 kHz。

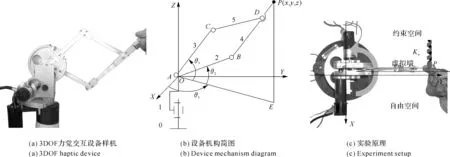
图6 3DOF力觉交互设备和实验原理

采用开环控制策略时，当虚拟墙刚度超过2.8 N/mm，操作者会明显感受到设备的振动。图7给出了虚拟墙刚度为2.8 N/mm和3.0 N/mm时，设备末端的位置和速度曲线。从图7可以看出，当虚拟墙刚度为2.8 N/mm时，设备末端的位置和速度曲线没有出现震荡，表明设备没有出现振动,设备稳定；当虚拟墙刚度达到3.0 N/mm时，设备末端的位置和速度曲线出现剧烈震荡，设备末端出现了明显的振动，此时设备不稳定。因此开环控制策略下，设备可模拟的最大虚拟刚度约为2.8 N/mm。

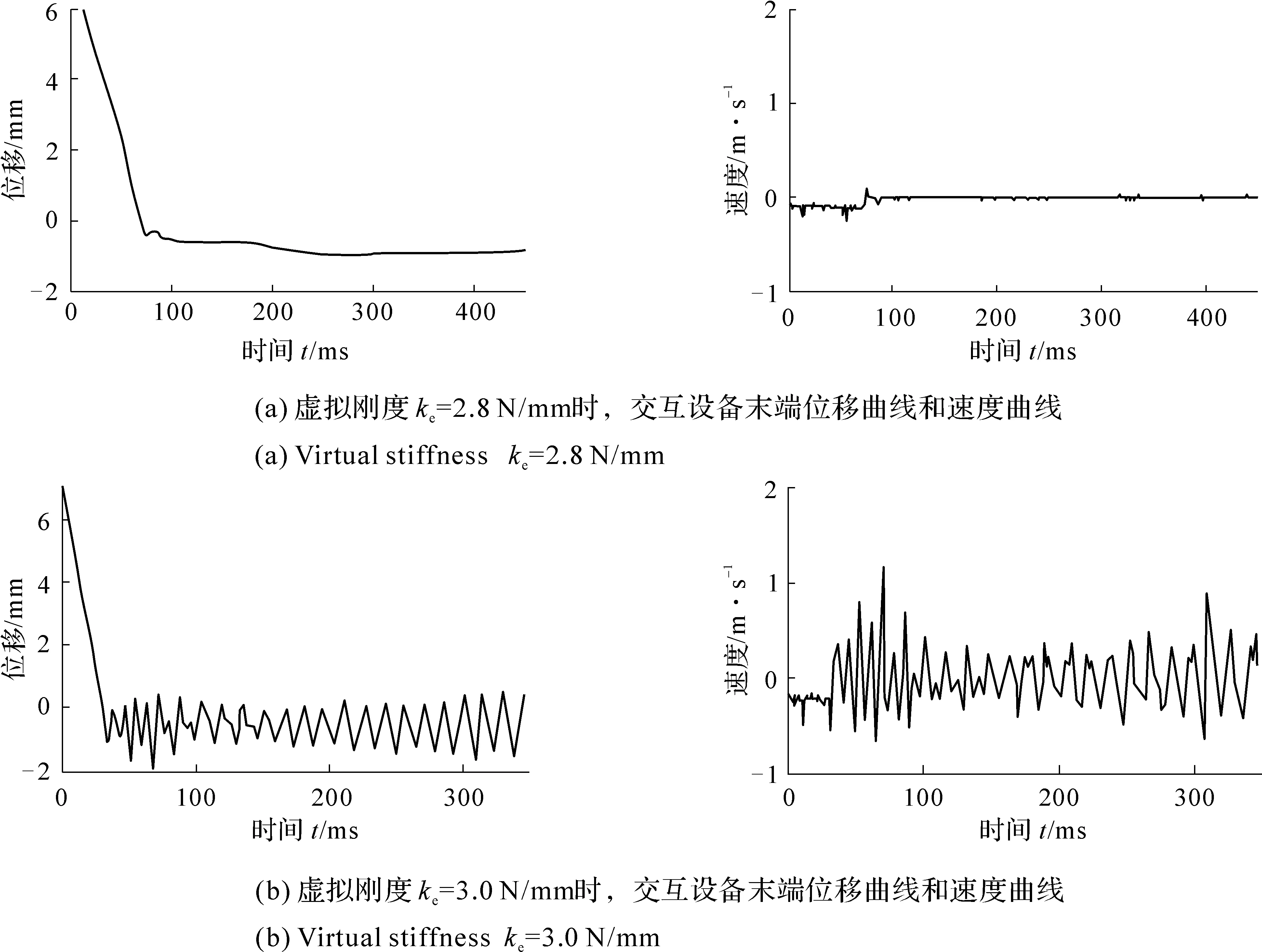
图7 开环控制下，虚拟墙实验中不同刚度条件下，设备末端位移、速度曲线

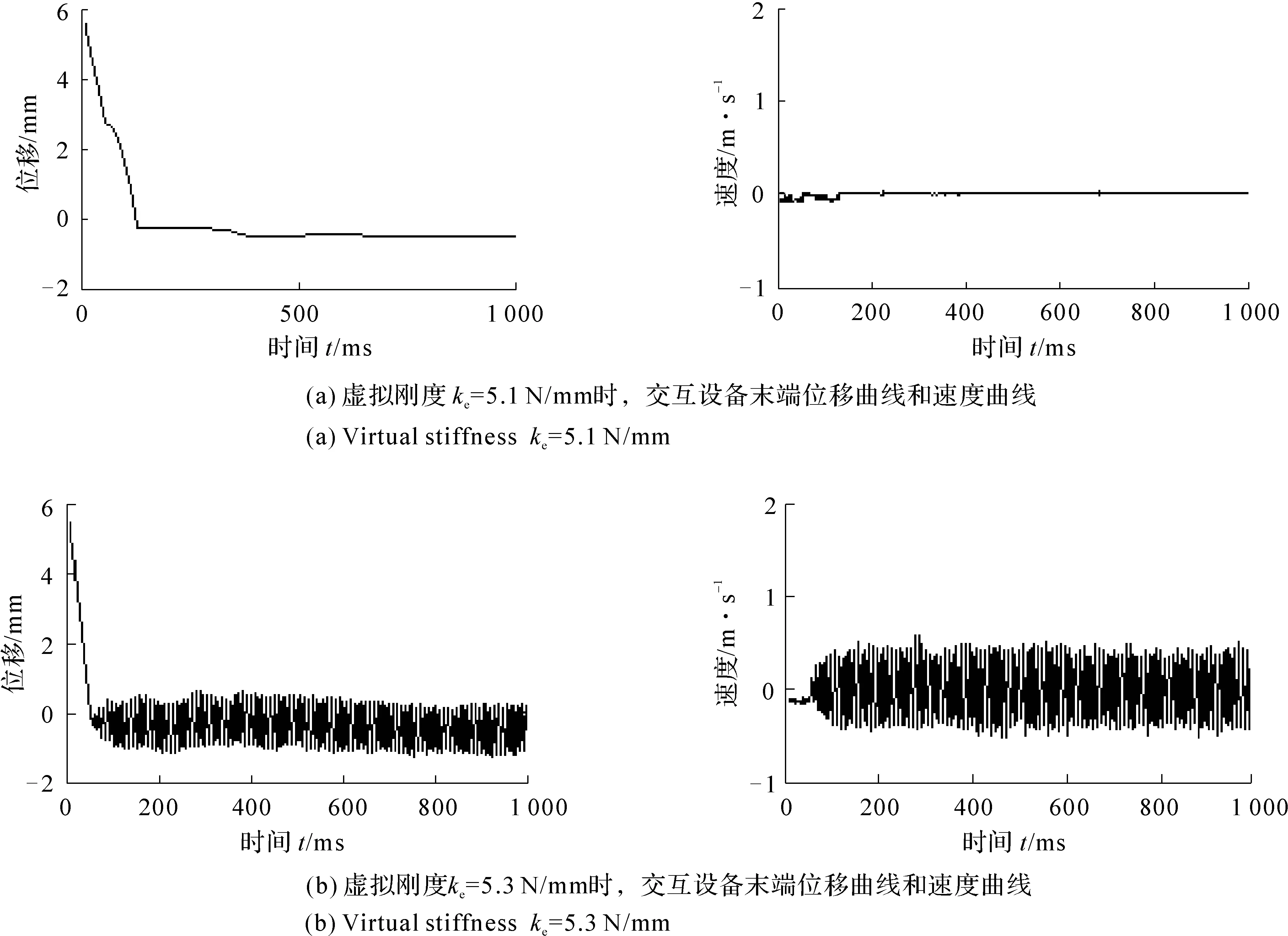
图8 电流闭环控制下,虚拟墙实验中不同刚度条件下，设备末端的位移、速度曲线

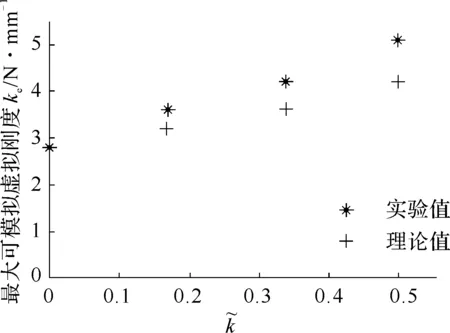
图9 不同条件下，实验和理论分析最大可模拟虚拟刚度对比

2.1.2 多更新率控制

从系统稳定性条件(见式(5))可以看出，减小系统采样周期，提高系统更新频率，可以有效地增加系统可模拟刚度。但上位机的力觉合成(haptic rendering)更新频率受多种因素制约，包括虚拟场景建模、虚拟物体碰撞检测和力觉合成算法的复杂度。因此，本研究团队提出了一种多更新率控制策略(multirate control)，在不增加上位机更新频率的前提下，在下位机微控制器上实现更高频率的插补运算。例如，下位机以10 kHz或者更高的频率对设备末端的位置采样，同时对设备末端的输出力进行预估计算(见图10)。

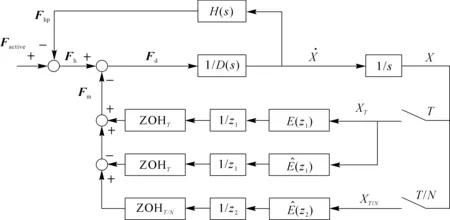
T为来自上位机(PC)的虚拟力更新周期；T/N为下位机控制器控制电机力矩信号的更新周期；N为下位机更新频率相对上位机更新频率的倍数；为虚拟环境在采样周期为T时的阻抗模型；为虚拟环境在采样周期为T/N时的阻抗模型；1/z1为采样周期为T时的计算延时；ZOHT为采样周期为T时的零阶保持器；1/z2为采样周期为T/N时的计算延时；ZOHT/N为采样周期为T/N时的零阶保持器，XT/N是采样周期为T/N时采样的设备末端位置。

控制器利用当前插补时刻的设备位姿，实时计算虚拟力增量，从而实现在两个连续上位机虚拟力的间隔内的高频率插补。当虚拟环境是虚拟墙模型时，多更新率插补策略见图11。

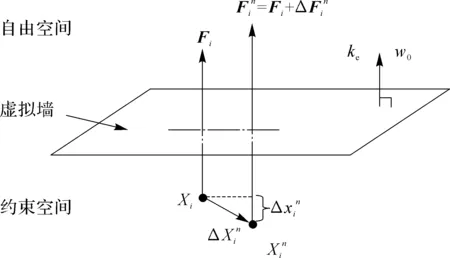
ke为虚拟墙的刚度；w0为虚拟墙的法向量；Fi为在采样时刻ti时设备末端的虚拟力；为插补时刻时的设备末端的虚拟力；Δ为插补时刻时设备末端的虚拟力的增量；Xi为在采样时刻ti时设备末端的位姿；为插补时刻时设备末端位姿；Δ为在插补时刻=ti+n×T/N时设备末端的位姿增量；Δ为位姿增量Δ在虚拟墙的法向量w0上的投影。

多更新率插补算法如下。

(30)

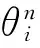
多更新率控制(见图10)时的系统传递函数

(31)

因为2N(mh+md)+keT2>0，2Nkh+ke>0恒成立，因此系统稳定的充分必要条件是

2N(bh+bd)-(2N+1)keT>0

(32)

由式(32)可以得到，多更新率控制时的系统稳定性条件

(33)

比较式(33)与式(5)可以看出，当N=1时，系统的稳定性条件和单更新率控制时的系统的稳定性条件相同；增大N可以增大系统可模拟虚拟刚度，提高系统的稳定性，但最大增大幅度为1.5倍。

2.2 交互设备最大可模拟虚拟刚度分布

交互设备的稳定性可以用设备最大可模拟虚拟刚度度量[26]。文献[10,27-29]的研究表明，设备阻尼、控制系统采样周期、设备位置分辨率，库伦摩擦，以及操作者和设备输出力之间的不平衡性都会影响系统的稳定性。文献[30]提出，在两个连续采样时间，电机输出力矩的较大跳变和操作者与电机输出力带宽的差异性是导致系统失稳的两个主要因素。另外，交互速度(Interaction Velocity)——即设备与虚拟墙接触时的速度同样会影响系统的稳定性。例如，当交互设备与同样刚度的虚拟墙在同一点接触时，较慢的交互速度可以达到较好的稳定性，而较快的交互速度则更容易破坏系统的稳定性，使设备出现振动。为解释其原因，本研究团队提出以下假设。

[假设4] 交互设备出现振动的原因是在两个连续采样时刻，电机输出力矩的阶跃值超过了某个特定的阈值。

根据“假设4”，保证系统稳定的条件是

∀i,Δτi≤Δτthresh

(34)

式中，Δτi是在相邻两个采样时刻电机力矩的增量；Δτthresh是保证系统稳定的阈值，这个稳定阈值受电机自身性能、设备阻尼，以及操作者施加与设备的主动力有关。

若交互设备库伦摩擦可以忽略，关节阻尼不变，且操作者在交互过程中的抓持力不变，多自由度的力觉交互系统(HIS)稳定性条件可以进行如下考察。

考虑两自由度情况，假设力觉交互设备驱动电机关节空间的刚度矩阵[31]

Ko=JTKxJ

(35)

式中，J为设备末端笛卡尔空间到驱动电机关节空间的速度雅克比矩阵；Kx为设备末端笛卡尔空间的虚拟刚度矩阵。

设，在两个相邻采样时刻，Δθ为电机转角增量，Δτ为电机力矩增量，则

Δτ=KoΔθ

(36)

设，WW′是刚度为ke的虚拟墙，在坐标系O′-X′Y′下(见图12)虚拟墙刚度矩阵

(37)

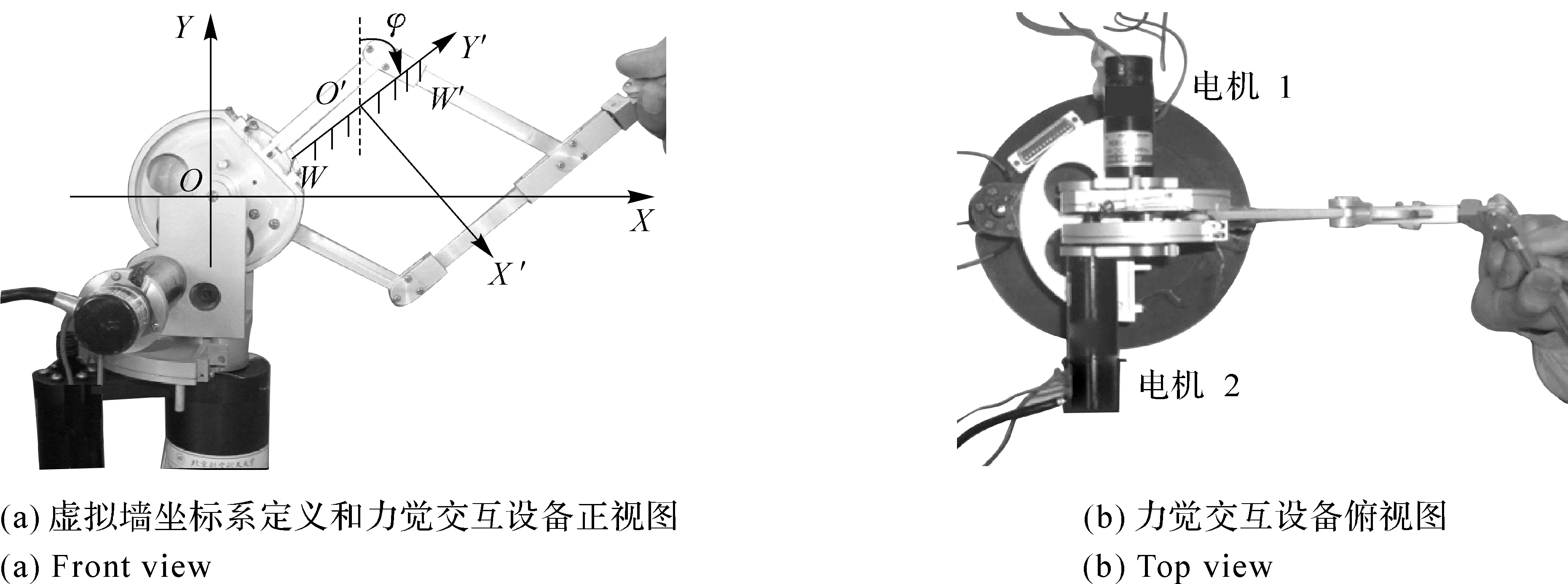
图12 虚拟墙坐标系定义和力觉交互设备

在坐标系O-XY下，虚拟墙的刚度矩阵为Kx，则

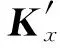
(38)

式中，φ为从坐标系O′-X′Y′到坐标系O-XY的旋转角，R为变换矩阵。

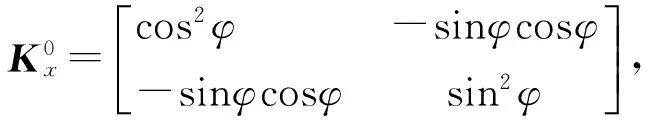
(39)

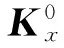
将式(35)和式(39)代入式(36)，可得

(40)

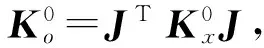
(41)

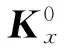
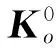
Δθ=a1v+a2v′a1∈R,a2∈R

(42)

将式(42)代入式(41)，可得

Δτ=b1kλv

(43)

为了叙述简便，令‖Δθ‖=1。由于‖v‖=‖v′‖=1,所以|a1|≤1,|a2|≤1，因此

(44)

(45)

则式(43)可以重新写为

(46)

为了保证系统稳定，每个电机的力矩跳变都不能超过其各自的阈值。反之，如果任一个电机的力矩跳变超过了其阈值，系统将会失稳。假设两个电机的力矩跳变阈值相同：

如果|v1|>|v2|，则电机1的力矩跳变大于电机2，电机1更容易失稳振动，此时可模拟的最大虚拟刚度由电机1决定；

如果|v1|<|v2|，则电机1的力矩跳变小于电机2，电机2更容易失稳振动，此时可模拟的最大虚拟刚度由电机2决定。

对给定的力觉交互设备，每一个电机力矩的跳变阈值可以用以下实验方法进行测量。

设力觉交互设备为2DOF设备，其操作末端的位置映射为虚拟环境中的A点(见图13中绿色小球)。

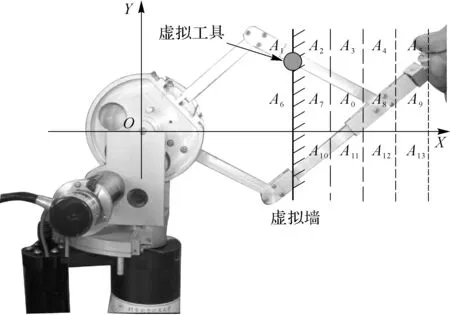
图13 平行于Y轴的虚拟墙

由于交互速度会对系统的稳定性产生影响，因此尽量保证每次实验的交互速度相同。当交互设备在Ai点接触虚拟墙时，按一定步长不断增大虚拟墙刚度，直到操作者感觉到设备振动，这样得到在每一个测试点，设备可模拟的最大虚拟刚度。在第一组实验中，虚拟墙平行于Y轴，测试点依次位于设备工作空间内的A0,A1,…,A13点。设备在每个测试点可模拟的最大虚拟刚度见图14。测量结果显示在设备工作空间内，最大可模拟虚拟刚度在不同位置点存在很大的差异。

X轴和Y轴分别表示测试点的X坐标和Y坐标，Z轴表示该点的最大可模拟虚拟刚度。

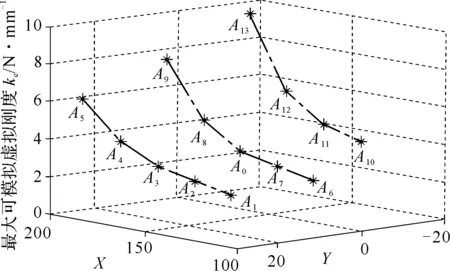
在同一个测试点，改变虚拟墙的方向进行类似的测量实验，可以得到在该点不同方向上的最大可模拟虚拟刚度。设备在A0点，依次测量虚拟墙W1,W2,W3,W4的最大可模拟刚度(见图15)。虚拟墙W1,W2,W3,W4对应的虚拟墙的旋转角φ分别为0°，45°，90°，135°。最大可模拟虚拟刚度与虚拟墙旋转角之间的关系见图16。从图16可以看到，即使在同一个测试点，不同方向虚拟墙的最大可模拟刚度同样存在很大差异。

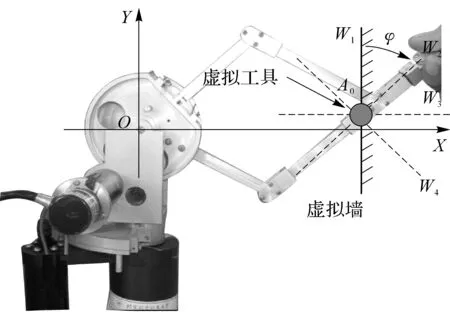
图15 A0点不同方向的虚拟墙

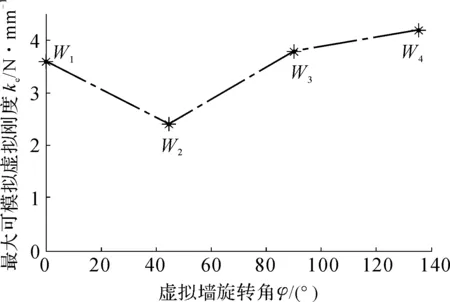
图16 A0点不同方向的最大可模拟虚拟刚度测量结果

从图14和图16可以看出，交互设备的最大可模拟虚拟刚度不仅与设备末端的位置有关，还与虚拟墙方向即虚拟力方向有关，并且最大可模拟虚拟刚度随位置变化和虚拟力方向变化而剧烈变化。因此，对一个给定的力觉交互任务，为了保证整个交互过程中，设备都稳定，必须求解设备在任务空间内的最大可模拟虚拟刚度的分布，充分了解设备在任务空间内的性能。

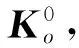
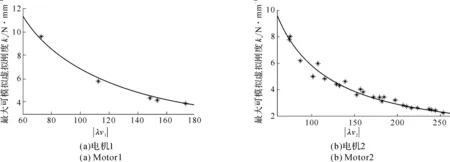
图17 电机失稳曲线

图17中“*”点表示实验结果，曲线表示拟合结果，拟合的曲线方程分别是ke=603/|λv1|和ke=575/|λv2|。该拟合曲线表明最大可模拟虚拟刚度ke与|λvi|成反比，与式(46)的结论吻合。由此得到电机1的力矩跳变阈值为603 N·mm和电机2的力矩跳变阈值为575 N·mm。电机1和电机2的力矩跳变阈值相差约4.6%，二者比较接近。这里拟合得到的两个电机的力矩跳变阈值是基于关节电机转角增量的模为1的条件得到的，是一个分析的结果，并不是设备电机的实际跳变阈值。

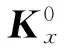
(47)

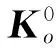
(48)

类似地，在每一个位置采样点，都可以计算得到设备的最大可模拟虚拟刚度(见图18(b))。其中，X轴表示设备末端的位置，用夹角α表示；Y轴是对应的最大可模拟虚拟刚度。从图18(b)可以看出，在虚拟圆上各点，设备可模拟的最大虚拟刚度在2.3 N/mm与5.2 N/mm之间变化。为了保证在虚拟圆上任意点进行接触交互时，设备均稳定，虚拟圆的刚度必须小于2.3 N/mm。图19显示了当虚拟圆刚度是2.6 N/mm和2.0 N/mm时，设备末端的虚拟力和末端位置的关系。从图19(a)可以看到，当虚拟圆刚度是2.6 N/mm时，在150°和330°附近设备出现了明显的振动。从图18(b)也可以看出，在虚拟圆上的150°和330°附近，设备可模拟的最大虚拟刚度只有2.3 N/mm，小于模拟的虚拟刚度，因此设备出现振动失稳；而在其他位置，设备可模拟的最大虚拟刚度大于2.6 N/mm，设备不会失稳出现振动。当虚拟刚度减小到2.0 N/mm时，振动消失，在虚拟圆上任意点进行交互，设备都稳定。

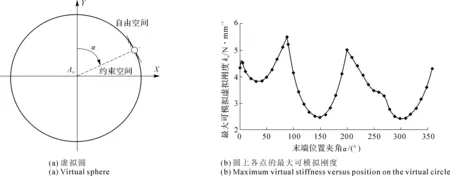
图18 虚拟圆和圆上各点的最大可模拟虚拟刚度

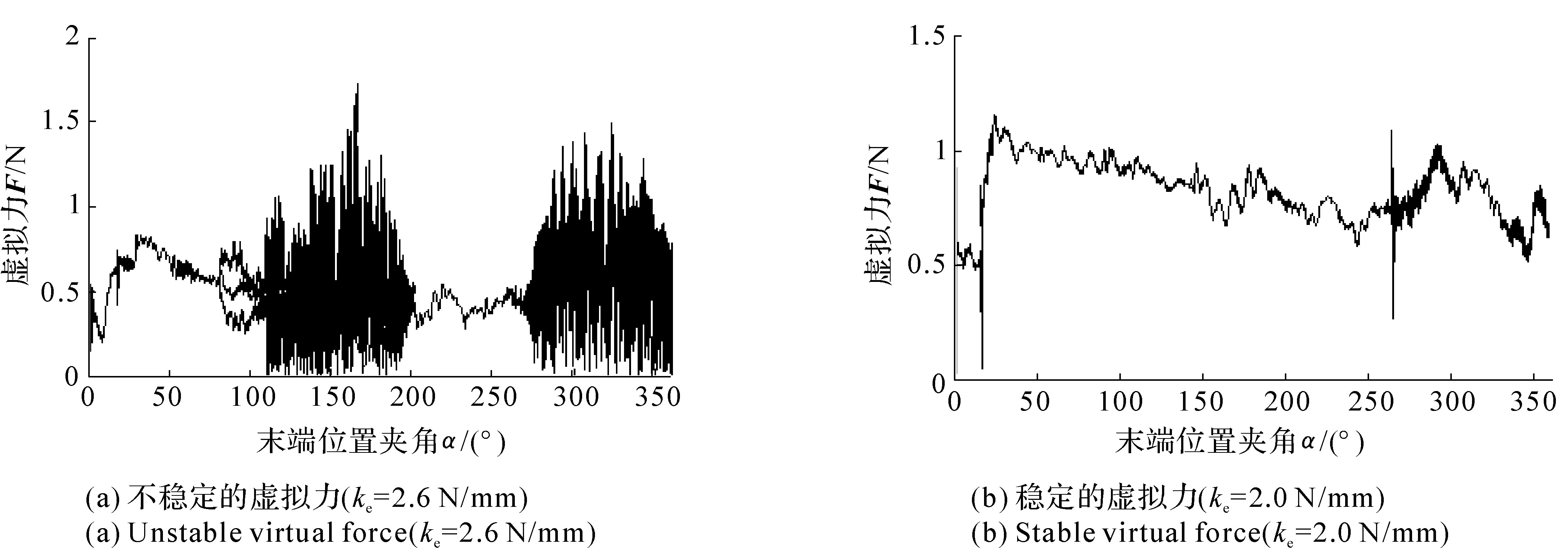
图19 不同虚拟刚度条件下，虚拟圆上各点的虚拟力

3 力觉合成的稳定性

针对阻抗再现(impedance display)的力觉交互设备，在力觉合成算法中，存在物理工具(haptic tool)和图形工具(graphic tool)等两类虚拟工具。物理工具代表力觉反馈设备在虚拟环境中的化身，始终与力觉反馈设备末端手柄的运动保持同步；图形工具代表计算机屏幕上显示的虚拟工具。

在模拟自由空间的操作任务时，物理工具和图形工具位置和姿态保持重合；在模拟约束空间的操作任务时，当虚拟工具和被操作物体接触后，物理工具会嵌入被操作物体边界内部，图形工具被约束在物体的表面上静止或在接触状态下保持相对运动。因此，力觉合成稳定性(Stability of Haptic Rendering)的内涵包括两个方面：

【内涵1图形工具的稳定性】 针对阻抗再现的虚拟环境，当人抓持力觉设备运动时，物理工具的运动是一个空间连续的信号，在出现接触状态变化时(包括从自由空间进入约束空间，或工具在物体表面的不同几何细节上滑动时)，图形工具不应该出现位置和姿态的突变，如果出现突变，则认为丧失稳定性。

【内涵2力和力矩的稳定性】 当操作者抓持力觉设备运动时，物理工具的运动是一个空间连续的信号，在出现接触状态变化时，力和力矩也应该是一个连续变化的信号，否则力觉设备会出现振动、噪声等现象，即认为丧失稳定性。

针对力觉合成稳定性问题，笔者提出力觉合成算法稳定性分析思路(见图20)。

图20 力觉合成算法稳定性分析思路

【step1】 进行失稳机理分析，找出虚拟环境丧失稳定性的原因；

【step2】 提出保证力觉合成稳定性的处理算法；

【step3】 针对口腔检查、龋坏诊断、牙体预备等典型操作的算法稳定性，进行试验验证。

3.1 失稳机理分析

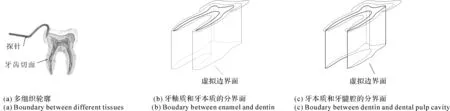
当两个刚体接触交互时，接触点处会形成不可穿越的单边约束(Uni-Lateral Constraint)。当一个刚体工具相对于一个刚性物体保持接触并产生相对滑动或转动时，接触点的位置将在物体表面上变化。针对牙科手术模拟的非线性虚拟环境力觉模拟任务，文献[30]提出了动态单边约束(Dynamic Uni-Lateral Constraint，DUC)的概念——将牙齿表面的接触过程描述为位置和方向瞬时变化的刚性虚拟墙，从而将复杂虚拟环境的稳定性转换为动态虚拟墙(Dynamic Virtual Wall)的稳定性，再进行分析(见图21)。

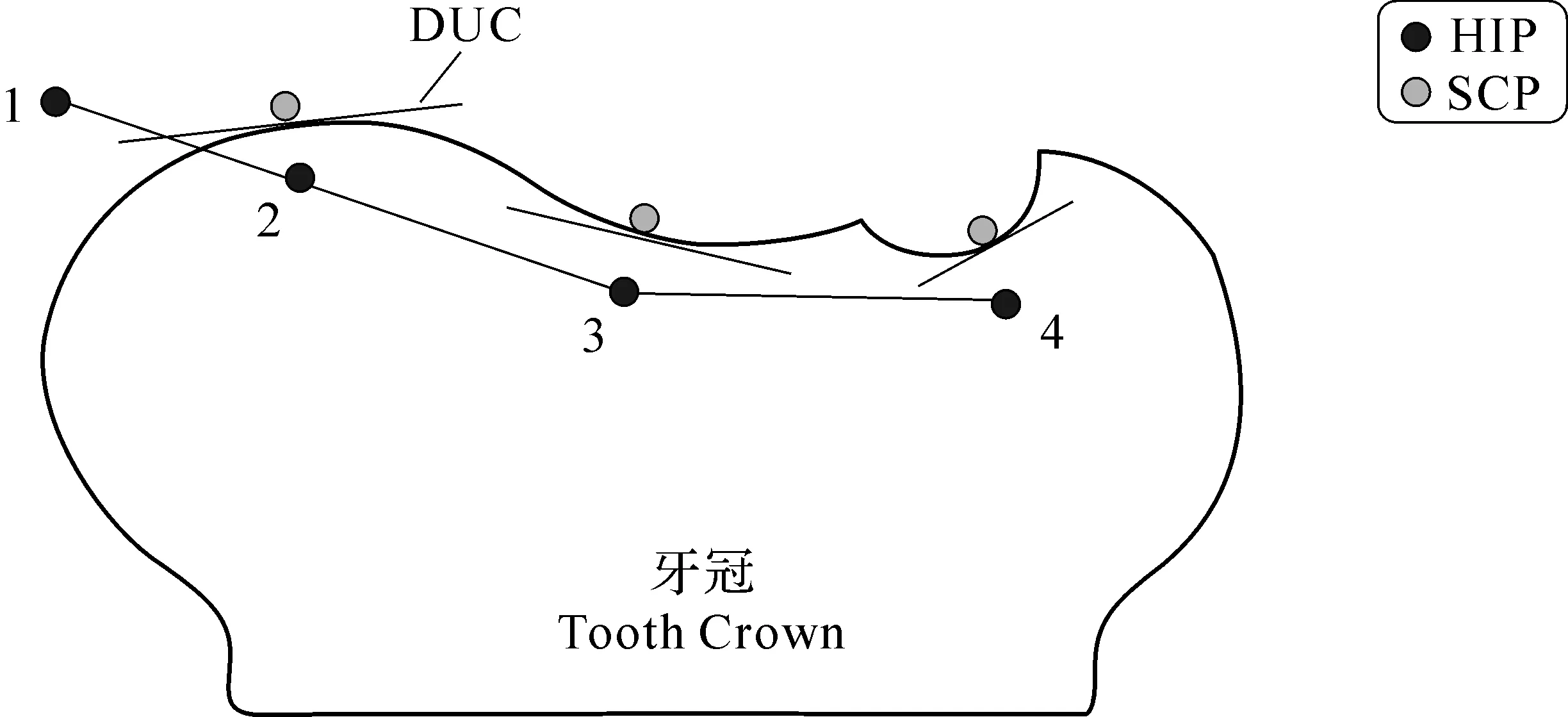
图21 复杂虚拟环境的动态单边约束演化

在图21中，交互工具简化为一个点，HIP(Haptic Interface Point)代表物理工具(haptic tool)，SCP(Surface Contact Point)代表图形工具(graphic tool)。点1～点4连线代表HIP在相邻4个仿真循环中的运动轨迹，3条切线代表每个时刻图形工具与牙齿表面接触点的局部近似形状，即局部的动态单边约束(DUC)。

动态虚拟墙的稳定性包括两层含义：

(1) 当虚拟墙的位置和方向固定时，工具和虚拟墙之间的接触刚度应该小于力觉反馈设备可模拟的刚度上限，否则交互过程将失稳；

(2) 在虚拟墙的位置和方向变化的瞬间，应保证计算得到的虚拟力信号不出现过大阶跃，即保证工具和虚拟墙之间的等效接触刚度小于力觉反馈设备可模拟刚度的上限，否则交互过程将失稳。

以力觉交互装置和一维虚拟墙接触交互为对象，进行了失稳机理分析。设虚拟墙法线为x轴反方向，边界为x=0，x<0的区域为自由空间。图22中给出了当物理工具的位置在虚拟墙两侧变化时，交互装置位置(Xd)、作用在交互装置手柄上的合力(F)、交互装置移动速度(Vd)的对应变化过程示意，其中合力(F)包括人手施加的主动力和电机输出的被动力。

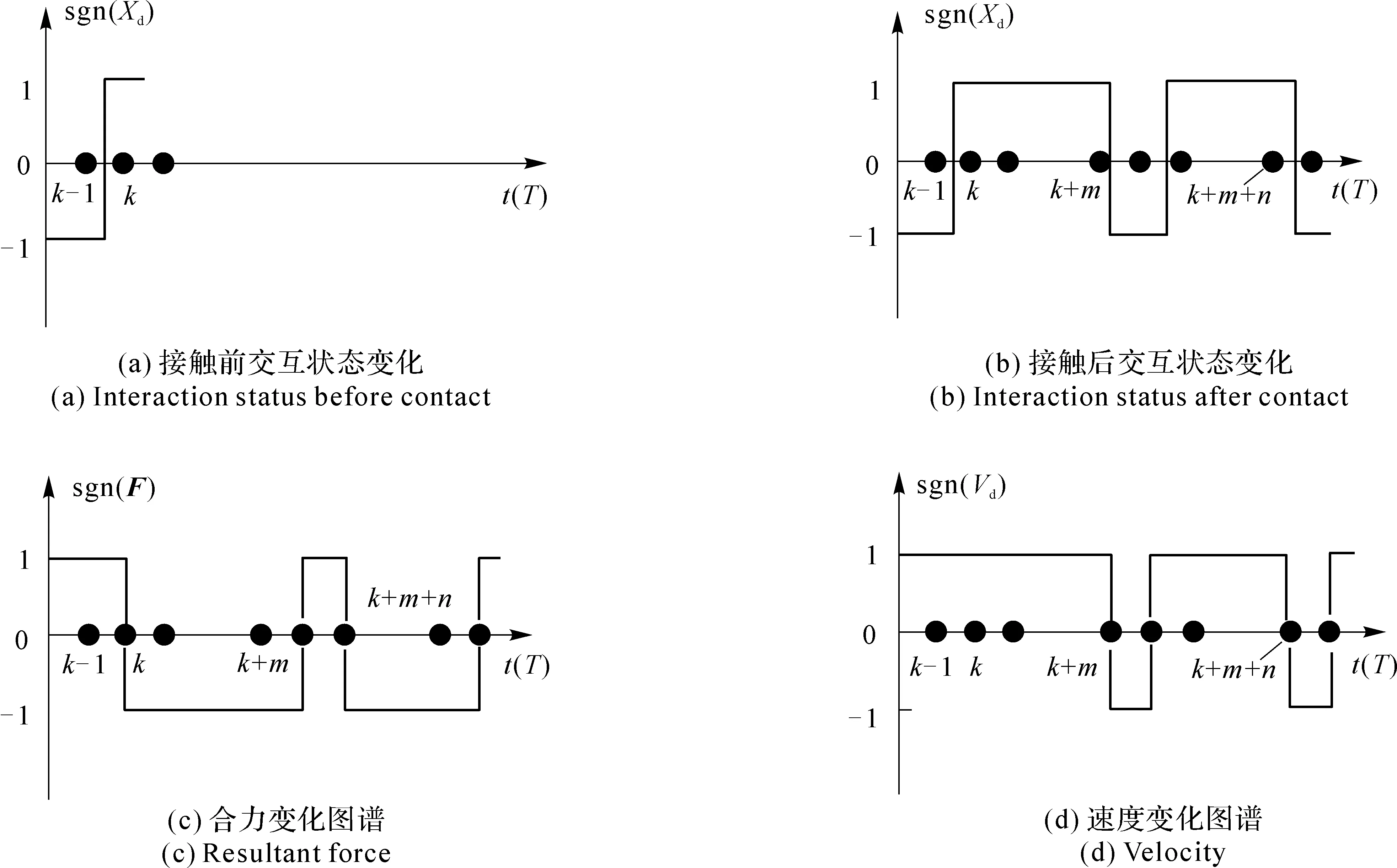
图22 单边约束交互时的信号变化图谱

图22(a)表示在k-1时刻及以前，物理工具处于自由空间，在k-1时刻及k时刻之间的某个时刻，物理工具穿过了虚拟墙边界进入到约束空间。图22(b)表示在k+m时刻之后，物理工具由约束空间进入到自由空间，然后在两个采样周期后又再次进入到约束空间。图22(c)表示在上述物理工具运动轨迹下相对应的合力变化规律，可以看到在k时刻之前，交互装置只受到人手的主动力，合力方向沿x轴正方向，在k时刻之后，交互装置同时受到人手的主动力和电机输出的被动力。当虚拟墙的刚度设置为一个较大值时，将导致电机输出的被动力大于人手的主动力，因此合力方向沿x轴反方向，直到k+m时刻之后，物理工具回到自由空间，电机输出为0，而人的输出力仍然保持，因此合力方向再次恢复为沿x轴正方向。由于上述合力的方向变化，将导致出现图22(d)表示的交互装置移动速度的变化规律，即出现交互装置的振动。

通过分析合力变化的上述规律，得到力觉交互算法失稳的两个原因：

【原因1】 当交互状态在一个动态单边约束内部变化，或在两个动态单边约束之间变化时，虚拟力信号的变化值超过了允许的阈值；

【原因2】 人的输出力带宽小于设备的输出力带宽，导致人的主动力和电机输出力不平衡。

当上述两个原因同时存在时，力觉交互系统(HIS)将丧失稳定性。

3.2 保持稳定性的力觉合成算法

力觉合成算法既要保证逼真度和实时性要求，又需要保证计算稳定性。此外，对不同操作任务(例如牙科手术中牙齿表面探查和牙齿切削)，其计算量存在差异。因此，本研究团队提出基于多更新率的力觉合成计算架构(见图23)，以满足计算逼真度和计算实时性之间的矛盾折衷。

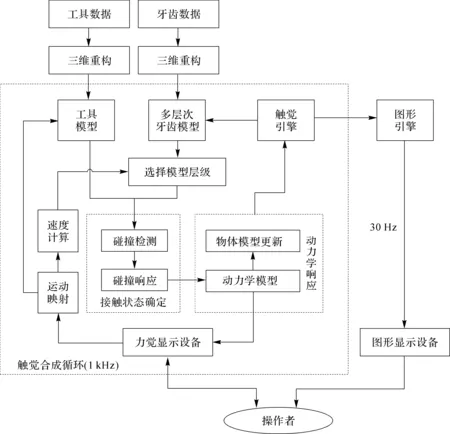
图23 力觉合成技术的计算架构[15]

图23中，离线模块包括虚拟环境建模(牙齿模型和工具模型)，在线模块包括1 kHz的触觉合成循环和30 Hz的图形显示循环。在每个触觉合成循环中，由触觉引擎负责时间调度，主要计算模块包括，力觉显示设备的位姿测量、物理空间到虚拟空间的运动映射、交互速度计算、速度驱动的模型层级选择、基于均匀空间划分和时间连续性的实时碰撞检测算法、基于虚拟代理的接触碰撞响应算法、交互力计算的动力学模型、物体更新方法等[14]。

基于对失稳机理的分析，本研究团队提出了提高系统稳定性的限制参量。

【限制参量1复杂虚拟环境中的等效接触刚度(EquivalentContactStiffness，ECS】 相邻两个仿真时刻下，计算得到的虚拟力信号变化量和物理工具位置变化量之间的比值。

Kec=‖ΔF‖/‖ΔX′‖

(49)

式中，Kec为等效接触刚度；ΔX′为相邻两个采样时刻的力觉交互设备末端位置向量的变化量投影到ΔF方向上的分量。

(50)

式中，i为仿真时刻时间标记；Xp(i)为当前采样时刻下力觉设备的位置向量；Xp(i-1)为前一采样时刻下力觉设备的位置向量；F(i)为当前仿真时刻的虚拟力向量；F(i-1)为前一时刻的虚拟力向量。

【限制参量2动态单边约束的位置坐标变化梯度(GradientofPosition，GP)】 相邻两个仿真时刻下，动态单边约束的参考点位置变化量。

ΔX0=X0(i)-X0(i-1)

(51)

式中，ΔX0为位置坐标变化梯度；X0(i)为当前采样时刻下动态单边约束的参考点位置；X0(i-1)为前一采样时刻下动态单边约束的参考点位置。

【限制参量3动态单边约束的法线向量变化梯度(Gradientofnormalvector)】 相邻两个仿真时刻下，动态单边约束的法线方向变化量。数学表达为

Δn0=n0(i)-n0(i-1)

(52)

式中，n0(i)为当前采样时刻下动态单边约束的法线方向；n0(i-1)为前一采样时刻下动态单边约束的法线方向。

从以上限制出发，本研究团队提出基于弹簧力模型的稳定条件(Stability Condition for Spring Force Model，SCSFM)。

基于Colgate[13]等学者提出的Z-Width准则，本研究团队提出基于等效阻抗的稳定性处理算法(Equivalent Impedance Based Stability Algorithm)。通过检测交互设备的位置变化和期望输出力，对交互算法的模拟输出刚度进行估计，使输出刚度不超出设备允许范围，从而保证系统工作在稳定状态[32]。

(53)

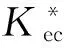
3.3 牙齿交互稳定性试验

牙科手术模拟(Dental Surgery Simulation)中的力觉合成(Haptic Rendering)必须真实反映牙科操作工具和牙齿在不同交互方式下的作用力。基于触力觉反馈的牙科手术培训系统(Haptic-Enabled Dental Training System)的技术要求如下[14]。

【技术要求1典型手术模拟】 牙齿表面具有牙釉质、龋坏组织、牙结石等物理组织；牙齿内部具有牙本质、牙骨质、牙髓腔等多种生物组织。牙科典型手术模拟应包括牙面龋坏组织探查、牙体预备、牙齿纵截面多组织属性感知等。

【技术要求2力觉感受逼真】 牙齿具有复杂几何外形和微小几何特征，内部具有多种物理组织。牙科手术模拟，要求能够感知细微几何特征(如咬合面的窝沟变化)，能够感知龋坏和健康组织之间的属性差异，能够感受逼真钻削过程的力觉效果和视觉效果。

【技术要求3粒度交互控制】 牙齿的数据模型既要支持全局场景(如整个口腔内多颗牙齿)的快速触觉交互，还要支持局部场景(如针对单颗牙齿局部龋坏区域)的细腻触觉交互。

针对牙科手术培训需求，本研究团队开发了基于力觉-视觉反馈通道感觉融合的牙科手术训练样机(Haptic-Visual Collocated Dental Training System，HVCDTS)。该系统能够提供手眼协调操作训练模式，给受训医生提供更加接近临床的训练环境，使受训医生不仅能够看到正在操作的虚拟牙齿，还可以看到握持的虚拟手术工具(探针)，以及进行操作的自己的手，从而能更好地学习正确的手部位形，控制操作力度。

为建立基于力觉-视觉反馈通道感觉融合的牙科手术训练样机(HVCDTS)，实现力觉高保真合成与再现，必须基于物理规律建立交互工具和被操作物体之间的动力学模型。高保真触力觉合成技术，包括虚拟环境建模方法、接触状态检测和确定算法、动力学响应算法等。具体而言，力觉合成技术研究的问题包括以下4个方面：

(1) 人的运动如何映射为虚拟工具的运动，如何建立不同动作下的接触动力学模型，包括法向接触力、表面摩擦力、切削力和力矩等多维力觉分量；

(2) 针对可变形体，如磨削、弹性变形等操作，需要研究形变后被操作物体数字模型的实时快速重构算法；

(3) 如何准确地建立变形和作用力之间的非线性模型；

(4) 为了反映被操作物体表面的纹理接触感觉，以及力觉细节信息(例如龋齿的龋坏孔洞和粘滞效应)等，需要研究具有真实感的力觉合成算法，以便增强精细力觉信息的模拟真实感。

针对上述4个方面的问题，从稳定性的要求出发，本研究团队研究了大数据量虚拟环境下的力觉合成算法稳定性问题，针对不同物理组织的力觉合成问题，针对磨削、弹性变形等操作的物体拓扑结构稳定模拟问题。

3.3.1 复杂场景下的稳定性分析

牙科手术培训的重点是医生手部精细操作能力的训练，虚拟牙齿所提供的精细力觉感受，必须建立在拥有大量数据的精细模型基础之上。全口下牙列精细三角片网格模型含顶点数超过10万，面对数量如此巨大的模型，现有方法无法满足30 Hz图形实时绘制，以及1 kHz的力觉合成要求。数据量小的简单模型虽然能满足视觉和力觉合成的实时性，但逼真度难以保证。

本研究团队提出速度驱动的离散多层级模型力觉合成算法(Discrete LOD Haptic Rendering Algorithm)[37]，离线建立物体层次模型，通过用户探查试验确定触发层次切换的速度阈值，并运用表面接触点(Surface Contact Point，SCP)层级映射改进碰撞检测算法，避免模型层级切换时力信号的振动。

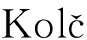
另一方面，在交互过程中，不同交互速度也将带来计算时间复杂度的差异。在碰撞检测(collision detection)算法中，若用HIPi代表本次仿真循环的力觉设备点位置，用SCPi-1代表上次仿真循环结束时虚拟工具点的位置，可定义本次仿真循环的轨迹线段长度

li=|HIPi-SCPi-1|

(54)

则

li=T·vi

(55)

式中，vi为本次仿真循环的人机交互速度(即交互设备运动速度，也即人手速度运动)的大小；T为相邻仿真循环的时间间隔。

式(55)表明，轨迹线段的长度与人机交互速度成正比。人手移动交互设备末端杆的速度越快，一个采样周期内虚拟工具点的运动轨迹线段就越长，参与碰撞检测计算的三角片数量就会增加，从而延长了力觉循环所需要的时间，从一定程度上影响交互系统的实时性和逼真性。以满足力觉合成实时性为前提(力信号刷新频率大于1 kHz)，模型可支持的最大交互速度与该模型的复杂度相关。因此可以得到以下结论，交互速度越快，能支持的模型复杂度越低，即交互速度和模型的复杂度呈减函数关系。

由于交互速度与模型的复杂度两者之间的准确规律未知，基于离散LOD的思想，本研究团队提出速度驱动的离散LOD切换模型，其中层级0为最精细层级，层级精细程度随序号增加而递减(见图24)。

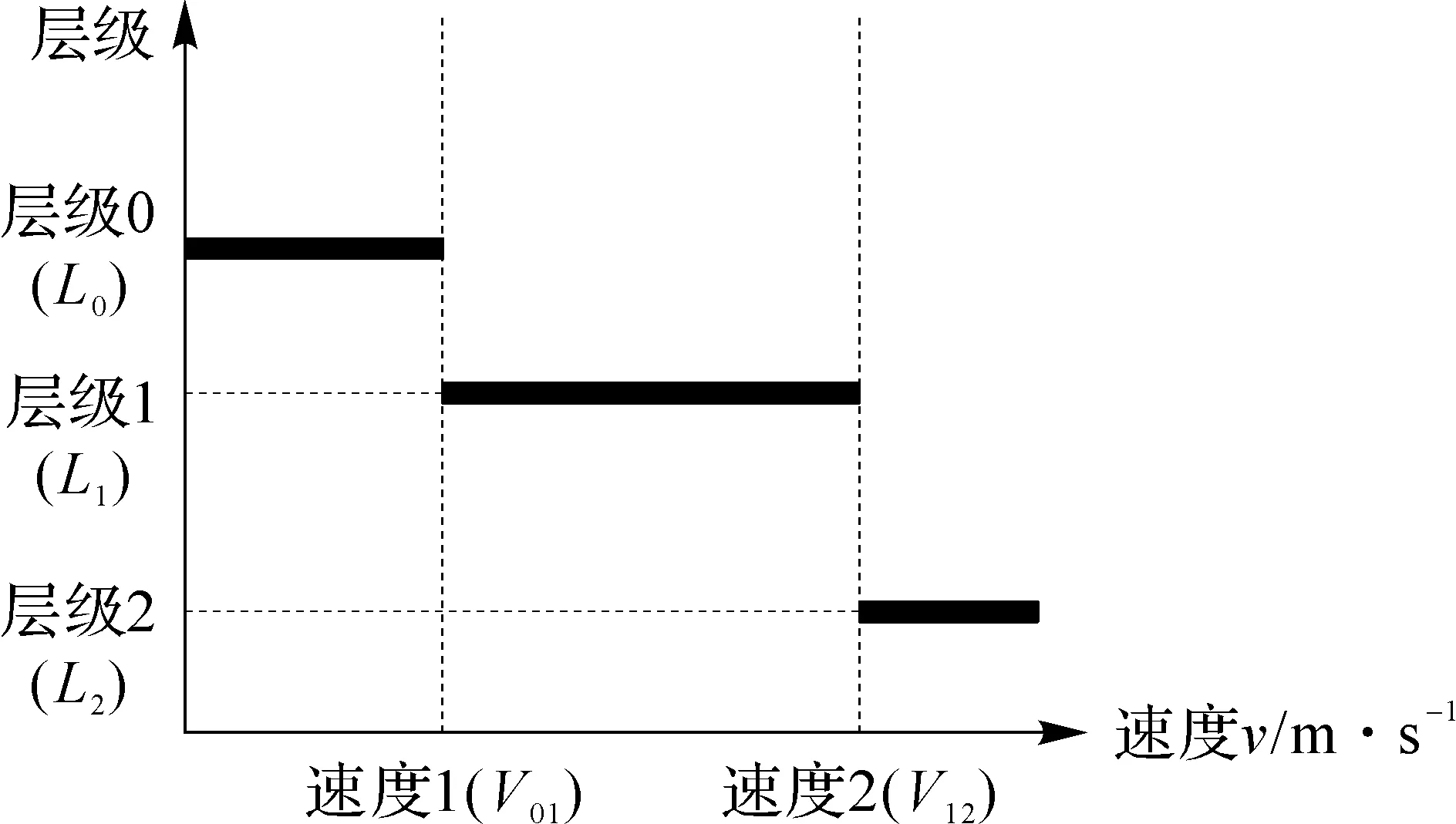
图24 速度驱动的离散LOD切换模型

图24中设定为3个层级，实际应用中层级精度可根据具体任务的模型精度需求预先给定，速度参数则根据层级模型由实验确定。首先通过对给定层级的模型进行力觉交互实验，确定能满足每种模型交互实时性需求的速度阈值，从而确定模型切换的速度。

例如，3个层级需要两个层级切换速度，分别为L0(层级0)和L1(层级1)之间的切换速度V01，L1(层级1)和L2(层级2)之间的切换速度V12。在仿真系统中应用速度驱动LOD力觉合成算法时，当速度小于等于V01时，调用最精细的层级L0；当速度大于V01小于V12时，调用中间层级L1；当速度大于等于V12时，调用最粗糙的层级L2。

(56)

基于上述层级调度模型(见式(56))，在力觉伺服线程中，首先计算交互速度，根据交互速度解算出目标层级的序号，将该层级设置为当前交互的模型对象，根据交互工具的运动信号，进行碰撞检测、碰撞响应计算，从而实现LOD速度驱动模型。

在速度驱动的离散LOD切换模型验证实验中，发现在接触交互发生LOD层级切换时，操作者可以感受到明显的振动。经过分析，发现振动来源于不同层级的三角片网格之间存在形状误差，导致碰撞响应求解失败。

本研究团队认为，造成碰撞响应求解失败的具体原因是，在力觉合成流程中，若上一时刻碰撞发生，则设定当前的交互状态处于碰撞发生阶段，当前时刻应该继续执行碰撞响应模块，此时应根据上一仿真循环结束时的虚拟工具点位置SCPi-1，基于其所从属的几何元素，向其周边几何元素局部扩展的计算，求解新的表面接触点(SCP)。然而，由于上一时刻的SCPi-1位于Li-1的几何元素上，而该几何元素可能在多分辨率模型建立的网格简化过程中受到过简化，且不同层级的几何元素有着不同的拓扑结构，从而导致在局部扩展时无法定位到新的周边几何元素，导致碰撞响应阶段的SCP求解错误，从而导致力信号的突变，引起振动。

因此，需要在目标层级从Li-1切换到Li的同时，将位于Li-1上的SCPi-1点向Li做映射，求解SCPi，从而保证层级切换时碰撞响应求解的正确性，即SCP始终在一个连续的三角片网格表面进行邻域搜索。更进一步地，在三角片网格层级设计时，需要考虑层级几何形状差异对于稳定性的影响。当交互速度降低，在越过某个切换速度时，接触交互LOD模型将从较为粗糙的Li-1切换到较为精细的Li。如果两个层级的三角片网格形状差别过大，这种切换将会导致HIP到三角片网格表面的嵌入深度会发生较大突变，从而产生力信号的突变，导致系统振动(见图25)。因此需要保证层级之间较小的几何误差。

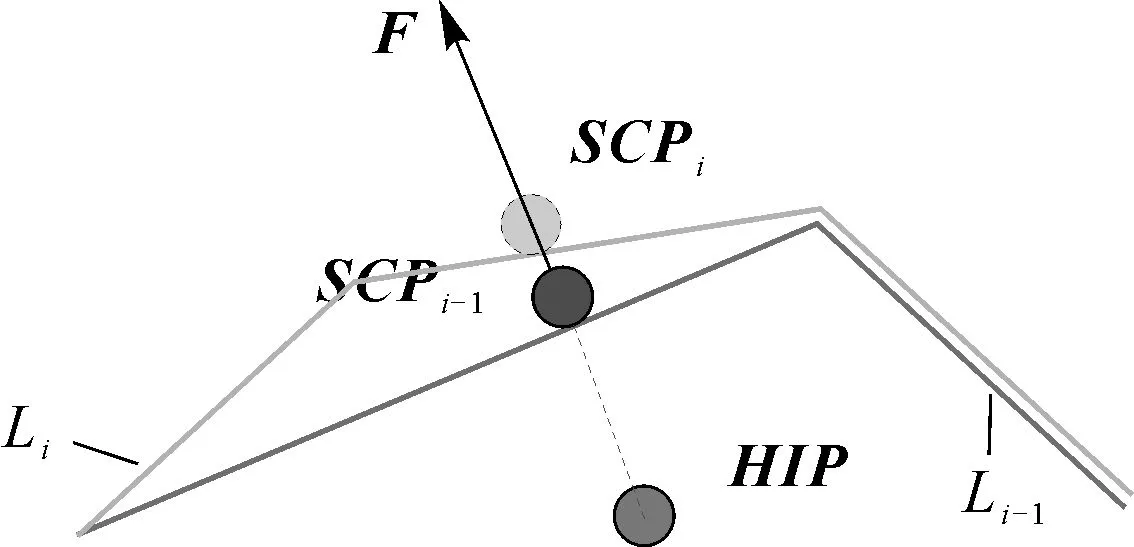
图25 LOD切换中的SCP层级映射

基于上述分析，本研究团队提出一种SCP层级映射算法(SCP Mapping Method)(见图26)。为方便描述问题，进行如下定义。

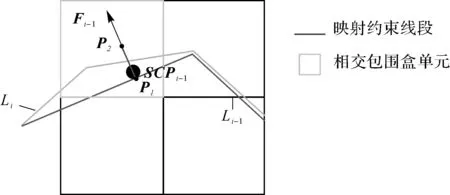
图26 映射约束线段与映射约束包围盒单元

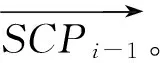
若映射约束线段的起点为SCPi-1，方向沿n，线段的长度为l，则可解算出映射约束线段P1P2(见图26)

P1=SCPi-1

(57)

P2=SCPi-1+l·n

(58)

【定义3映射约束包围盒单元(BoundingBoxofMappingConstraint)】 在所有预定义的空间分割包围盒单元中，与映射约束线段相交的包围盒单元(见图26)。

为了计算位于Li上的SCPi点，需要计算P1P2与Li三角片网格的交点，首先应该获取与P1P2相交的包围盒，然后根据三角片网格与包围盒之间的关联关系，将遍历相交包围盒中的三角片与P1P2求交计算得到SCPi。

在三角片网格初始化时，针对网格所占据的空间，划分出均匀大小的空间分割包围盒单元集合[15]。针对每一个单元，可以求解出其形心在世界坐标系下的体素坐标。在力觉合成计算时，根据P1和P2的绝对坐标，首先计算出其对应于空间分割包围盒的体素坐标P1(n1x,n1y,n1z)，P2(n2x,n2y,n2z)，然后计算包围盒对象的两个角点，利用触力觉开发软件包(GHOST SDK)(Sensable Inc.开发)的求交函数，对这两个角点内的所有体素进行遍历，记录相交体素为一个相交包围盒单元，所有相交包围盒单元构成映射约束包围盒集合。

SCP层级算法流程如下：

[step1] 设置映射约束线段长度为L；

[step2] 根据SCPi与Fi-1构造映射约束，并求解映射约束包围盒集合；

[step3] 遍历包围盒中所有关联三角片，判断三角片与映射约束线段是否相交：

if相交，then记录交点为目标层级Li上的SCPi，同时设置映射发生标志为真；

if不相交，then判断包围盒遍历是否结束：

[判断2] 否则，返回step 3继续遍历包围盒中关联三角片。

分析上述算法可以看到，正确设置映射约束线段的长度L对于提高算法效率非常重要。过大的L会无谓增加映射约束包围盒单元，增加三角片遍历和求交计算的耗时；过小的L可能导致SCPi解算为空，错误设置映射发生标志进入碰撞检测计算模块，此时的碰撞检测计算结果将误判为碰撞分离，会使得层级切换时交互力不连续。L的取值应略大于层级间模型的误差值最为合适，以下牙列交互为例，不同层级之间的误差最大值为2 mm,本文通过实验确定了L的合适取值为5 mm。

本研究团队对单排牙列的离散LOD模型(见图27)进行了接触交互实验。操作者按照不同的移动速度去操作探针接触牙齿，并在牙齿表面滑动。力觉合成程序自动监测操作移动速度，根据上述的多层级力觉合成算法调用不同精细程度的牙齿三角片网格模型进行碰撞检测和碰撞响应计算。

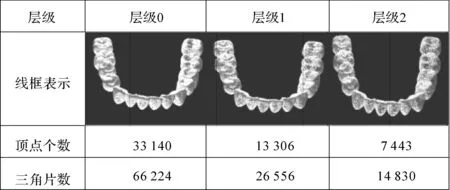
图27 单牙列的离散LOD模型

图28是对单一精细模型层级的接触交互实验结果，图29是对多分辨率层级模型的接触交互实验结果。比较模型的力信号可以看到，速度驱动的多层级模型力觉合成使交互力的振动明显减小。

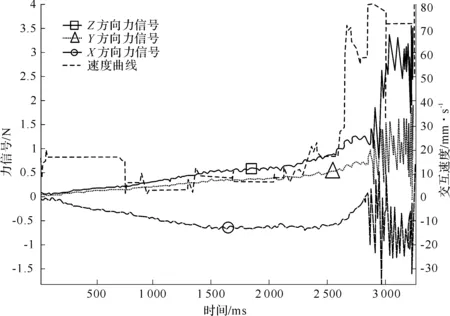
图28 恒定精度模型下的非稳定力觉交互

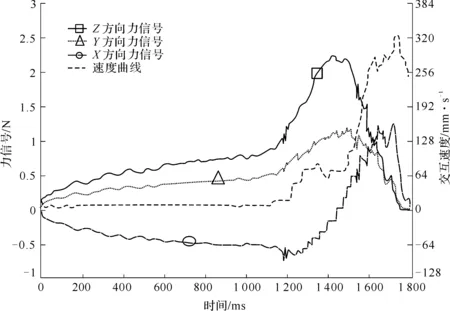
图29 速度驱动的稳定力觉交互

3.3.2 多组织探查力觉合成算法

虚拟环境的交互对象中，存在多组织共存的现象。例如，牙齿包括牙釉质、牙本质、牙髓腔等不同物理属性的组织，在病牙表面存在龋坏组织和正常组织的物理属性差异，等等。如何逼真地模拟这些组织的力觉感知属性差别，并反馈不同组织之间的边界信息，是力觉合成算法研究的一个重要问题。在两种不同物理属性的组织的交界处交互时会产生力觉交互设备的振动，这种振动严重影响到交互的逼真度[39]。

本研究团队提出了适用于不同类型组织边界的力觉合成方法[40]。针对组织之间的模糊边界，提出了灰色区域法(Grey Region Method)(见图30)。

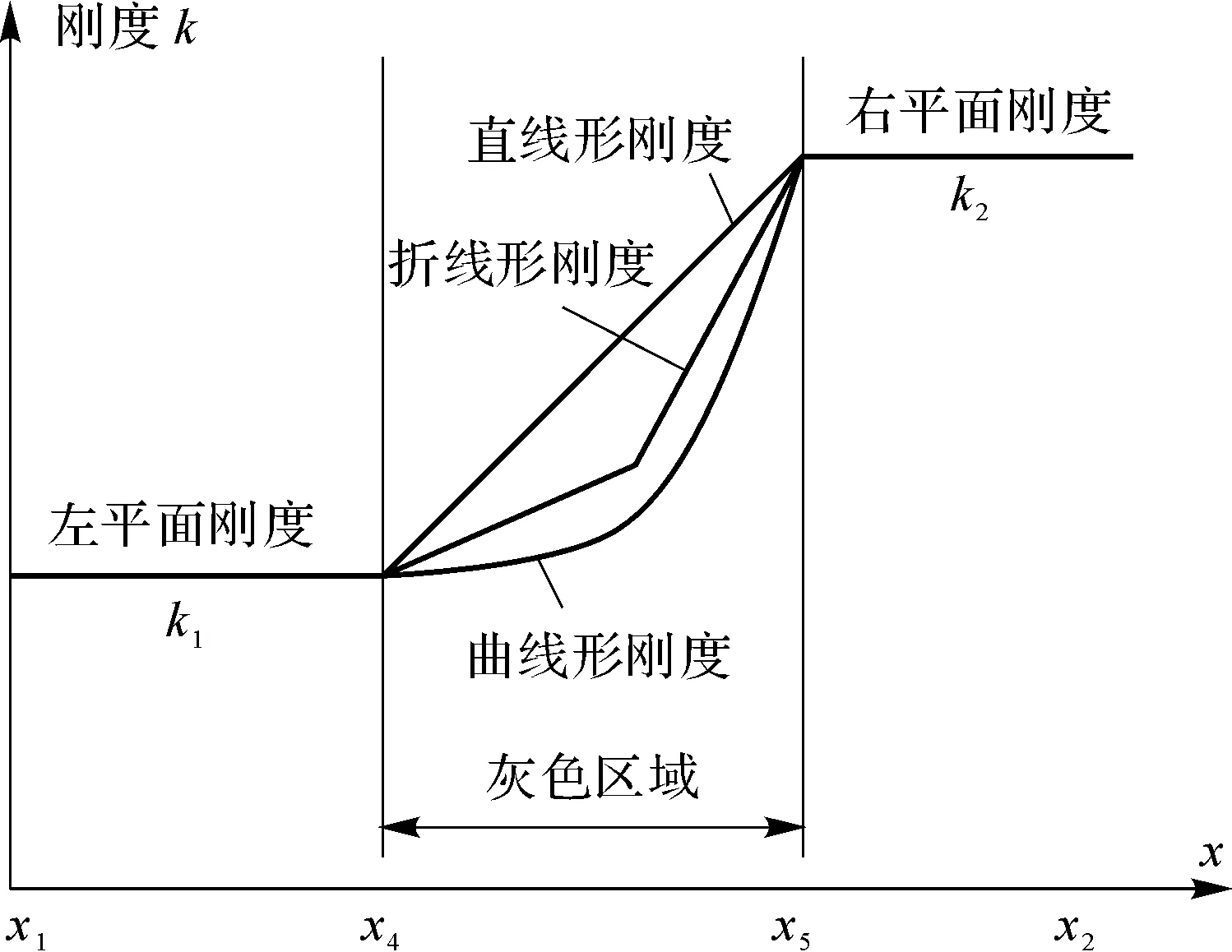
图30 灰色区域法

图30中直线型刚度的计算公式如下。

(59)

式中，k为灰色区域内某一点的虚拟刚度；k1为低刚度的左平面刚度值；k2为高刚度的右平面刚度值；x为物理工具点的坐标；x4和x5为灰色区域的边界坐标。

针对折线形刚度，选择中间位置xmiddle和中间刚度kmiddle，则定义灰色区域的刚度

(60)

针对曲线形刚度k=f(x)，可以选取的曲线形式有很多种，本研究团队采用根据Weber法则推导的用于模拟模糊棱线的灰色区域曲线刚度。

早在1834年，Weber就发现了心理学角度上感知差别大小的Weber法则——能够感知到的刺激的变化值(Δφ)与刺激的初始值(φ)成恒定的比例[41]。

Δφ=cφorΔφ/φ=c

(61)

式中，Δφ为刺激的变化值；φ为刺激的初始值；c为一个常数[41]。

但是，1971年Engen发现当刺激值极小时，Weber分数(Δφ/φ)会增大[41]。尽管Weber法则不是最精确的，但却是最小的刺激值，它提供了一个最大辨别值的极好描述。

在触觉交互中，采用弹簧力模型(spring force model)模拟接触力，则接触力等于弹簧刚度乘以工具嵌入平面的深度。

根据Weber法则，操作者能够感受的刚度差异与刚度(k)成正比

Δk′/k=c

(62)

式中，Δk′是10 ms采样周期内刚度的变化值——刚度差距；k为刚度。

则有

Δk′=0.010×Δk/Δt

(63)

式中，Δk为Δt时间内刚度的变化值。

假设，人在感知平面内不同区域的刚度时，尤其在交界处附近，会保持一个恒定的速度。则

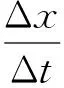
(64)

式中，Δx为操作者位移；Δt为给定时间间隔，v为移动速度。

综合式(62)、式(63)和式(64)，可以写成如下形式

Δk/Δx=(c/0.010v)×k

(65)

将式(65)写成一阶线性微分方程形式

dk/dx+(-c/0.010v)×k=0

(66)

可知该微分方程为齐次线性微分方程，其通解为

k=Ceax
a=c/0.010v

(67)

式中，C为初值；a为中间变量。

因此，C和a均为常量。

由于在x4处的刚度值为k1，在x5处的刚度值为k2。将它们代入式(67)，整理后可以得到

(68)

(69)

式(67)～式(69)即为通过Weber法则推导出的模拟模糊棱线力觉(Indistinct boundary)感受的刚度曲线变化公式。

针对组织之间的清晰边界，本研究团队提出虚拟边界面法(Virtual Boundary Method)(见图31)。为了评价算法的有效性，本研究团队提出棱线清晰度(edge responsiveness)、力觉稳定性(haptic stability)和表面高度变化率(gradient of surface height)等性能评价指标。

图31 平面内不同区域交线处的棱线清晰度示意

棱线清晰度用于描述棱线的清晰程度。棱线清晰度定义为，操作者在交互具有不同物理属性区域的交互对象时，所能判断出的两个区域交线的最小邻域的尺寸。在平面内，棱线清晰度为操作者所能判断的棱线所在的带的宽度(见图31)。在曲面内，棱线清晰度为人所能判断的棱线所在圆管的直径(见图32)。

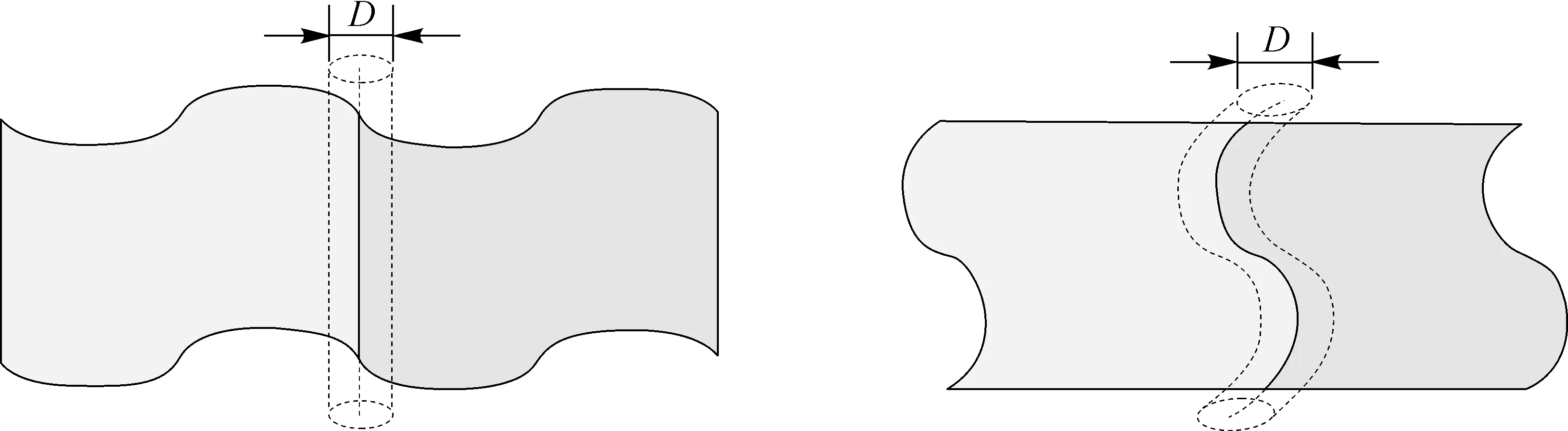
图32 曲面内不同区域交线处的棱线清晰度示意

棱线力觉变化率和表面高度变化率均用来描述交互过程中触觉感受的稳定程度。由于本实验的力觉交互合成方法原始刚度法和灰色区域法均基于弹簧力模型，因此，在交互两个刚度不同的区域的交线时，交互力和工具的嵌入深度不可能同时很小。比如说，前后两个连续的周期中弹簧刚度发生变化，如果工具嵌入虚拟物体表面的深度相同，则交互力一定不相同；反过来，如果前后两个时刻交互力相同，则工具嵌入虚拟物体表面的深度一定不同。因此，要同时考虑在交互的过程中操作者感受到的力的变化和操作者感受到的两个区域的交线处的平面高度的变化。

【定义4棱线力觉变化率(gradientofforcesignalacrossboundary)】 在一次探查过程中，当探查棱线清晰度所在范围内时，交互力的最大变化率。

(70)

式中，ηF为棱线力觉变化率；Ps为工具接触表面的位置点；Ω为棱线清晰度的范围；Fi+1为本次采样周期的输出力；Fi为前次采样周期的输出量。

【定义5表面高度变化率(gradientofsurfaceheight)】 在一次探查过程中，当探查棱线清晰度所在范围内时，表面高度的最大变化率。

(71)

式中，ηH为表面高度变化率；Ps为工具接触表面的位置点；Ω为棱线清晰度的范围；di+1为本次采样周期中工具嵌入模型表面的深度；di为前次采样周期中工具嵌入模型表面的深度。

在一次探查过程中，棱线力觉变化率和表面高度变化率越小，则探查时操作者感受到的稳定性越好。

在模糊棱线力觉的模拟中，棱线清晰和触觉感受的稳定是不能同时保证的。因为，如果交线处的交互力和表面的高度的变化在探查表面时都不能被发现，操作者就不会在表面上发现一个刚度不同的两个区域的交界线。然而，对于具有不同物理属性的多组织交互对象的模糊的交界线，操作者并不会去关心交界线的位置和形状，而只是在意渐变的力觉感受。因此，对于具有模糊棱线的交互对象的力觉合成，操作者关注两个稳定性指标(即棱线力觉变化率和表面高度变化率)，稳定性越高越好。

为了验证灰色区域法的有效性，本研究团队设计了模糊棱线探查实验，用于衡量灰色区域的方法对具有不明显交界的刚度不同的多组织表面探查的合成效果。

实验系统由一台计算机和一台触觉交互设备组成(见图33)。计算机配置为Intel P4 2.8 G，内存为DDR 1 G，触觉交互设备为Phantom desktop。

图33 实验平台系统照片

实验的虚拟平面上设置两个刚度不同的区域。实验平面的尺寸为100 mm×100 mm，左半平面刚度为2.0 N/mm，右半平面刚度为0.5 N/mm。设置一个宽度为40 mm的灰色区域。

图34和图35记录了每个触觉循环周期内输出的接触力F(N)、工具设备末端点嵌入平面的深度d(mm)和接触位置的刚度k(N/mm)。工具先从平面的左端滑动到右端，记录中间交线附近的数据见图34(a)和图35之左图，工具再从平面的右端滑动到左边，记录中间交线附近的数据见图34(b)和图35之右图。横轴是时间轴，它的刻度表示采样周期序列，每个采样周期的时间是30 ms。

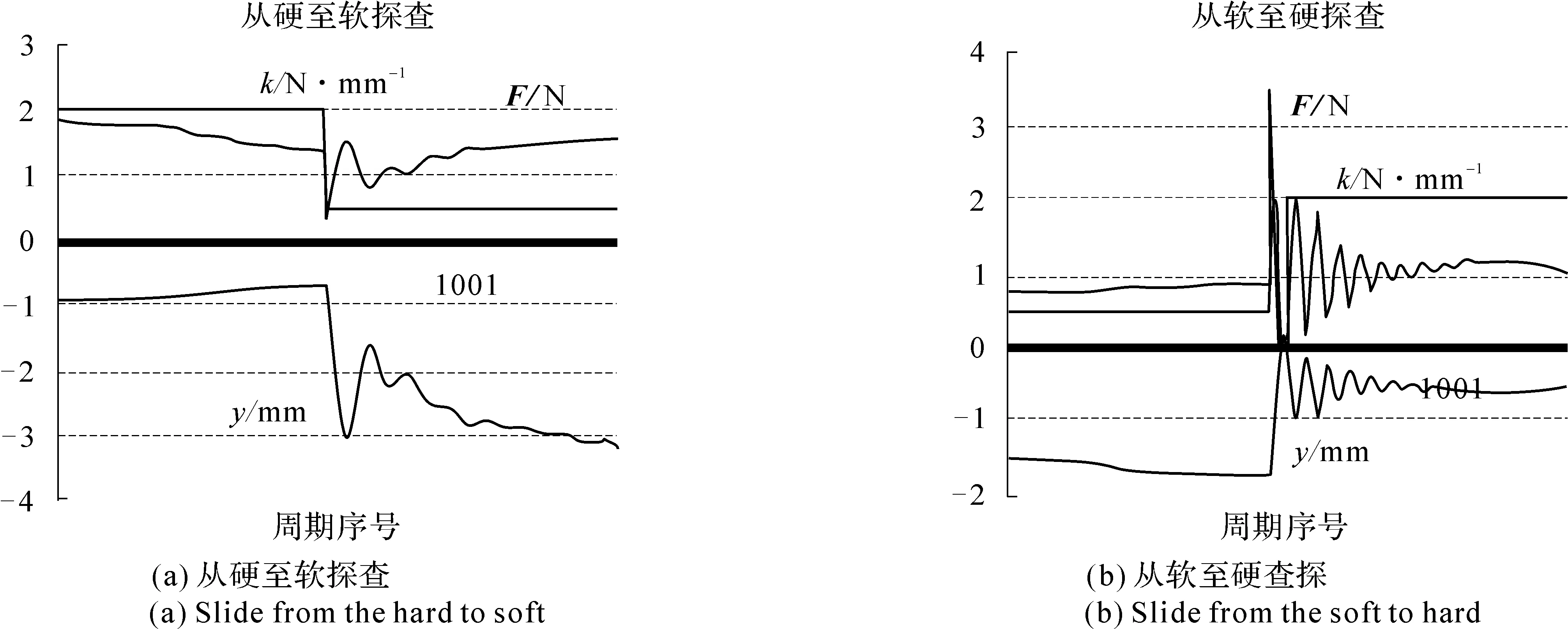
图34 采用原始刚度探查交线处的力、位置信号

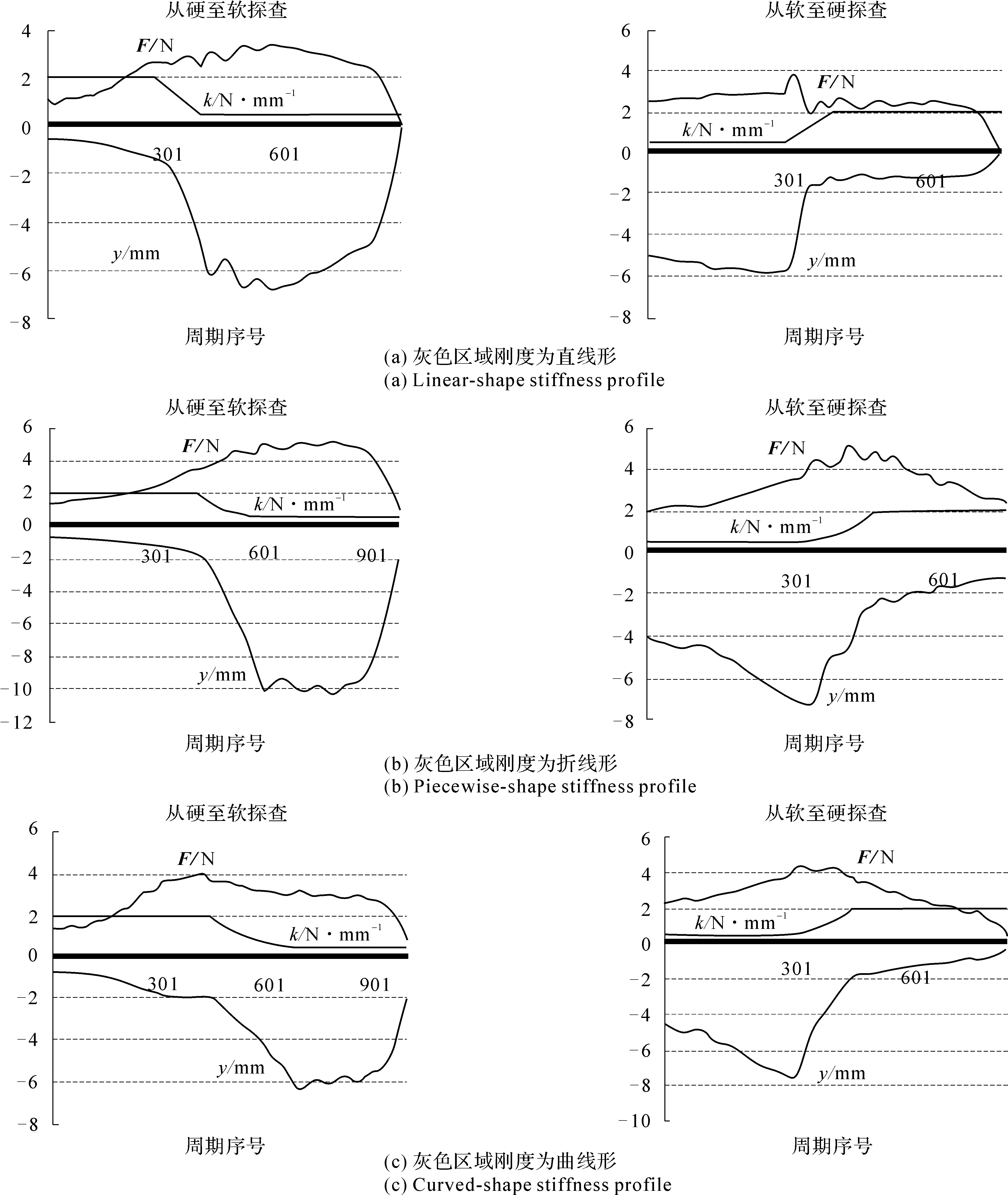
图35 采用灰色区域法探查交线处的力、位置信号

在图34中可以发现，在刚度发生变化的时刻附近，接触正压力曲线和工具点的位置曲线发生剧烈的振动。在图35中，接触正压力曲线和工具点的位置曲线，始终是比较平稳的变化。实验的过程中，操作者的感受是当采用原始刚度法合成时，在软硬区域交界处附近，会感受到剧烈的机械振动，甚至会导致触觉交互设备的通讯中断。当采用灰色区域法进行合成时，不会感受到非常明显的机械振动。可见，实验者的感受与图34和图35数据反映的现象是一致的。

另外，从图34中记录的接触正压力曲线和工具点的位置曲线可以发现，当工具从较软的区域向较硬的区域运动时的振动，比工具从较硬的区域向较软的区域运动时的振动强烈。

以棱线力觉变化率和表面高度变化率作为衡量指标，用式(63)和式(64)对图34和35中的数据计算，计算结果见图36和图37。

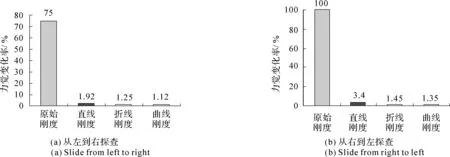
图36 采用原始刚度与采用灰色区域法得到的力觉变化率的对比

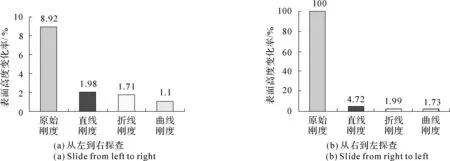
图37 采用原始刚度与采用灰色区域法得到的表面高度变化率的对比

对比原始刚度法和灰色区域法，模拟模糊棱线的力觉感受，从图36和图37中可以看出，采用原始刚度法比采用灰色区域法得到的力觉变化率高、表面高度变化率高。因此，采用灰色区域法得到的模糊棱线的探查感受比采用原始刚度法稳定性好。另外，对比灰色区域法中的直线刚度、折现刚度和曲线刚度三种方法，从图36和图37中可以看出，采用曲线形刚度比采用折线形刚度交互的稳定性更好，而采用折线形刚度比采用直线形刚度更好。

对于棱线清晰度，如果采用原始刚度法，则在软硬区域交界处触觉交互设备会发生剧烈的振动，操作者据此可以很容易的判断出交界的位置。如果采用灰色区域法，刚度是在逐渐变化的，操作者不会感觉到明显的机械振动，但是可能会感觉到有一条斜坡的棱线(直线刚度的灰色区域法这种感觉相比折线和曲线刚度明显)，操作者只能判断交界的位置在灰色区域中的某一处。因此，得到的棱线清晰度的结果见图38。

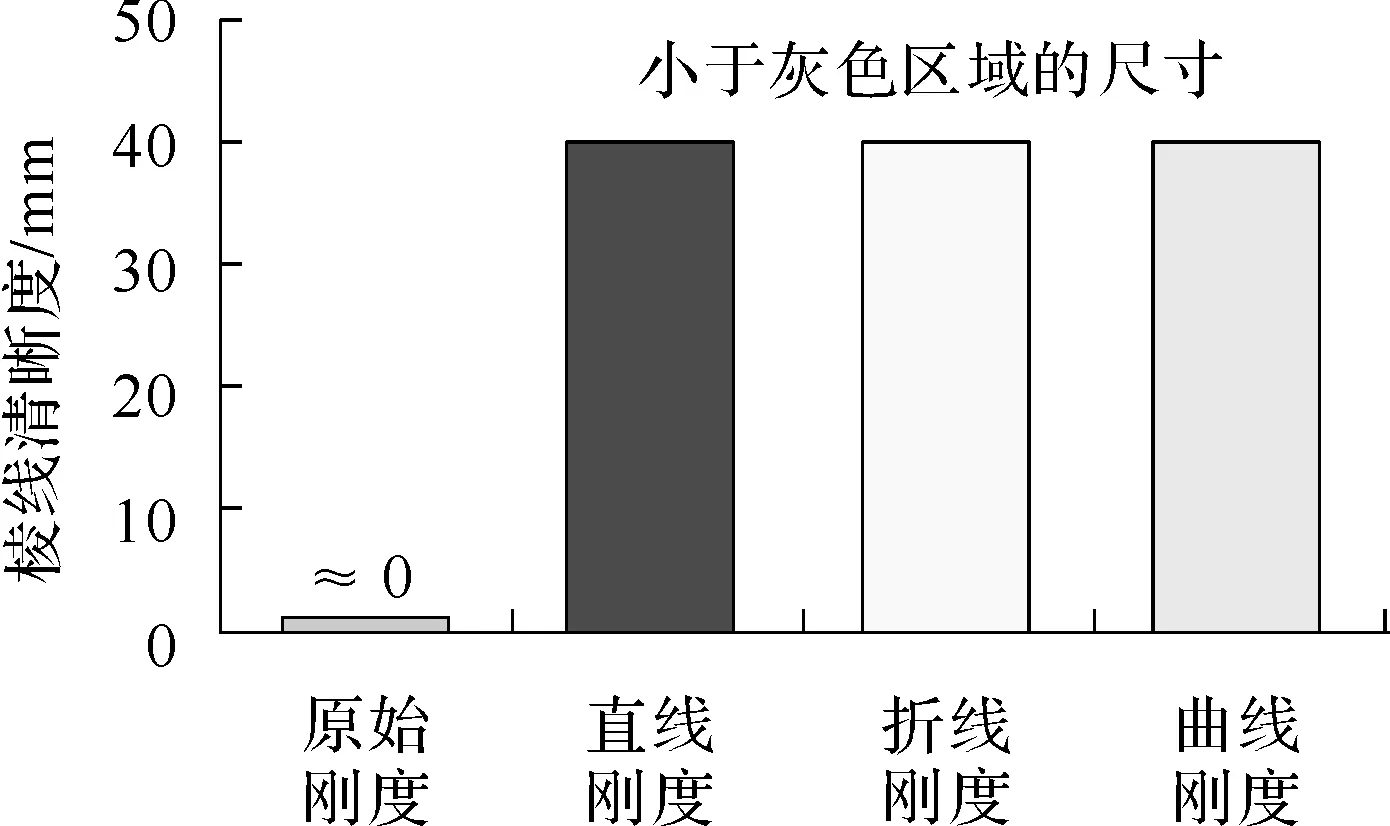
图38 采用原始刚度与采用灰色区域法得到的棱线清晰度的对比

从实验过程中操作者的感受来说。采用灰色区域的方法(直线形刚度、折线形刚度和曲线形刚度)比采用原始刚度的方法，交互时更加稳定，尽管软硬区域的交线会变得不明显。对比灰色区域法的3种方法，感受整个平面的刚度变化，可以发现，采用直线形刚度时，在灰色区域附近可以感受到有一个斜坡，并且在斜坡的底端有一条较为明显的棱线。然而在采用曲线形刚度时，这种斜坡的感觉以及斜坡与软区域交界处的棱线的感觉最弱。采用折线形刚度时，触觉的效果在采用直线形刚度和采用曲线形刚度之间。

可见，操作者在实验过程中对于棱线附近的探查感受和图36、图37和图38数据反映的结果是相同的，并且这种关于稳定性的力觉感受与Weber法则是相符合的。

通过本实验所得数据和操作者的感受，可知灰色区域的方法用于模拟模糊棱线的力觉感受是有效的。

本研究团队以牙齿横切面的多组织探查和龋坏组织的探查为例进行了实验验证(见图39和图40)。基于操作者主观感受的实验结果表明所提出的算法可以满足逼真的组织边界显示要求，并可以保证交互稳定性。在探查牙齿切面实验中，操作者用虚拟工具在牙齿切面上滑动，当工具从较软的牙本质向较硬的牙釉质滑动或者从最软的牙髓向较软的牙本质滑动时，虚拟工具会勾在不同组织的交界上。因此，操作者可以很清晰的找到不同组织之间的交线。并且，在这个过程中没有明显的机械振动。

(a) boundary between different tissue (b)boudary between enamel and dentin (c) boudary between dentin and dental pulp cavity

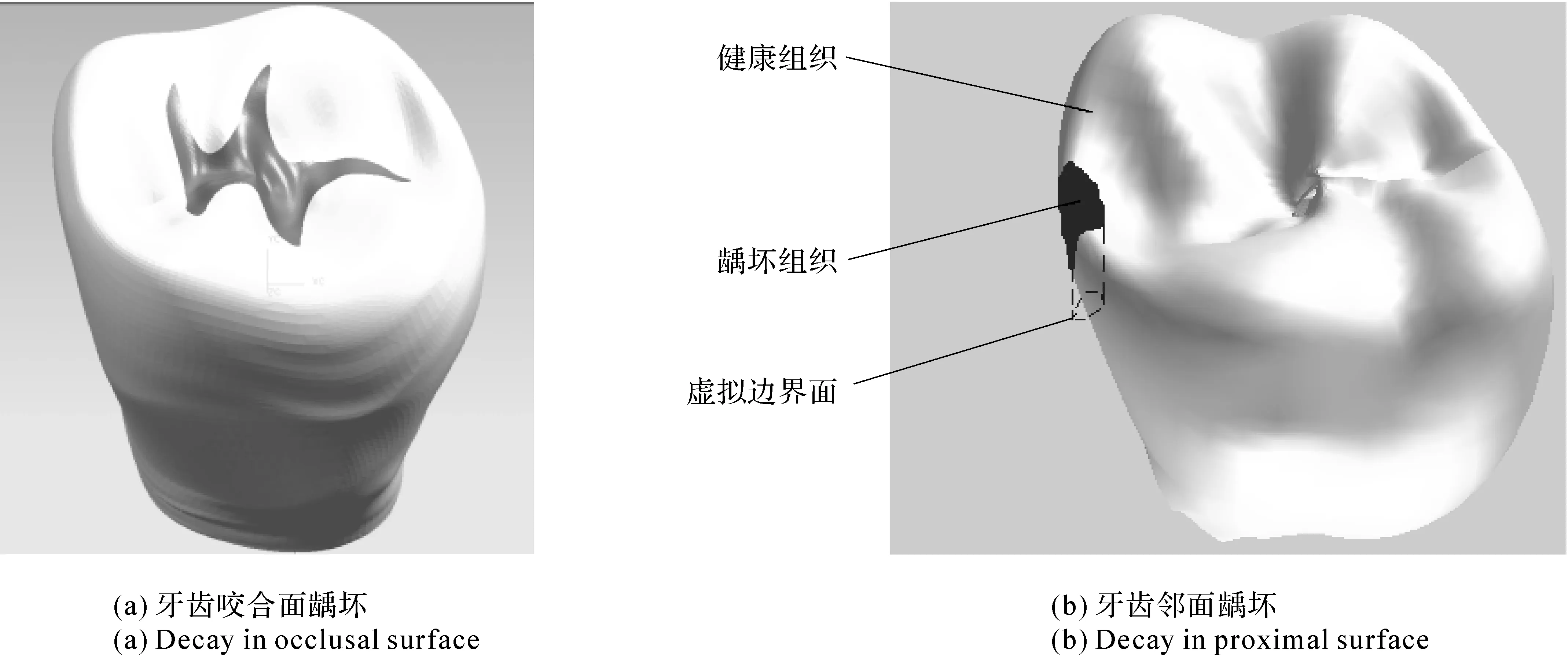
图40 龋坏组织的探查

3.3.3 拓扑结构可变的力觉交互算法

在力觉交互问题中，某些牙科操作(例如，钻削、切割等)会引起被操作物体拓扑结构的变化。在传统的力觉交互算法中，交互力计算依赖于被操作物体的拓扑结构，因此导致产生计算闭环效应，即在物体模型更新瞬间，交互设备往往会出现振动、噪声等失稳现象。设计既实现逼真力觉感受，又保证交互稳定性的力觉合成算法，是研究难点。

本研究团队对牙齿以及工具进行体素化建模(volume modeling)(见图41和图42)，并基于模型体数据进行力觉计算和图形绘制，与面网格与体数据混合模型相比，可以避免材料去除时面模型的实时重构，有利于简化算法，增强计算效率[42]。

图41 牙齿的体素模型

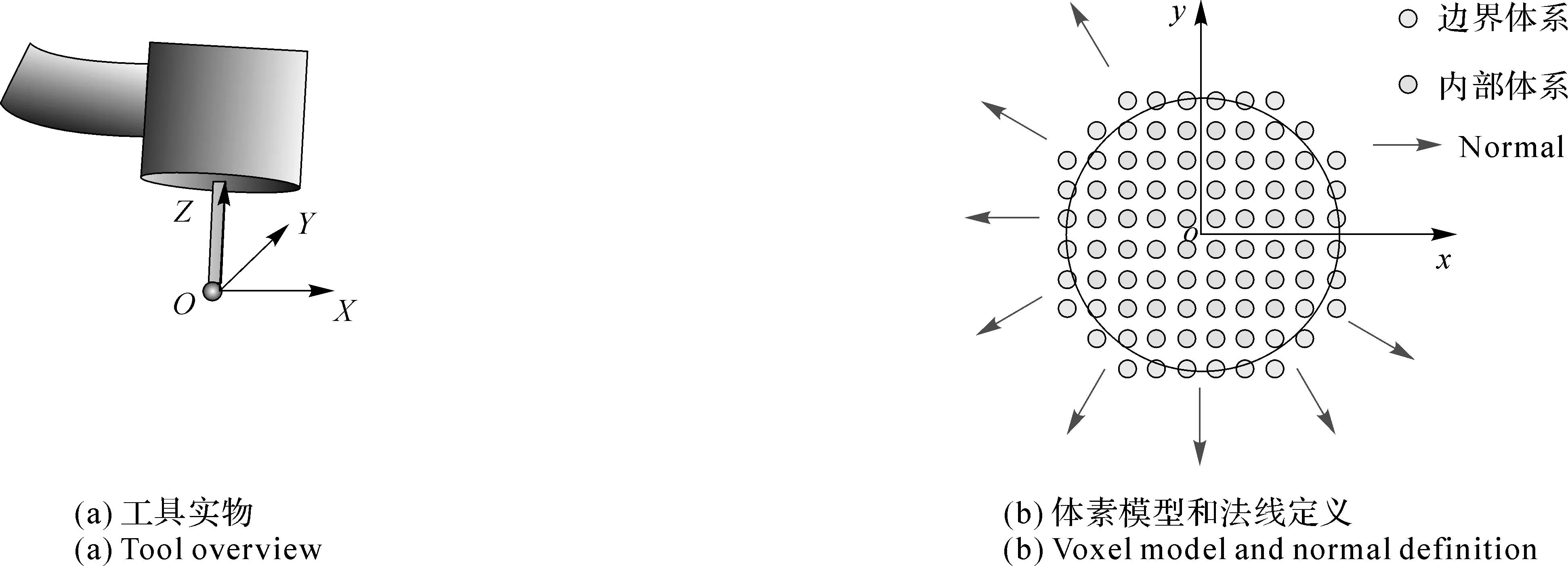
图42 工具的体素模型

文献[43-45]对骨骼切削模拟的研究主要通过理论模型来建立切削力和刀具进给运动之间的关系。由于牙齿切削尚无现成的理论模型，本研究团队采用实验方法测量了切削力与速度的关系[46]，建立了近似的切削力模型[47]，通过合理定义接触面积，避免了材料去除时接触面积的突变。

(72)

(73)

式中，N为钻针的旋转速度；D为接触面积；s为面积积分微元；u(s)为单位切削能；r(s)为微元到钻针轴线的径向距离；nn(s)为接触点的法向量；nt(s)为接触点的切向量；α和μ为被切削材料和钻针的物理参数[41]；T为转置；ds为接触面积微元。

为保证交互稳定性，本研究团队提出了适合于材料去除操作的虚拟匹配算法(Virtual Coupling Method)。

(74)

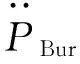
FVC=kVC(PHandle-PBur)

(75)

式中，kVC为虚拟匹配弹簧的刚度，仿真时取一个数值小于力觉设备的最大可模拟刚度；PHandle为物理工具的位置。

钻削过程的力学模型和实验数据见图43～图45。采用0.1 mm的剖分粒度进行牙齿钻削实验，牙齿体素模型可以满足1 kHz的力觉反馈频率和30 Hz的模型重构频率的实时性要求，所设计的模型重构算法可以实现两种不同工具的钻削仿真[47]，可以模拟典型洞型的形状制备，模拟图形效果见图46。

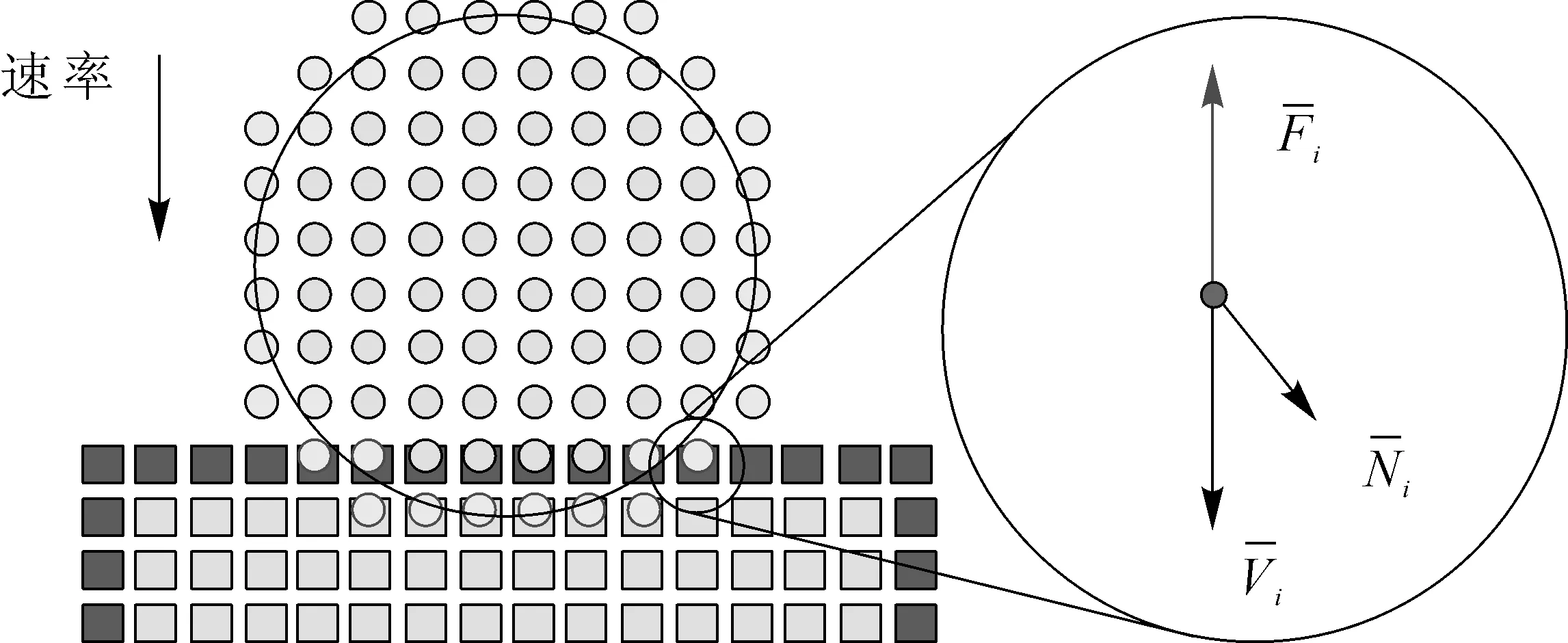
图43 钻削过程的力学模型

图44 材料去除原理

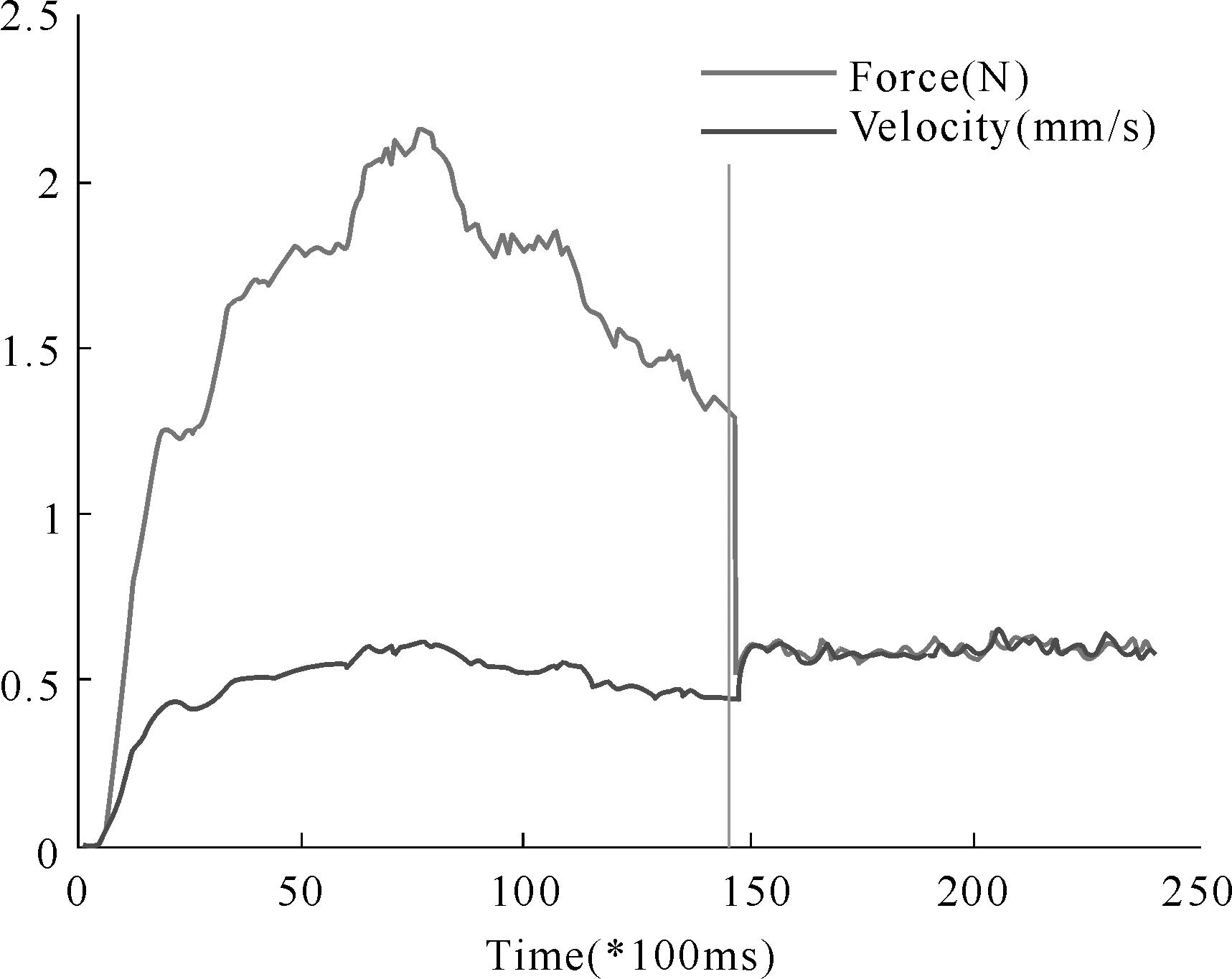
图45 切削力和进给速度曲线

图46 典型洞型的钻削制备

4 结论和展望

本文研究实时力觉交互系统稳定性的失稳机理及稳定性增强方法。文章的主要结论如下：

(1) 通过分析力觉交互系统与人不在回路控制系统的区别，提出了力觉交互系统稳定性问题的分类，基于对系统组成的分析，假定操作者为系统的被动环节，将稳定性问题分解为力觉交互设备和力觉合成算法两部分，通过确定各自的验证任务和验证指标，实现了问题解耦，使得力觉交互系统的设计和调试变得方便易行，对于提高力觉交互系统的稳定性具有实际应用价值。

(2) 在力觉设备稳定性研究方面，讨论了多自由力觉交互设备性能与系统稳定性的关系，建立了力觉交互系统控制参量与系统稳定性的关系模型，提出了提高系统稳定性的控制算法，重点研究了电流闭环控制算法、多更新率系统的稳定性，基于自主开发的力觉交互设备iFeel3开展了稳定性测定试验，得到了工作空间内不同点不同方向上可模拟最大刚度的分布。这些工作对于设计类似力觉交互设备具有借鉴意义。

(3) 在力觉合成算法稳定性研究方面，以交互速度作为驱动变量，提出了适合于复杂场景交互的多层级力觉合成算法，实现了计算实时性与计算稳定性的折中。以提出了一种虚拟平面法，保证了具有不同物理属性多组织交互时力信号的连续性。提出了适合于材料去除操作的虚拟匹配算法，保证了钻削等力觉模拟的稳定性。

(4) 研究结果为开发具有力觉反馈的人机交互系统提供了关键技术和理论依据。以牙科手术训练系统中的典型手术操作为对象，验证了力觉合成算法的稳定性。

未来工作需要进一步研究特殊力觉交互设备，例如基于绳驱动的并联力觉设备的稳定性，以及6维力觉合成算法的稳定性。

[1] Barbagli F，Salisbury K，Prattichizzo D.Dynamic Local Models for Stable Multi-Contact Haptic Interaction with Deformable Objects//Proceedings of the 11th Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems (HAPTICS’03)，Los Angeles，California，USA，2003：109-117.

[2] Seungmoon Choi，Hong Z Tan.An Experimental Study of Perceived Instability During Haptic Texture Rendering：Effects of Collision Detection Algorithm//11th International Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems，2003：197 -204.

[3] Colgate J E，Schenkel G.Passivity of a Class of Sampled-Data Systems：Application to Haptic Interfaces//Proceeding of American Control Conference，Baltimore，USA，1994：3236-3240.

[4] Salisbury K，Conti F，Barbagli F.Haptic Rendering：Introductory Concepts.IEEE Computer Graphics and Applications，2004(March/April)：24-32.

[5] Salisbury C，Gillespie R B，Tan H Z，et al.Effects of Haptic Device Attributes on Vibration Detection Thresholds//Proceedings of the 2009 World Haptics Conference(WHC09)：the Third Joint EuroHaptics Conference and Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems，Salt Lake City，UT，USA，2009：115-120.

[6] Adams R J，Hannaford B.Control Law Design for Haptic Interfaces to Virtual Reality.IEEE Transactions on Control Systems Technology，2002，1(10)：3-13.

[7] Hannaford B，Ryu J H.Time-Domain Passivity Control of Haptic Interfaces.IEEE Transaction of Robotics and Automation，2002，18(1)：1-10.

[8] Brian E Miller，J Edward Colgate，Randy A Freeman.On the Role of Dissipation in Haptic Systems.IEEE Transactions on Robotics，2004，20(4)：768-771.

[9] Adams R J，Hannaford B.Stable Haptic Interaction with Virtual Environments.IEEE Transactions on Robotics and Automation，1999，15(3)：465-474.

[10] Miller B E，Colgate J E，Freeman R A.Guaranteed Stability of Haptic Systems with Nonlinear VE.IEEE Transaction on Robotics and Automation，2000(Dec.)：712-719.

[11] Mahapatra S，Ziefran M.Stable Haptic Interaction with Switched Virtual Environments//Proceedings of the 2003 IEEE Infernational Conference on Robotics & Automation，Taipei，Taiwan，2003：1241-1246.

[12] Gil J J，Avello A，Rubio，et al.Stability Analysis of a 1 DOF Haptic Interface Using the Routh-Hurwitz Criterion.IEEE Transactions on Control Systems Technology，2004，12(4)：583-588.

[13] Colgate J E，Brown J M.Factors Affecting the Z-Width of a Haptic Display// Proceedings of IEEE International Conference on Robotics and Automation，Los Alamitos，CA，USA，1994：3205-3210.

[14] 王党校，张玉茹，王勇，等.面向牙科手术培训的力觉合成技术.中国科学[F]，2009，39(1)：159-174.

WangDangxiao，Zhang Yuru，Wang Yong，et al.Haptic Rendering for Dental Training System.Science in China[Series F]，2009，39(1)：159-174.

[15] Gillespie B，Cutkosky M.Stable User-Specific Rendering of the Virtual Wall//Proceedings of the ASME International Mechanical Engineering Conference and Exposition(DSC-Vol.58)，Atlanta，GA，USA，1996：397-406.

[16] Adams R J，Hannaford B.Stable Haptic Interaction with Virtual Environments.IEEE Transactions on Robotics and Automation，1999，15(3)：465-474.

[17] 罗杨宇.力觉交互系统建模分析与设计方法研究[博士学位论文].北京：北京航空航天大学，2003.

Luo Yangyu.Modeling and Design of Haptic interaction Systems[PhD.Thesis].Beijing：Beijing University of Aeronautics and Astronautics，2003.

[18] Masayuki Kawai，Tsuneo Yoshikawa.A new Haptic Interface Device Capable of Continuous-Time Impedance Display within Sampling-Period:Application to Hard Surface Display//Proceedings of IEEE International Conference on Robotics and Automation，2001，1：880-885.

[19] Mehling J S，Colgate J E，Peshkin M A.Increasing the Impedance Range of a Haptic Display by Adding Electrical Damping//Eurohaptics Conference and Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems，2005，World Haptics，2005：257-262.

[20] Ryu Jee-Hwan，Preusche C，Hannaford B，et al.Time Domain Passivity Control with Reference Energy Following.IEEE Transactions on Control and System Technology，2005，13(5)：737-742.

[21] Abdossalami A，Sirouspour S.Adaptive Control for Improved Transparency in Haptic Simulations.IEEE Transactions on Hpatics，2009，2(1)：2-14.

[22] Juan G J，Emilio S.Control Algorithms for Haptic Interaction and Modifying the Dynamical Behavior of the Interface//Proceeding of 2nd International Conference on Enactive Interfaces，Genoa，Italy，2005.

[23] Dai X W，Zhang Y R，Cao Y G，et al.Current Closed Loop Control for Increasing Virtual Stiffness in Haptic Interaction//IEEE/ASME International Conference on Mechatronics and Embedded Systems and Applications，Beijing，China，2008：432-436.

[24] Dai X W，Zhang Y R，Cao Y G，et al.Stable Multirate Control Algorithm for Haptic Dental Training System//International Conference on Intelligent Robotics and Applications(2008 ICIRA)，Wuhan，China，2008：27-35.

[25] Kazerooni H，Her M G.The Dynamic and Control of a Haptic Interface Device.IEEE Transactions on Robotic and Automation，1994，10(1)：453-464.

[26] Dai X W，Zhang Y R，Wang D X.Maximum Virtual Stiffness Distribution Analysis and Measurement for Haptic Device//Proceeding of ASME 2009 International Design Engineering Technical Conferences(IDETC) & Computers and Information in Engineering Conference(CIE)，San Diego，CA，USA，2009：915-921.

[27] Abbott J J，Okamura A M.Effects of Position Quantization and Sampling Rate on Virtual-Wall Passivity.IEEE Transaction on Robotics，2005，21(5)：952-964.

[28] Diolaiti N，Niemeyer G，Barbagli F，et al.Stability of Haptic Rendering：Discretization Quantization，Time Delay，and Coulomb Effects.IEEE Transactions on Robotics，2006，22(2)：256-268.

[29] Wang Dangxiao，Zhang Yuru.Effect of Haptic Device’s Position Resolution on Stability//Proceedings of Eurohaptics 2004，Munich，German，2004：377-380.

[30] Wang D X，Zhang Y R，Cao Y G.Dynamic Unilateral Constraint (DUC) Unified model for VE-Induced Instability Analysis in Haptic System//Proceedings of EuroHaptics 2006，Paris，France，2006：2-5.

[31] Hogan N.Impedance Control：an Approach to Manipulation：PartⅡ-Implementation.ASME Journal of Dynamic Systems Measurement and Control，1985，107(March)：8-16.

[32] 王党校，张玉茹，王玉慧，等.约束切换与阻抗显示力反馈设备的稳定性研究.机器人，2004(2)：97-101.

Wang Dangxiao，Zhang Yuru，Wang Yuhui，et al.Constraint Switching and Stability Issues in Impedance Display Force Feedback Device.Robot，2004(2)：97-101.

[33] El-Sana J，Varshiney A.Continuously-Adaptive Haptic Rendering.Virtual Environments，2000，23(2)：135-144.

[34] Otaduy M A，Lin M C.Sensation Preserving Simplification for Haptic Rendering.ACM Trans.Graph.，2003，22(3)：543-553.

[35] Liu Peiran，Shen Xiaojun，Georganas N.Multi-Resolution Modeling and Locally Refined Collision Detection for Haptic Interaction//Proceedings of the 5th International Conference on 3-D Digital Imaging and Modeling(3DIM’ 05)，Ottawa，Canada，2005：581-588.

[37] 周万琳，王党校，张玉茹，等.基于速度驱动的复杂场景多层级力觉交互算法.计算机学报，2009，32(8)：1560-1570.

Zhou Wanlin，Wang Dangxiao，Zhang Yuru，et al.Velocity Driven Levels of Detail Haptic Rendering Algorithm for Complex Scenes.Chinese Journal of Computers，2009，32(8)：1560-1570.

[38] Lederman S J，Klatzky R L，Hamilton C L.Perceiving Roughness Via a Rigid Probe：Psychophysical Effects of Exploration Speed and Mode of Touch.The Electronic Journal of Haptic Research，1999，1(1)：311-323.

[39] Burdea G，Patounakis G，Popescu V，et al.Virtual Reality-Based Training for the Diagnosis of Prostate Cancer.IEEE Transactions on Biomedical Engineering，1999，46(10)：1253-1260.

[40] Zhou Renge，Wang Dangxiao，Zhang Yuru.Haptic Rendering of Tissue Boundary for Surgical Training//IEEE/ASME Advanced Intelligent Mechatronics，Xi’an，China，2008：949-954.

[41] Gescheider G A.Psychophysics:the Fundamentals(Third Edition).London：Lawrence Erlbaum Associates，1997：3-8.

[42] Wang D X，Zhang Y R.Cutting on Triangle Mesh Local Model Based Haptic Display for Dental Preparation Surgery Simulation.IEEE Transaction on Visualization and Computer Graphics，2005(6)：671-683.

[43] Morris D，Sewell C，Barbagli F，et al.Visuohaptic Simulation of Bone Surgery for Training and Evaluation.IEEE Computer Graphics and Applications，2006，26(4)：48-57.

[44] Agus M，Giachetti A，Gobbetti E，et al.Real-Time Haptic and Visual Simulation of Bone Dissection//Presence：Teleoper Virtual Environ，2003，12(1)：110-122.

[45] Tsai Ming-Dar，Hsieh Ming-Shium，Tsai Chiung-Hsin.Bone Drilling Haptic Interaction for Orthopedic Surgical Simulator.Computers in Biology and Medicine，2007，37(12)：1709-1718.

[46] Liu Guanyang，Zhang Yuru，Wang Dangxiao.Townsend，Stable Haptic Interaction Using a Damping Model to Implement a Realistic Tooth-Cutting Simulation for Dental Training.Springer Virtual Reality Journal，2008，12(2)：99-106.

[47] Wu Jun，Wang Dangxiao，Wang C C L，et al.Toward Stable and Realistic Haptic Interaction for Tooth Preparation Simulation.ASME Transactions-Journal of Computing and Information Science in Engineering，2010，10(2)：No.021007.