海气通量涡相关法计算中的时间尺度分析
黄艳松, 宋金宝, 范聪慧
(1.中国科学院 海洋研究所 环流与波动重点实验室, 山东 青岛 266071; 2. 中国科学院 研究生院, 北京100039)
海气通量涡相关法计算中的时间尺度分析
黄艳松1,2, 宋金宝1, 范聪慧1
(1.中国科学院 海洋研究所 环流与波动重点实验室, 山东 青岛 266071; 2. 中国科学院 研究生院, 北京100039)
基于黄海上连续14 d的浮标观测资料, 采用多尺度分解法确定了海气通量涡相关法计算中的截断时间尺度, 并分析了该截断时间尺度的特征及其对感热通量计算的影响。研究结果是:由多尺度分解法获得的湍通量截断时间尺度可将总通量中湍通量和中尺度通量分离开来, 截断时间尺度随着湍流强度或水平风速的增加而增加, 且感热通量的截断时间尺度大于动量通量的截断时间尺度; 在弱湍流状态下(σw<0.3 m/s), 动量通量和感热通量的截断时间尺度主要分布在100 s左右, 湍通量和总通量之间差别较大; 在湍流较强时(σw>0.3 m/s), 动量通量和感热通量的截断时间尺度主要分布在800 s左右,湍通量和总通量之间差别较小; 通过计算和分析不同截断时间尺度下感热通量的平均值和不确定性,可以看出截断时间尺度对感热通量的平均值的影响较小, 但对感热通量的不确定性有很大的影响, 这两种影响之间的差别会随着湍流强度的增加而减小。海气通量涡相关法计算中, 正确的截断时间尺度的选取可以获得真实可靠的海气通量数据, 也为进一步认识和了解上层海洋与大气之间的相互作用提供重要的科学依据。
平均时间尺度; 海气通量; 谱隙; 多尺度分解法; 截断时间尺度
海气通量反映了海洋与大气之间的相互联系与反馈机制, 强烈地影响上层海洋及大气底边界层的结构, 在海气相互作用、海洋-大气耦合模式、表面波与流的预报中起着重要的作用, 近年来受到了越来越多的关注。
随着海上高频观测数据的增多, 涡相关法作为直接计算海气通量的有效方法, 得到了越来越普遍的应用。使用涡相关法计算海气通量存在着一个很重要的问题就是平均时间尺度问题, 即用来计算脉动量的时间尺度, 文献[1]将其定义为截断时间尺度。一方面这个截断时间尺度不能太短, 太短不能满足各态历经假设[2], 并且会低估了通量值[3-4]; 另一方面该截断时间尺度也不能太长, 太长不能保证数据的平稳性。在实际计算中, 通常取30~60 min作为截断时间尺度[2], 但对于弱风、湍流较弱情况下, 由于中尺度运动(包括重力内波、下泄气流等)对通量计算的影响, 采用固定的30 min或更长的截断时间尺度会使我们采用涡相关法计算出的通量存在很大的分散性。文献[1]利用飞机在海面上的观测资料指出在中尺度运动显著或弱风状况下, 涡相关法计算的海气通量对截断时间尺度的选取会非常敏感。文献[3]利用森林站点的观测资料指出低频运动对涡通量计算的重要性, 文献[4]认为应该使用更长的截断时间尺度去计算表层通量。
关于海气通量计算的截断时间尺度究竟该取多长, 它与哪些因素有关, 它对海气界面通量有何影响, 是本文主要关注的问题。海气通量涡相关法计算中, 正确的时间尺度的选取可以获得真实可靠的海气通量数据, 也为进一步认识和了解上层海洋与大气之间的相互作用提供重要的科学依据。
1 方法
1.1 观测资料
2009年7月11日至2009年7月25日, 作者在大连獐子岛海域布放了一个高约14 m, 质量达1.4 t的浮标, 该浮标主要由4部分组成:上桅杆、浮标主体、下桅杆和电池仓。该浮标的上桅杆上架装了 4层气象观测仪器:海面以上2.5 m左右为超声风速仪81000V和浮标运动传感器(Motion pack); 海面以上 4 m左右为超声风速仪HS50和开路CO2/H2O分析仪CS7500; 海面以上6 m左右为超声风速仪CSAT3和另一台开路CO2/H2O分析仪CS7500; 海面以上6.8 m为常规风速仪(Young 05103V)、温湿传感器(RT41382)和大气压力传感器(Pressure)。浮标主体上布放了5根波浪杆, 用于测量波浪信息。浮标下桅杆上还安装了3台仪器:海面以下 0.5 m和 1 m左右分别安装了一台水温仪TR-1050, 海面以下3 m左右安装了CTD。浮标的电池仓为整个观测系统提供电力支持。超声风速仪、两台开路CO2/H2O分析仪、运动传感器和波浪杆的采样频率为10 Hz, 常规观测仪器如Young 05103V、RT41382 和 Pressure每分钟观测一次, 2台水温仪TR-1050和CTD的采样频率分别为1 Hz和3 Hz。浮标布放海域的平均水深约为 35 m, 观测期间风速变化范围为0.5~17.3 m/s。大气温度一直高于海水温度且海面湿度偏高, 大气和海面的平均气温分别为23.12℃和19.25℃, 平均相对湿度为91%。
1.2 资料预处理
首先参考Vickers等[5]提到的野点去除方法对观测数据进行野点去除, 然后对观测数据进行晃动校正, 剔除浮标晃动对超声风速仪观测风速的影响,方法见文献[6]。
1.3 平均时间尺度研究方法
1.3.1 截断时间尺度和通量平均时间尺度的定义
为了说明通量计算过程中的平均时间尺度问题,我们首先采用文献[1]中的方法定义两个平均时间尺度, 即截断时间尺度T和通量平均时间尺度λ。
任意时刻t的垂向瞬时通量w′′φ, 在一段时间λ内求平均值, λ被定义为通量平均时间尺度。为了严格地满足雷诺平均法则,T与λ应该相等, 且T应采用无重叠窗口进行计算。然而, 有时为了获得大尺度的通量或更广泛的通量采样, 常常选取λ>T。
本研究中, 我们主要讨论截断时间尺度T对海气通量计算的影响。本文中, λ包含215个数据点, 约54 min。
1.3.2 多尺度分解法
我们使用多尺度分解法对海气通量涡相关法计算中的时间尺度问题进行分析。多尺度分解法是一种将信号分解成不同尺度的方法[7]。近年来, Vichers等[8]和Acevedo等[9]将该方法用于确定稳定边界条件下通量的湍尺度。下面我们以感热通量为例来介绍如何应用多尺度分解法确定截断时间尺度T。首先将温度和垂向速度时间序列(每个时间序列包含 2M个数据点,M=15)分成一系列的窗口, 这些窗口包含 1,2, 4, …, 2M个连续数据点。根据Vicker等[10], 窗口长度为2m(m<M)所对应的协谱值为:


通量的截断时间尺度T通过计算曲线Dwθ的跨零点或拐点获得。海气通量交换尺度可以从微尺度(湍流)到中尺度和更大的时间尺度(低频)。高频和低频(湍流和中尺度气流)可以通过能谱或协谱的谱隙区分开来[11]。采用多精度分解法可以找到谱隙, 进而确定截断时间尺度T。作为例子, 图1给出了顺风向动量通量Mu和感热通量Hs的多尺度协谱曲线和多尺度协谱累积曲线S(p), 可见在51.2 ~204.8 s之间的时间尺度上, 累积的顺风向动量通量和感热通量变化都很小, 则可以将这段缺少通量变化的时间尺度范围定为谱隙, 取该谱隙内的任一时间尺度计算通量都不会对相应的通量结果产生大的影响。这里我们取谱隙范围内曲线Dwθ的纵坐标值第一个与 0最接近或第一个改变符号的点所对应的时间尺度T作为截断时间尺度, 因此, 对于该时段数据我们取截断时间尺度T为102.4 s。

图1 Mu和Hs的多尺度协谱曲线和多尺度协谱累积曲线Fig. 1 Multiresolution cospectrum curve and multiresolution cospectrum accumulative curve for Mu and Hs
2 结果与分析
我们这里使用超声风速仪CSAT3的观测数据进行分析, 用于分析的每个时间序列都通过了数据质量控制, 其包含215个数据点, 约54 min。在进行多尺度分解前, 我们首先对风速数据进行三维坐标旋转, 旋转结果是和为0[12]。每隔30 min分析一个时间序列, 并获得一个截断时间尺度T, 最后一共得到 667组数据, 我们这里主要是分析动量通量和感热通量的时间尺度问题。
2.1 截断时间尺度与湍流强度之间的关系
[13], 我们使用湍流垂向速度的标准偏差σw来代表湍流强度, 而不用u*, 这是因为中尺度交换对u*的影响很大, 对σw的影响较小。从图2可以看出, 截断时间尺度依赖于湍流强度和水平风速。当湍流强度增加或风速增大时, 动量通量和感热通量的截断时间尺度也会逐渐增加, 且在整个观测资料范围内,感热通量的截断时间尺度要大于动量通量的截断时间尺度。图3给出了动量通量和感热通量在不同湍流强度范围内各自截断时间尺度的分布频率情况, 可以看出, 截断时间尺度成不对称分布; 当湍流强度比较弱时(σw<0.3 m/s), 截断时间尺度主要分布在100 s左右;当湍流强度比较强时(σw>0.3 m/s), 截断时间尺度主要分布在800 s左右。本文中得到的截断时间尺度小于陆地上通常使用的30 min。

图2 T随σw和U的变化Fig. 2 T as a function of σw and U
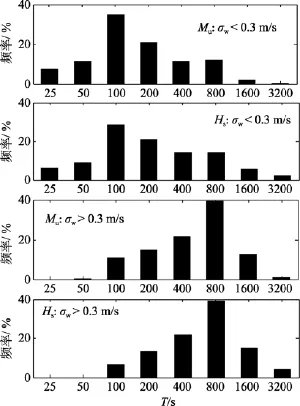
图3 T的频率分布图Fig. 3 Frequency distributions of T for Mu and Hs
2.2 截断时间尺度对海气通量计算结果的影响
我们将应用多尺度分解法获得的T计算出来的海气通量称之为湍通量, 应用约54 min的固定时间尺度计算出的海气通量称之为总通量。图4、图5直观地给出了两种截断时间尺度计算出的海气通量值,Mv代表侧风向动量通量。可以看出, 当σw<0.3 m/s时, 多尺度分解法计算的海气通量变化较平缓, 而固定时间长度计算出的海气通量变化比较剧烈, 两者画出的曲线差别较大, 这是因为弱湍流下, 两种截断时间尺度相差较大(一个约 100 s, 另一个约3 200 s), 大的固定时间尺度很容易使我们计算的通量受到中尺度运动的影响[10,14], 而由于我们对中尺度运动采样的不完整, 造成使用固定时间尺度计算出的通量值失真; 当σw>0.3 m/s时, 两种时间尺度计算出的海气通量曲线比较接近, 变化相对一致,这是因为此时两种截断时间尺度相差较小些(一个约800 s, 另一个约3 200 s)。

图4 湍流强度小于0.3 m/s时应用多精度分解法和固定时间长度计算出的湍通量和总通量Fig. 4 The turbulent flux calculated by the cutoff time scale and total flux calculated by fixed time scale when turbulence intensity is less than 0.3 m/s

图5 湍流强度大于0.3 m/s时应用多精度分解法和固定时间长度计算出的湍通量和总通量Fig. 5 The turbulent flux calculated by the cutoff time scale and total flux calculated by fixed time scale when turbulence intensity is more than 0.3 m/s
为了进一步说明T对海气通量计算的影响, 我们计算了不同湍流强度范围内感热通量的平均值及其标准偏差(见表1)。可以得到, 当σw<0.3m/s时, 两种截断时间尺度计算出的感热通量的平均值从-6.99 W/m2变成-9.13 W/m2, 变化了30.7%({[-6.99-(-9.13)]/( -6.99)}×100%), 重要的是通量的不确定性(这里我们采用 Campos等[13]关于通量不确定性的定义, 即:(通量标准偏差/通量平均值)×100%从98.3%变成 208.4%, 变化了 107.9%({[208.4%-98.3%]/98.3%}×100%), 说明弱湍流下, 截断时间尺度的选取对感热通量平均值的计算没有太大的影响,而主要是增加了通量计算的不确定性; 当σw>0.3 m/s时, 两种截断时间尺度计算出的感热通量的平均值从-25.30 W/m2变成-27.12 W/m2, 变化了7.2%, 而通量不确定性从76%变成93.1%, 变化了22.4%, 这也说明T的选取对感热通量平均值的影响要远小于对通量不确定性的影响; 另外通过对不同湍流范围内的计算结果比较发现,T的选取对感热通量计算的影响在强湍流下要小于弱湍流的情况。这些都与文献[13]应用陆地资料得到的结论类似。

表1 感热通量的平均值和标准偏差Tab. 1 The average value and standard deviation of sensible heat flux
3 结论
本文讨论分析了海气通量涡相关法计算中的时间尺度问题。Treviño等[15]指出, 只有在平稳和不相关情况下才能合理地找到湍流时间序列的平均值。Campos等[13]提出应用协谱谱隙确定的截断时间尺度作为湍通量时间尺度计算出的平均值、方差和协方差才是有意义的。因此本文首先采用多尺度分解法获得了计算湍通量的截断时间尺度, 然后讨论了该截断时间尺度的一些特征及对通量计算值的影响。截断时间尺度随着湍流强度或水平风速的增加而增加, 且感热通量的截断时间尺度均大于动量通量的截断时间尺度; 在弱湍流状态下, 动量通量和感热通量的截断时间尺度主要分布在100 s左右, 在湍流较强时, 动量通量和感热通量的截断时间尺度主要分布在800 s左右; 弱湍流状态下, 湍通量和总通量之间差别较大, 而在强湍流状态下, 湍通量和总通量之间差别较小; 通过计算感热通量的平均值和标准偏差得到截断时间尺度对感热通量平均值的影响较小, 但对感热通量不确定性有很大的影响,这两种影响之间的差别会随着湍流强度的增加而减小。本文只讨论了计算海气界面动量通量和感热通量中的时间尺度问题, 但文中提出的方法可同样应用于海气界面潜热通量和二氧化碳通量中时间尺度的确定和分析。
参考文献:
[1]Sun J, Howell J F, Esbensen S K, et al. Scale dependence of air-sea fluxes over the western equatorial pacific [J]. J Atmos Sci, 1996, 53(21):2997-3012.
[2]Kaimal J C, Finnigan J J. Atmospheric boundary layer flows [M]. UK:Oxford University Press, 1994:289.
[3]Sakai R K, Fitzjarrald D R, Moore K E, et al. Importance of low-frequency contributions to eddy fluxes observed over rough surfaces [J]. Journal of Applied Meteorology, 2001, 40:2178-2192.
[4]Finnigan J J, Clement R, Leuning R, et al. A re-evaluation of long-term flux measurement techniques PartⅠ:Averaging and coordinate rotation [J].Boundary Layer Meteorol, 2003, 107:1-48.
[5]Vickers D, Mahrt L. Quality control and flux sampling problems for tower and aircraft data [J]. J Atmos Oceanic Technol, 1997, 14:512-526.
[6]Miller S D, Hristov T S, Edson J B, et al. Platform motion effects on measurements of turbulence and air-sea exchange over the open ocean [J]. J Atmos Oceanic Technol, 2008, 25:1683-1694
[7]Howell J F, Mahrt L. Multiresolution flux decomposition [J]. Boundary Layer Meteorol, 1997, 83:117-137.
[8]Acevedo O C, Moraes O L L, Fitzjarrald D R, et al.Turbulent carbon dioxide in very stable conditions [J].Boundary Layer Meteorol, 2007, 125:49-61.
[9]Vickers D, Mahrt L. A solution for flux contamination by mesoscale motions with very weak turbulence [J].Boundary-Layer Meteorol, 2006, 118:431-447.
[10]Vickers D, Mahrt L. The Cospectral Gap and Turbulent Flux Calculations [J]. J Atmos Oceanic Tech, 2003, 20:660-672.
[11]Smedman A S, Ahogstrom U. Spectral gap in surface-layer measurements [J]. J Atmos Sci, 1975, 32:340-350.
[12]王金良, 宋金宝. 关于涡相关海气通量计算的资料处理技术[J]. 海洋科学, 2009, 33:1-5.
[13]Campos J G, Acevedo O C, Tota J, et al. On the temporal scale of the turbulent exchange of carbon dioxide and energy above a tropical rain forest in Amazonia [J].Journal of Geophysical Research, 2009,114:D08124.doi:10.1029/2008JD011240.
[14]Howell J F, Sun J. Surface-layer fluxes in stable conditions [J]. Boundary Layer Meteorol, 1999, 90:495-520.
[15]Treviño, G, Andreas E L. On the Reynolds averaging of turbulence time series [J]. Boundary Layer Meteorol,2008, 128:303-311.
On the average time scale used in the calculations of the air-sea fluxes by eddy covariance method
HUANG Yan-song1,2, SONG Jin-bao1, FAN Cong-hui1
(1. Key Laboratory of Ocean Circulation and Waves, Institute of oceanology, the Chinese Academy of Sciences,Qingdao 266071, China; 2. Graduate University of the Chinese Academy of Sciences, Beijing 100039, China)
Dec., 6, 2010
average time scale; air-sea fluxes; spectral gap; multiresolution decomposition; cutoff time scale
Based on data collected at a moored buoy located in the Yellow Sea for a period of 14 days, the cutoff time scale (CTS), a parameter in the calculations of the air-sea fluxes by the eddy covariance method was determined by the multiresolution decomposition method, and could be used in separating turbulent fluxes and mesoscale fluxes from the total air-sea fluxes. The CTS increased with the crease of turbulence intensity or wind velocity.The CTS of the sensible heat flux was always longer than that of the momentum flux. When the turbulence intensity was less than 0.3 m/s, most of CTS of the momentum and sensible heat fluxes were around 100 s and the difference between the turbulent and total fluxes was large; when the turbulence intensity is larger than 0.3 m/s,most of CTSs were around 800 s and the turbulent fluxwas similar to that of total fluxes. The calculation and analysis of the average and uncertainty of sensible heat flux indicated the CTS has more influence on the average value than on the uncertainty of the flux and such a difference became smaller as the turbulence intensity increases. The choice of CTS is important to get the air-sea fluxes, providing a scientific basis for further understanding the interaction between the ocean and atmosphere.
P731; P732 文献标识码:A 文章编号:1000-3096(2011)11-0114-06
2010-12-06;
2011-09-29
国家重点基础研究发展计划(2011CB403501); 国家自然科学基金(40876012); 国家基金委创新群体项目(40821004)
黄艳松(1983-), 女, 河北秦皇岛人, 博士研究生, 研究方向:物理海洋学, E-mail:huangyansong.student@sina.com; 宋金宝,通信作者, 电话:0532-82898506; E-mail:songjb@qdio.ac.cn
刘珊珊)

