汇率与股票资产价格泡沫关系的实证分析及货币政策研究
逯宇铎, 王 昱
(大连理工大学 经济系,辽宁 大连 116024)
汇率与股票资产价格泡沫关系的实证分析及货币政策研究
逯宇铎, 王 昱
(大连理工大学 经济系,辽宁 大连 116024)
文章首先分析了人民币汇率和我国股票资产价格(以上证A股为例)的现状,然后就人民币汇率升值和上证A股股价变化关系进行了实证研究,其中包含了金融危机的影响。实证结果表明,从长期来看本币升值将导致股票资产价格泡沫下降;接着通过建立应对汇率升值导致的股票资产价格泡沫的货币政策模型得出,当出现资产价格泡沫时,多数情况下应实行紧缩货币政策,以免资产价格泡沫在短期趋于过大,减轻资产价格泡沫经长期后破灭产生通货紧缩等更大的不利影响。
汇率升值;股票资产价格;泡沫;货币政策
一、人民币汇率与股票资产价格的现状分析
1.人民币汇率变化
从2005年7月21日起,我国开始实行以市场供求为基础、参考一篮子货币进行调节、有管理的浮动汇率制度。我国的汇率制度终于做出了历史性的变革。经历4年的时间,人民币兑美元的月平均汇率数值已经从2005年7月的8.24∶1上升至2009年8月的6.83∶1,升值幅度达到17.5%。
我国推进人民币汇率形成机制改革的目标主要是希望能够通过汇率改革来缓解对外贸易不平衡、扩大内需以及提升企业国际竞争力、提高对外开放的水平。然而在这样的主观意愿之下,却也相伴造成了国际资本的大量流入以及国内资产价格的大幅攀升。
2.上证A股股价的变化
中国股票市场的上证A股指数在2005年6月的最低点1 047.65点开始上涨,至2007年10月,A股指数达到6 429.68的高点,2年时间的涨幅约为5倍多。在此期间,其涨幅远远超过其实体企业的经济增长速度。可以说,该市场中股票资产价格存在较为严重的泡沫成分。
自中国A股市场在2007年10月达到最高峰之后并没有持续多久就开始掉头向下、一路狂跌,至2009年 1月底已经跌到 2 100点左右,跌幅超过67%.这表明股票价格存在非常大的波动性,而且其波动幅度远超过成熟资本市场。在此之后,由于美国金融危机后的救市政策以及对人民币的信心,股指又开始逐步回升,到2009年8月底达到3 651.2点。
二、人民币汇率升值与股票资产价格泡沫的实证研究
1.数据的选取及稳定性检验
本文建立计量模型时,选取汇率值与上证A股股指的时间范围为2002年1月~2009年8月,数据来源为中国人民银行。使用ADF单位根检验方法,结果如表1所示。
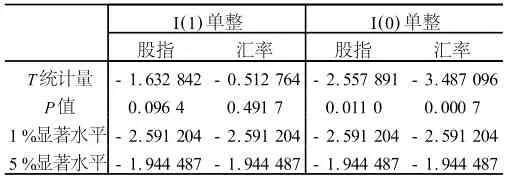
表1 数据平稳性检验
ADF单位根检验中不包含趋势项和常数项,滞后期根据AIC准则选定为2。由表1中数据可知,汇率和股指拒绝序列平稳的原假设,并在5%显著性水平下接受2项均为一阶单整的原假设,即汇率和股指为一阶单位根过程。这表示汇率和股指可以进行协整分析。
2.协整关系检验
本文首先建立股指和汇率间的关系模型,并且在此基础上引入代表金融危机的虚拟变量,通过OLS回归后对残差序列进行稳定性检验,从而判断两变量是否存在长期的协整关系。
本文用Et表示人民币对美元的直接报价,Pt表示上证A股月度最高股指,Dt表示金融危机,并建立变量间的模型:

通过OLS回归得到结果如表2所示。

表2 变量的OLS回归结果
通过D-W值我们可以判断序列存在正自相关性,并计算LM(2)=6.88,LM(3)=6.75,由此可以说明残差项存在二阶序列正相关,然后对模型进行修正。

经过OLS回归后得出结果如表3所示。

表3 修正的变量OLS回归结果
由表3可以看出,模型消除了序列自相关问题,然后对模型残差进行稳定性检验,结果如表4所示。

表4 残差稳定性检验
由表4可以看出,残差序列稳定,不存在单位根,从而说明模型存在长期稳定关系。从长期来看,当汇率值每下降0.01个单位,则股票指数减少约28.25,即人民币汇率每升值0.01个单位,股票指数下降约28.25。可见,从长期来看本币升值会促使股票资产价格泡沫大幅度下降。
3.误差修正模型ECM的建立
由于模型存在长期的协整关系,所以我们可以建立股指与汇率的短期误差修正模型:
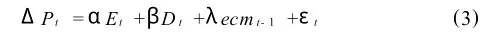
通过回归分析得到如下结果,如表5所示。
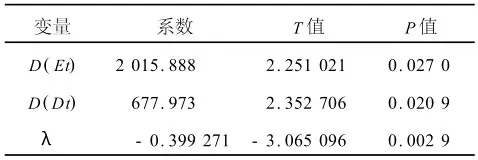
表5 误差修正模型的回归结果
4.格兰杰因果关系检验
上述回归模型只能说明二者的依存关系,本文的一个重要目标是要确定人民币汇率与股价指数的因果关系,这里采用格兰杰因果关系检验法对两个变量进行单向检验。
由于格兰杰检验对滞后期长度的变化比较敏感,因此根据AIC准则确定滞后期长度为4,计算结果如表6所示。
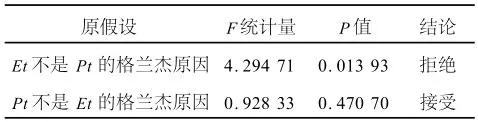
表6 变量的因果关系检验
从表6可以看出,在滞后期为4的情况下,人民币汇率的变动影响到股价指数,而股价指数的变动对人民币汇率的影响则很弱[1]。
三、应对汇率升值导致的股票资产价格泡沫的货币政策研究
通过实证分析表明,汇率升值在长期将导致股票资产价格大幅度下降,即资产价格泡沫破碎。为了避免这种长期资产价格大幅下降对经济体带来的不良影响,货币当局需要制定相应的货币政策用于提前应对这种汇率升值导致的股票资产价格泡沫在长期破碎后的问题。
在构建货币政策理论模型之前,我们需要明确,汇率与股价实际上是两种市场中的不同资产价格,前者对后者如果能发生传递影响,即一种资产价格变动后能够同时引起另一种资产价格发生变动,必然有中间变量进行传导。因此,本文在研究汇率升值对股票资产价格影响的宏观体系中引入中间变量。根据现代利率平价理论,即汇率的升贴水率等于本国和外国之间的利率差,所以本文选取利率为中间变量并作为汇率的替代变量。因此,货币当局可以通过利率的调整和变动来应对资产价格泡沫的破碎。
1.应对资产价格泡沫的理论模型构建
我们将建立一个简单的理论模型,用于应对上面讨论的问题,即基于人民币汇率的变动,进而作为中间变量的利率应该如何调整以应对非基于经济基本面的资产价格泡沫的上升和破碎造成的影响。
本文的理论模型中包含四个代表实际的关键因素:(1)资产价格的上升和下降对商品和服务价格通货膨胀的不对称的影响;(2)中央银行以控制通货膨胀为目标,并关注通货膨胀的波动以及其预期水平;(3)资产价格泡沫破碎的概率受到利率水平的影响;(4)假设资产价格泡沫破碎之后,它不会再重新形成。
模型主要研究上述变量之间的关系,进而为货币政策的实施做出铺垫。在模型中,我们还要假定经济体将运行三个时期,泡沫出现在第一个时期。在整个过程中,中央银行知道资产价格的上升并非基于经济基本面(虽然中央银行不一定一直清楚资产价格泡沫是否存在,但其可以判断出资产价格的变动是否脱离了经济基本面)[2]。
我们给出下面的模型:

其中,πt代表偏离中央银行目标值的通货膨胀的值,At代表资产价格偏离基本面的值,Rt代表利率水平,Dt为虚拟变量,如果资产价格泡沫破碎其值为1,反之为0。尽管模型中目标变量为通货膨胀,但如果目标变量为产出偏离其潜在的水平,下面的分析也同样适用。在这里我们暗含的假设为资产价格对通货膨胀的影响主要通过影响经济活动而产生。
我们假定资产价格At上升会对商品和服务价格产生上涨压力。At越大,这种直接影响会越大。然而,我们也假定,当泡沫破碎,资产价格返回到经济基本面时,不仅高资产价格的刺激效应会消失,而且还会产生紧缩效应。正如前文的讨论,这些效应对金融系统的稳定性产生了不利影响。资产价格越高,这种不对称的影响越大。
另一点需要注意的是,货币政策的实施存在滞后期。如果当前通货膨胀率高于目标水平,中央银行不能立刻使其恢复到目标水平。这表明中央银行必须通过预测未来以便设置当前利率。
当出现资产价格泡沫时,我们假设泡沫下一期返回到经济基本面值的概率为p,而它可以被认为是利率的函数。高利率增加了购买资产的成本,有可能使得商业周期缩短。这些变化增加了泡沫破碎的可能性。
下面我们定义当前利率和下期泡沫破碎概率的关系:

其中,利率Rt越大,利率对下期资产价格泡沫破碎的影响越大。如果泡沫破碎,下期就不会重新形成。如果泡沫没有破碎,它会以增长率g*进行增长。

其中,g=1+g*,资产价格泡沫的可能增长路径如图3所示。
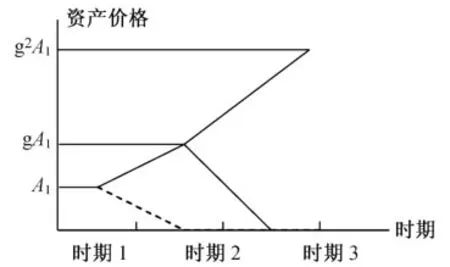
图3 资产价格泡沫的潜在路径
由图3我们可以观察到,泡沫出现在第1期,中央银行的任务就是使得预期通货膨胀的方差最小化。因为央行不能影响当前的通货膨胀率,所以就要使得下面的等式最小化:

其中,E表示预期值,下脚标表示时期。在时期2,目标函数将变为E2(π23)。这个目标函数表明中央银行不仅需要关注预期通货膨胀水平,还要关注其波动情况。
我们首先分析第2期可能存在的两个利率,一个是泡沫破碎下的利率,另一个是泡沫继续增长时的利率。使用这种方法我们计算出第1期中的最优利率水平,这就表示当中央银行设置第1期的利率时,它就能够改变第2期的利率水平,这依赖于泡沫是否破碎。
如果在上述问题中使用数学迭代,我们会引入非线性分析,这将使问题复杂化。所以为了简化分析,我们在问题的分析上使用参数设定的方法而非数学迭代的方法[3]。
在分析中我们设定α=1,β=2,第1期的泡沫A1的值为1。这样设定可以充分体现出资产价格变动给通货膨胀带来的不对称的影响。同时,我们还要设定g=2(即如果泡沫继续扩大,每一期它将扩大一倍)。通过使用上述三个参数,我们可以得出通货膨胀的三个可能路径,其中先假定利率为0。如果泡沫从第1期到第2期时破碎,那么通货膨胀在时期2将低于目标水平,在时期3又返回到目标水平上。然而,如果泡沫在时期2没有破碎,通货膨胀将超过目标水平。但重要的是,通货膨胀要么会大大高于目标水平,要么大大低于目标水平。

图4 利率为0条件下资产价格泡沫的潜在路径
在下面的分析中,我们设定泡沫破碎的外生概率φ=0.5。也就是说,如果利率为0,泡沫破碎的概率为0.5。分析结果总结在表7中。
首先假设利率的改变对泡沫是否破碎不产生影响(φ=0),如表7中的情况1a所示。在这种情况下最优政策就是保持利率不变。如果泡沫继续增长,通货膨胀将等于2;如果泡沫破碎则等于-2,对于给定的两种情况,他们发生的概率相同,即泡沫破碎的预期损失等于泡沫继续增长的预期损失。预期的通货膨胀在第2期和第3期都等于目标水平。在第1期时预测的第2期的通货膨胀方差为4,第3期为8,并且这些方差不能通过改变利率而减少。
在例子中,货币政策不能影响到泡沫破碎的概率,所以未来可能发生的事件不能影响当前货币政策的设定。当然,下期可能发生的事件也非常重要。如果我们增加泡沫的增长率,减少泡沫破碎的概率,或者减少与泡沫破碎相关的成本,此时利率就应该提高,而不是保持常数。
然后我们开始分析中央银行能够影响泡沫破碎的概率的情况,即φ不为0,不妨设φ=0.2,这种情况如表7中的1b所示。此时最优政策就是提高利率,如R=0.6。更高的利率增加了泡沫破碎的可能性,从0.5变为0.62,这项货币政策的影响导致预期通货膨胀在第2期低于目标水平(预期通货在第3期将返回到目标水平)。即使预期通货膨胀低于目标水平,但预期通货膨胀的方差会小于原来的第2期和第3期之和(此时
通过上述分析,我们可以总结出,货币政策对模型产生两种影响:标准的和非标准的影响。首先,如果中央银行将泡沫破碎的概率看作是固定的,它通常面临的问题是在面对不确定性下做出决定。央行通过分析第2期通货膨胀可能的水平来解决问题,然后考虑相关概率,计算出利率水平,使得预期通货膨胀的方差最小化。
其次,非标准的影响就是货币政策对泡沫破碎产生影响。如果央行能够影响泡沫破碎的概率,它就不仅需要考虑第2期的结果,还要考虑第3期的可能结果。尽管标准的传导滞后期为1期,但是货币政策也能够影响到随后时期中事件发生的概率。如果货币政策能够使第2期中资产价格泡沫破碎,在第3期泡沫破碎的概率就变为0。所以在这种情况下,中央银行有必要提高利率来增加资产价格在第2期破碎的概率,因此减小了在第3期中出现更极端结果的概率。
随着泡沫增长率的增加,最优利率也要随速率增加。较高的泡沫增长率增加了下一期可能出现结果的波动性,对第3期的影响更大。结果,在第2期中将泡沫破碎的益处变大。例如,如果泡沫增长率为3而非2(所以泡沫每期会增加3倍,而非2倍),此时,第1期的最优利率为2.1,泡沫破碎的概率增加到0.9(表7中的1c)。在某种意义上,利率的大幅度增加会对泡沫产生战略性打击。货币政策紧缩到一定程度将必定使泡沫破碎。政策制定者清楚这样做不仅会使经济增长因利率的滞后效应而放缓,而且会由于资产价格下降而产生不利影响,但是如果不提高利率会导致未来发生更大的冲击[4]。
在表7的情况1中,当泡沫破碎的概率为外生时,应保持利率水平不变,而概率为内生时,则应增加利率。现在我们来考虑表7中的情况2a,其中最优政策是当泡沫破碎概率为外生时提高利率水平。在这种情况中,泡沫破碎的外生概率由0.5减少到0.2,并且保持其他参数不变。由于下期泡沫破碎的概率减少,在第2期通货膨胀有可能高于目标水平,所以第1期的最优利率水平应该提高(从0增加到1.2)。如果现在我们设定概率为内生的,则最优货币政策为提高利率(情况2b中R= 1.0),但是利率低于情况2a中的利率水平。
在这个例子中,用于抵消资产价格泡沫扩张效应的高利率同时增加了泡沫破碎的概率,这就放大了紧缩货币政策的预期效果,所以利率水平就可以比情况2a中低。得到这种结果的部分原因是由于我们模型的设定形式。如果泡沫破碎的概率并非利率水平的函数,而是利率与抵消标准的预期通货膨胀所需要的利率水平之差的函数(如2a中的1.2),将会建议实施比标准分析更紧缩的货币政策。
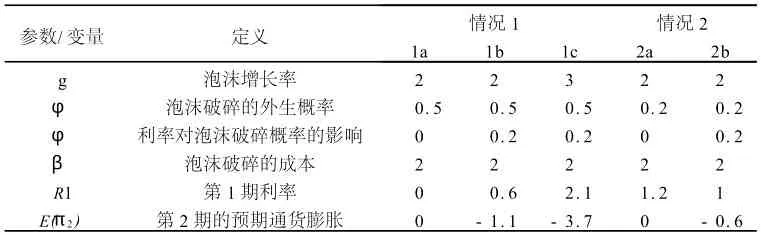
表7 模型分析结果
尽管上述分析结果是基于我们设定好的参数值进行分析的,但对模型的分析是具有一般性的,并且对于更广泛的参数值的设定依然成立。基本思想就是央行需要提高利率打破资产价格泡沫,使得预期通货膨胀在短期低于目标水平。这个结论由三个基本要素推导出来:(1)泡沫破碎的概率是利率的增函数;(2)如果泡沫破碎,它将不会再次形成;(3)央行希望避免通货膨胀偏离目标水平过大[5]。这个结果对于一系列的参数值都成立,只要泡沫破碎的直接效应α和泡沫破碎的间接非对称效应β不为0。
2.应对资产价格泡沫的理论模型扩展
在前文的分析中,我们假定下期泡沫破碎的概率仅是当前利率的函数。这里我们将引入泡沫的大小At作为影响下期泡沫破碎概率的变量。我们假定泡沫At越大,下期泡沫破碎的概率越大。这个假设会随着泡沫的变大而得到证明,此时多数人会认为资产价格的上升形成了泡沫,并且开始不希望购买这种资产。
根据上述分析,我们重新定义等式:
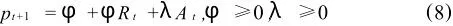
类似地,模型分析结果如表8所示。此时我们依然设定泡沫增长率为2,泡沫破碎的外生概率为0.5,利率对泡沫破碎的影响为0.2(表8中1b的情况,λ=0)。首先,我们假定λ=0.15(如表8中3a所示)。由于泡沫破碎的概率受到了资产价格泡沫水平的影响,所以最优利率就减少了。在这个例子中,第1期的最优利率为0.3,而非0.6。如果增大泡沫水平对泡沫破碎概率的影响,利率将会减小为负(情况3b)。由此我们可以发现这样一个规律,如果泡沫是否破碎受到其自身影响越大,货币政策就会变得越弱。如果泡沫因为其自身影响而破碎的可能性变得很大时,货币政策需要关注的则是泡沫破碎引起的紧缩影响。所以在这种情况下,反而要求央行在泡沫即将破碎前预防性地适当减少当期利率水平,以便用于缓冲资产价格泡沫因自身影响而破碎后引起的通货紧缩等不良影响。

表8 扩展模型分析结果
四、结 论
本文构建了一个理论框架用于分析货币政策应该如何应对资产价格泡沫。得出的主要结论是,当出现资产价格泡沫时,在多数情况下应实行紧缩货币政策,以避免资产价格泡沫短期内趋于过大。原因在于这项货币政策可以缓解资产价格泡沫经长期后破灭对经济体产生的更为严重的通货紧缩等极端不良影响。但当资产价格泡沫破碎的可能性受到其自身的影响程度大大超过利率水平的影响时,货币当局则需要在泡沫破碎前预防性地适当减少利率水平,用以缓冲泡沫破碎后的不良影响。这个结论由三个基本要素所支持:(1)紧缩的货币政策增加了泡沫破碎的可能性;(2)当泡沫破碎后短期将不会重新形成;(3)货币当局要尽力避免通货膨胀的极端影响。
金融机构要抑制股票市场等资产市场的过度投机,降低国际游资的短期投机收益预期。与人民币预期升值率的变化相比,“利差”的变动对短期国际资本流动的影响力要小得多。因此,国内的利率政策可用于抑制汇率升值背景下的投资过热和信贷过快增长,而不用太担心提高利率会对短期国际资本流动产生大的影响。要真正抑制短期国际资本的流入投机于股票等资本市场,必须有效应对人民币汇率升值预期,以寻求治理内外部失衡的政策组合来有效应对。
[1]蔡文洁.人民币升值对中国资产价格的影响研究[J].当代经济研究,2009,4(2):81-88.
[2]刘建江,徐长生.本币升值影响通货紧缩的机理[J].当代经济研究,2005,6(1):39-44.
[3]罗雪松.人民币汇率升值与资产价格泡沫关系研究[J].统计与决策,2009,5(4):41-48.
[4]黄飞雪,侯铁珊.人民币升值对大连与沈阳上市公司股价的弹性比较[J].大连理工大学学报(社会科学版),2009, 30(1):62-67.
[5]GRUEN D,PLUMB M,STONE A.How should money policy respond to asset-price bubbles[J].Social Science Research Network electronic library,2007,(8):90-97.
Empirical Analysis of the Relationship between Exchange Rate and Stock Asset Price Bubbles and Money Policy Research
LU Yu-duo, WANG Yu
(School of Economics,Dalian University of Technology,Dalian 116024,China)
The paper first analyzes the current situation of exchange rate and stock asset price in China(taking SSE A Share for example),and then conducts an empirical study of the relationship between RMB exchange rate appreciation and changes in SSE A Share price including the influence of the financial crisis.The result shows that exchange rate appreciation will cause the fall in stock asset price in the long-term.By developing a money policy model which serves to respond to the stock asset price bubbles caused by exchange rate appreciation,it is concluded that upon the occurrence of asset price bubbles,tightened monetary policy should be implemented in most cases to avoid larger bubbles in the short-term and the worse effects such as deflation after the long-time burst of the asset price bubbles.
exchange rate appreciation;stock asset price;bubbles;money policy
F830.9
A
1008-407X(2011)01-0025-06
2010-02-16;
2010-09-29
国家社会科学基金项目(10CJL039)
逯宇铎(1956-),男,辽宁大连人,教授,博士生导师,主要从事国际贸易、产业跨国研究;王昱(1984-),男,辽宁大连人,大连理工大学经济系硕士研究生,研究方向为国际贸易。

