基于Visual C++的电子光栅衍射模拟

祝智浩，李士本

(温州大学物理与电子信息工程学院，浙江温州 325035)

基于Visual C++的电子光栅衍射模拟

祝智浩，李士本†

(温州大学物理与电子信息工程学院，浙江温州 325035)

根据光栅衍射的强度分布函数和德布罗意物质波理论，在Visual C++的环境下采用蒙特卡罗舍选法对大量电子进行舍选，从而对电子光栅衍射进行模拟．该模拟形象、直观，有助于学生理解电子的波粒二象性和概率波的概念．

电子；光栅衍射；Visual C++；模拟

在光学发展史上，关于光的本性有两种完全对立的学说，一种是波动说，一种是微粒说，这两种学说，在历史上争论了很长时间，直到爱因斯坦的光量子学说提出，确立了光的波粒二象性，多年来关于光本性的争论才得以整合[1]．法国科学家德布罗意又进一步发展了光的波粒二象性理论，认为实物粒子也具有波粒二象性，粒子在运动过程中其内禀属性（如质量、电荷等）保持粒子性，运动行为则呈波动性[2]．

随着计算机模拟技术的发展，在实验教学中可以利用编程方法对电子的双缝衍射实验进行模拟[3-4]．笔者在Visual C++环境下，对更一般的情况——光栅衍射（双缝衍射为光栅N=2的特殊情况）进行模拟，该模拟形象、直观，有助于学生理解实物粒子的波粒二象性和量子力学中几率波的概念[5]．

1 光栅衍射原理

质量为m的电子束，通过加速电压U后，穿过光栅常量为d、光栅缝数为N、各缝宽为b的光栅，在距离为D的屏上产生衍射条纹，如图1所示．

根据德布罗意关系，在忽略相对论效应的条件下（vc）,可以得到波长关系：

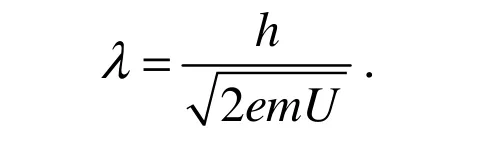
光栅衍射的强度分布函数[6]为：

图1 光栅衍射示意图

2 Visual C++模拟程序

首先利用Visual C++编程，让计算机产生一组随机点(x,y)，这些点的(x,y)对应窗口中的点的坐标，然后采用蒙特卡罗舍选抽样法[7]对产生的随机点进行筛选输出，即再生成一组均匀分布的、取值在0 – 1之间的随机数l，将l与先前随机产生的x所对应的强度分布函数K(x)进行比较，当K(x)>l时，输出该点(x,y)，否则不输出，直到所有产生的点即所有的电子都打完为止．此外，设置延时程序，每打出10个电子就刷新窗体（UpdateWindow()函数），以便可以动态演示电子光栅衍射图像的形成过程．窗口最终设计如图2所示．源代码主体部分如下：

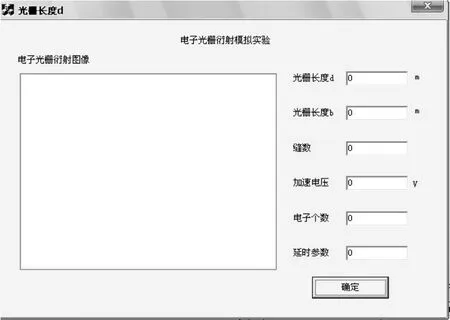
图2 电子光栅衍射窗体设计

3 不同参数下的运行结果

3.1 不同缝数下电子光栅衍射模拟

光栅常数设置如下：d= 6.0 × 10-7m，b= 1.0 × 10-7m，加速电压U= 500 V，电子个数100 000，延时参数1000，缝数N分别为2、5、10、20．实验结果如图3所示．

图3 不同缝数下光栅衍射图像

从实验结果可知，零级条纹处最黑，电子在该处出现的概率最大，随着级数的增加，逐级递减；条纹随着光栅缝数N的增大由粗变窄，在一定区域内能够观察到的条纹级数增多．

3.2不同电子数下电子光栅衍射模拟

光栅缝数N设置为5，电子个数分别为1 000、4 000、40 000、80 000，其余参数和上述实验一致．实验结果如图4所示．

图4 不同电子数下光栅衍射图像

从实验结果可知，当电子数目较少时，波函数的统计效应不明显，光栅衍射特征不明显，主要表现为电子的粒子性；随着电子数目的增多，波函数的统计效应越来越大，光栅衍射特征逐渐明显，这时主要表现为电子的波动性．

4 结 语

本文利用Visual C++模拟电子光栅的衍射行为，得到在不同缝数和不同电子数下电子光栅的动态衍射图像，形象地说明了实物粒子的波粒二象性．此外，还可以通过改变加速电压、光栅常数等来研究参数对光栅衍射图像的影响．在教学中利用该程序模拟电子光栅衍射实验，既可以减少实验设备的投入，又能引起学生的学习兴趣，有利于学生学习效率的提高．

[1] 曹天元. 量子物理史话上帝掷骰子吗[M]. 沈阳: 辽宁教育出版社, 2008: 8-104.

[2] 张哲华 刘莲军. 量子力学与原子物理学[M]. 武汉: 武汉大学出版社, 2004: 86-87.

[3] 李端明. 电子双缝衍射的计算机模拟[J]. 大学物理, 2008, 27(11): 53-55.

[4] 罗礼进. 基于蒙特卡罗的电子双缝衍射的计算机模拟[J]. 南通大学学报, 2005, 12(4): 62-64.

[5] 曾谨言. 量子力学导论[M]. 北京: 北京大学出版社, 2009: 17-87.

[6] 姚启军. 光学教程[M]. 1版. 北京: 高等教育出版社, 2008: 110-111.

[7] 马文淦. 计算物理学[M]. 合肥: 中国科学技术大学出版社, 2001: 19-123.

Visual C++-based Simulation of Electron Diffraction Grating

ZHU Zhihao, LI Shiben
(College of Physics and Electronic Information Engineering, Wenzhou University, Wenzhou, China 325035)

According to the intensity distribution function of diffraction grating and the theory of De Broglie wave, electrons were selected by means of Monte Carlo’s acceptance-rejection method to simulate Visual C++-based electron diffraction grating. The simulation is vivid, intuitive and helpful to understand the wave-particle duality and the concept of probability wave for students.

Electron; Diffraction Grating; Visual C++; Simulation

(编辑：王一芳)

O439

A

1674-3563(2011)05-0027-05

10.3875/j.issn.1674-3563.2011.05.005 本文的PDF文件可以从xuebao.wzu.edu.cn获得

2010-10-26

祝智浩(1988- )，男，浙江绍兴人，研究方向：应用光学．† 通讯作者，shibenli@wzu.edu.cn