＊ Banach空间二阶积分边值问题的正解

丁永宏

(西北师范大学数学与信息科学学院,甘肃兰州 730070)

＊Banach空间二阶积分边值问题的正解

丁永宏

(西北师范大学数学与信息科学学院,甘肃兰州 730070)

讨论了Banach空间二阶边值问题

正解的存在性与多重性.通过对非紧性测度的计算,利用严格集压缩映射的不动点理论,给出了该问题正解存在与多个正解存在的充分条件.

存在性;正解;非紧性测度;不动点;Banach空间

0 引言

设E为Banach空间,P⊂E为正规锥,正规常数为1,P导出E中的半序≤.考虑二阶积分边值问题

正解的存在性,其中f∈C[I×P,P],I=[0,1],g,h∈L1[0,1]为非负函数,a≥0,b≥0,c≥0,d≥0,ρ=ac+ad+bc＞0.

对于该问题,当E=R1时,已有学者做过研究,见文献[4-5],然而在抽象空间,结论尚不多见.由于有限维空间与无限维空间的本质差异,在无限维空间中,非线性项f(t,u)的连续性保证不了解的存在性,因此,还要对f加上一定的条件.在文献[1,3]中,作者假定f一致连续,且满足非紧性测度条件,分别讨论了Dirichlet边值问题与Sturm-Liouville边值问题正解的存在性.而本文通过对非紧性测度的精细计算,将文献[1,3]中对f一致连续这个很强的条件减弱为连续,运用严格集压缩映射的不动点理论,获得了问题(1)正解的存在性与多重性结果.

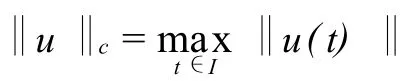
下面给出一些文中用到的定义和引理:

定义0.1[11]设P为实Banach空间E中的锥,P＊={ψ∈E＊:ψ(x)≥0,∀x∈P},称P＊为P的共轭锥.

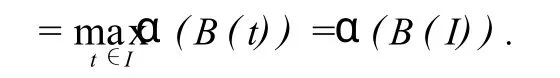
引理0.2[10]设E为Banach空间,D⊂E有界,则存在D的可数子集D0,使得α(D)≤2α(D0).

引理0.3[2]设E为Banach空间,B={un}⊂C[I,E],若存在g(t)∈L1(I),使得‖un(t)‖≤g(t),a.e.t∈I,n=1,2,…,则α(B(t))∈L1(I),且有

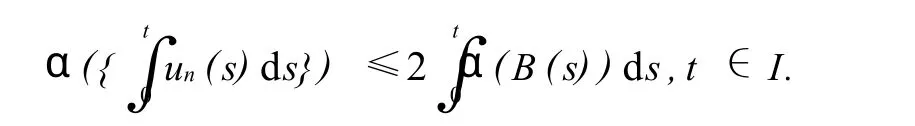
特别当B有界时,上式成立.

引理0.4[9]设P为实Banach空间E中的锥,Pr,s={x∈P∶r≤‖x‖≤s},其中s＞r＞0,A:Pr,s→P是严格集压缩映射.如果A满足下列两条件之一.

(i)A x≤/x,∀x∈P,‖x‖=r,A x≥/x,∀x∈P,‖x‖=s,

(ii)A x≥/x,∀x∈P,‖x‖=r,A x≤/x,∀x∈P,‖x‖=s,

则A在P上有不动点x,满足r＜‖x‖＜s.

1 预备工作

为方便起见,记

我们假设

(H1)H,G∈[0,1),CKD F∈[0,1),

Tl,有α(f(I,D))≤Lα(D),其中Tl={x∈E∶‖x‖≤l}.

引理1.1[7]假设条件(H1)成立,则对∀y∈C[I,P],边值问题

综上,γ(t,s)≥z(t)γ(τ,s),∀t,τ,s∈I.

引理1.3 假设条件(H1)成立,则G(t,s)≤G(t,t)≤N,γ(t,s)≤M G(t,t)≤M N.

引理1.5 假设条件(H1),(H2)成立,Kr,R={u∈K∶r≤‖u‖c≤R},其中R＞r＞0,则A∶Kr,R→K为严格k-集压缩映射.

证明 设B⊂Kr,R,由引理0.2知,存在B的可数子集B0={un}使得

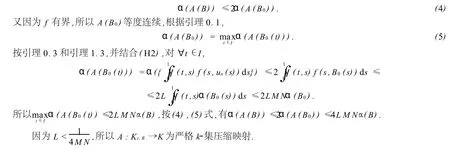
2 结论

[1] Guo D,Lakshmikantham V.Multiple Solutions of Two-point Boundary Value Problems of Ordinary Differential Equations in Banach Spaces[J].J M ath A na l A pp l,1998,129:211-222.

[2] Heinz H R.On the Behaviour of Noncompactness with Respect to Differention and Integration of Vecto r Valued Functions[J].N on linear Ana lysis,1983,7:1351-1371.

[3] Lou Ben-dong.Solutions of Superlinear Sturm-Liouville Problems in Banach Spaces[J].J Math Anal A pp l,1996,201:169-179.

[4] Yang Z.Positive Solutions of a Second Order Integral Boundary Value Problem[J].J Math Anal Appl,2006,321:751-765.

[5] Abdelkader Boucherif.Second-order Boundary Value Problems with Integral Boundary Conditions[J].N on linear Analysis,2009,70:364-371.

[6] Liu Bing.Positive Solutions of Generalized Sturm-Liouville Fou-point Boundary Value Problem in Banach Spaces[J].Nonlinear A na lysis,2007,66:1661-1674.

[7] Kang Ping,Wei Zhong-li,Xu Juan-juan.Positive Solutions to Fouth-order Boundary Value Problem sw ith Integral Boundary Conditions in Banach Spaces[J].A pp l M ath Com put,2008,206:245-256.

[8] Guo D,Lakshmikantham V.Nonlinear Problem s in Abstract Cones[M].San Diego:Academic Press,1988.

[9] Guo D.Lakshmikantham V,Liu X.Nonlinear Integral Equations in Abstract Spaces[M].Do rdrecht:Kluwer Academic Publishers,1996.

[10] 李永祥.抽象半线性发展方程初值问题解的存在性[J].数学学报,2005,48:1089-1094.

[11] 郭大钧,孙经先.抽象空间常微分方程[M].济南:山东科学技术出版社,1989.

Positive Solutions of Second Order Boundary Value Problem with Integral Boundary Conditions in Banach Spaces

DING Yong-hong
(College of Mathematics and Information Science,Northwest Normal University,Lanzhou730070,China)

The existence and multiplicity of positive solutions for second order boundary value problem

are discussed.The existence and multiplicity results by using the fixed-point index theory of strict set contraction operator and doing computation of measure of noncompactness was got.

existence;positive solution;measure of noncompactness;fixed-point;Banach spaces

O175.7

A

0253-2395(2011)01-0036-06＊

2010-04-06;

2010-06-02

甘肃省自然科学基金(0710RJZA 103)

丁永宏(1985-),男,甘肃天水人,硕士研究生,主要研究方向为非线性泛函分析.E-mail:dyh198510@126.com