沉积环境判别与分类的Bayes判别分析法

董文娟,朱远鑫,万明刚,吕一兵

(长江大学信息与数学学院,湖北荆州 434023)

0 引 言

沉积物粒度参数的变化受搬运介质、搬运方式、沉积环境和气候等因素控制,不同粒度组分的形成与搬运与沉积环境密切相关,处理、分析粒度数据可以进一步确定沉积环境,这对现代沉积学的研究,乃至古代沉积物的沉积环境分析无疑都具有重要的理论和现实意义.

在相关研究中,Sahu等[1]在对不同成因的样品进行分析研究的基础上,得到了各类沉积环境间的判别函数,曲政[2]给出了一种单样品粒度分布表征的方法.薛清太[3]通过测试分析发现沉积岩粒度中值分布、泥质含量、分选性等是影响油藏岩石渗透能力的重要因素,而正态分布和Φ正态分布能较好地描述低渗透砂岩油藏中沉积物的粒度分布特征,杨锐等[4]根据数理统计方法对粒度参数进行无偏估计,使之较以往参数估计更加符合无系统误差的评选标准,并利用这一方法对长乐东部海岸的风沙进行了系统的粒度参数分析,张平等[5]对典型稳定湖相沉积物和典型风成黄土粒度参数做了定量化分析,然后利用多元判别分析的Fisher准则建立了湖相与风成沉积物两种沉积相的判别函数.在上述研究的基础上,本文将判别分析理论应用于沉积环境的综合评判中,建立沉积环境判别与分类的Bayes判别分析模型,选用粒度的平均粒径、标准偏差、偏差、峰值4个指标作为判别因子,结合多元统计分析建立沉积环境判别与分类的Bayes判别函数.研究表明,所建立的Bayes判别函数可较理想地应用于沉积环境的判别与分类中,同时,将其应用于实际工程中取得了较为理想的效果.

1 Bayes判别分析

1.1 判别分析的基本思想

已知有 g个p维总体G1,G2,…,Gg,每个总体Gi可以认为是属于 Gi的指标,X= (X1,X2,…, Xp)T,取值的全体,它们分别具有互不相同的p维概率密度函数,f1(x),f2(x),…,fg(x),对于任一给定的新样品关于指标 X的观测值,x=(x1,x2,…, xp)T,关键是要判断该样品属于 g个总体中的哪一个.因而,判别分析是根据所研究个体的某些指标的观察值来推断该个体所属类型的一种统计学方法.在这些判别方法中,Bayes判别是使误判的平均损失达到最小的一种判别分析方法.

1.2 Bayes判别函数

设2个p维正态分布总体G1,G2,其概率密度函数为,

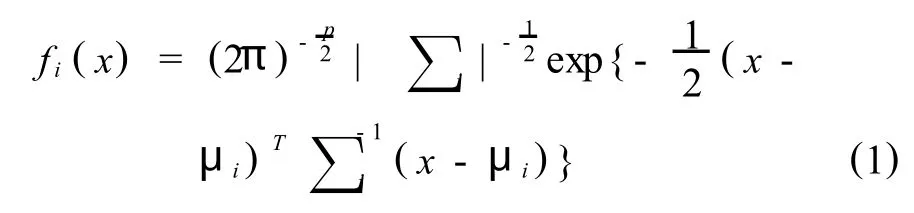
式中,μi,∑i为两总体的均值向量和协方差矩阵, |∑i|为∑i的行列式,i=1,2.

假设,∑1=∑2=∑,根据马氏(Mahalano-bis)距离和判别函数的概念可得,

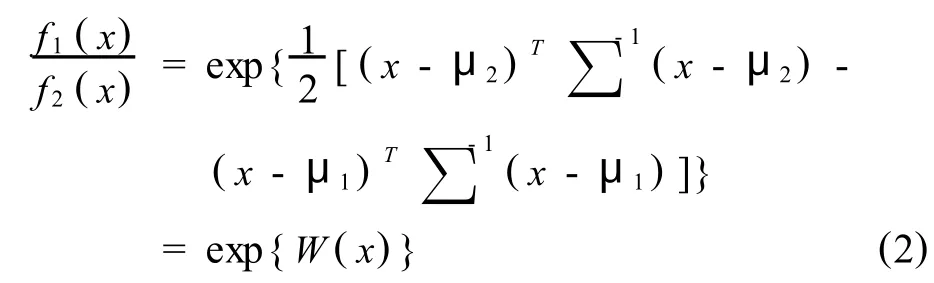
式中,

称为Bayes判别函数.

1.3 多正态总体的Bayes判别

现将式(3)推广到多正态总体的情形.设有 g个p维总体G1,G2,…,Gg,其概率密度函数如式(1)所示,此时,i=1,2,…,g.假设各正态总体的协方差矩阵相等,即,∑1=∑2=…=∑g=∑,则其Bayes判别函数为,

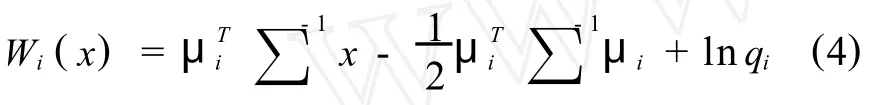
实际应用中,若μi,∑i未知,可以训练样本做估计,即以训练样本的样本均值x—(i)和样本方差 Si作为μi和∑i的估计,此时,

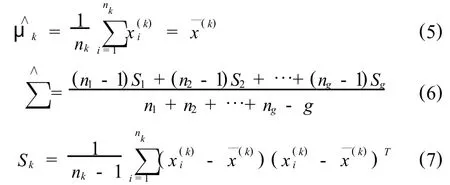
式中,k=1,2,…,g.

1.4 多正态总体的Bayes判别准则

设总体 G1,G2,…,Gg的先验概率分布分别为, q1,q2,…,qg,误判损失为,c(j|i)(i,j=1,2,…, g,i≠j),记c(i|j)=0.在等误判损失下,其Bayes判别准则为,

多正态总体Bayes判别准则可解释为:对于给定的样品x,计算g个总体在x处的概率密度函数值(以Bayes函数值 Wi(x)代替),最大值所属的总体Gi即为x所属的类别.

1.5 判别准则的评价

为考察上述判别准则的优良性,采用以训练样本为基础的刀切法来计算误判率 pw.该方法的基本思想是:每次从训练样本中剔除一个样本,利用剩下的 n1+…+ng-1个训练样本建立判别函数,再用所得到的判别函数对剔除的样本进行分类,重复以上步骤,以其误判的比例作为误判概率的估计.具体过程如下:

①从总体G1,容量为n1的训练样本开始,依次剔除其中的一个样本,用剩下的(n1-1)+…+ng个样本,建立相应的判别函数;

②利用得到的判别函数对剔除的样本做判别;

③重复步骤 ①、②直到总体G1中n1个样本依次被剔除和判别,其中被误判的样本数记为 n′1;

④利用上面的方法,继续对 G2,…,Gg中的样本进行剔除和判别,直到所有n1+…+ng个样本均被剔除和判别后,得到误判的训练样本总个数为n′1+…+n′g,其误判率为,

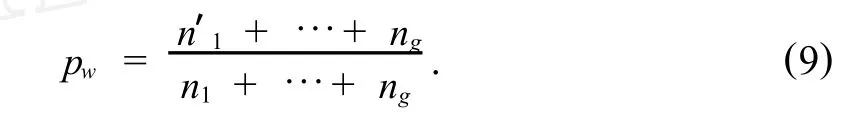
2 沉积环境评判的Bayes模型

2.1 评判因子

沉积物粒度参数的变化受搬运介质、搬运方式、沉积环境和气候等因素控制,参考相关研究成果[2-6],本文选择粒度的平均粒径、标准偏差、偏差、峰值等4个指标作为判别因子,并将沉积环境分为潮汐水道、水下分流河道和水下决口扇3种沉积环境,建立沉积环境综合评判的Bayes模型.

2.2 Bayes判别函数及判别实例

珠江口盆地某凹陷是晚新生代古珠江三角洲—滨岸沉积体系形成、发育及演化的主要场所.我们在对该凹陷某区域进行沉积微相划分时进行了大量的粒度实验,得到了一系列与沉积微相对应的粒度数据,取其中20个样本作为训练样本,建立Bayes判别函数,其具体样本数据如表1所示.

假定:误判损失相等,总体先验分布相同,并且3个总体服从协方差矩阵相等的正态分布,并按上述方法建立Bayes判别函数.

首先,计算相应的判别函数,具体过程如下:

由表1中的样品可知,

根据式(5)计算得到:

(1)计算各判别变量的均值.

表1 3种沉积环境的样本数据

(2)计算各判别样本的方差.

根据式(6)、(7)得到:

根据式(4)计算得到判别函数:

(3)判别准则的评价.

从总体潮汐水道,容量为 n1=5的训练样本开始,依次剔除其中的一个样本,用剩下的(n1-1)+…+ng=19个样本,建立相应的判别函数,并对剔除的样本做判别,重复上述操作,直到潮汐水道中n1=5个样本依次被剔除和判别,得到被误判的样本数记为,n′1=1;利用上面的方法,继续对水下分流河道、水下决口扇中的样本进行剔除和判别;直到所有 n1+…+ng=20个样本均被剔除和判别后,得到误判的训练样本总个数为,n′1+…+n′g=1+ 2+1=4,误判率为,

为了检验上述判别方法的有效性,我们利用所得到的判别函数对其余的55个粒度参数进行判别分析,其判定结果见表2.

表2 55个样本的识别结果

由表2可知,样本整体准确率为80%.由此可见,本文所提出的Bayes判别模型具有较高的工程适用价值.

3 结 语

沉积环境判别与分类是一个较为复杂的问题,还有许多的问题需要研究和解决.本文结合多元统计数学知识,以Bayes判别分析方法建立沉积环境综合评判的数学模型,为沉积环境的判别与分类提供了一种数量化与定量化的途径.同时,由于模型采用刀切法对判别准则进行评价,结果较为客观合理,因而具有较高的工程实用价值.

[1]赵澄林,朱筱敏.沉积岩石学(第三版)[M].北京:石油工业出版社,2001.

[2]曲政.沉积物粒度数据表征方法的研究[J].中国粉体技术,2001,7(4):24-31.

[3]薛太清.低渗透砂岩油藏沉积物粒度分布特征研究[J].沉积学报,2006,24(3):414-418.

[4]杨锐,雷怀彦.沉积物粒度参数的无偏估计及其在长乐海岸的应用[J].海洋地质动态,2007,23(10):33-36.

[5]张平,宋春晖.稳定湖相沉积物和风成黄土粒度判别函数的建立及其意义[J].沉积学报,2008,26(3):501-507.