Winkler地基上变厚度矩形板弯曲的微分求积解
杨 柳,彭建设,谢 刚,罗光兵
(1.西华师范大学物理与电子信息学院,四川南充 637002;2.成都大学工业制造学院,四川成都 610106; 3.西南交通大学牵引动力国家重点实验室,四川成都 610031)
0 引 言
在自然科学的研究中,各学科领域对于实际问题的研究,最终都将涉及到对偏微分方程的求解,目前,数值解已成为求解这些偏微分方程的主要方法.例如,有限元法、有限差分法、无网格法、微分求积法等[1-7].上述方法各有优缺点,并在不同的领域有成功的应用.Winkler地基上板的弯曲问题是一种常见的工程问题,本文运用微分求积法研究了Winkler地基上变厚度矩形板的弯曲问题.
1 Winkler地基上变厚度板的控制方程
在Winkler地基上,如果薄板的厚度发生变化则其抗挠度刚度D将不是常数,对该类型矩形薄板在载荷作用下其线性弯曲问题的控制方程为,

设 a,b分别为x,y方向的长和宽,将位置坐标做如下无量纲化转换,

于是,无量纲化后的控制方程可写为,

2 微分求积法原理
微分求积法以全域内节点函数值的加权和来逼近函数偏导数在某点的值,并在全域内运用高阶Lagrange多项式逼近域内某一待求函数.
设 g(x)为一待求函数,先沿 x轴设置N个节点,并以节点函数值,g(xi)(i=1,…,N),作为基本未知量,在全域内采用高阶Lagrange多项式插值逼近 g(x),
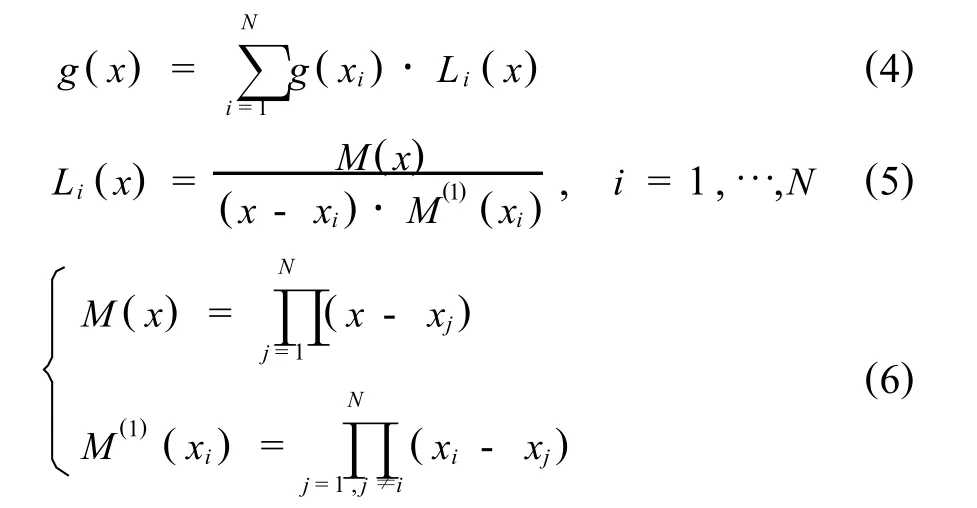
令g(x)的n阶导数在节点处的值为节点函数值的加权和,
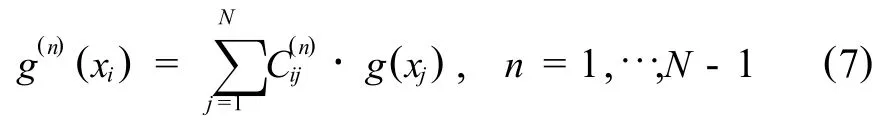
将式(4)~ (6)代入式(7),即可确定加权系数
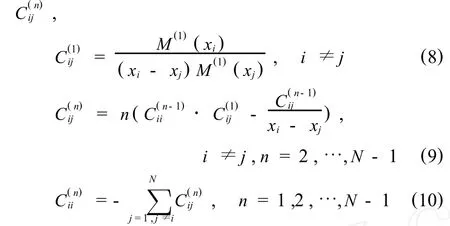
最后,由控制微分方程解出待定参数 g(xi),即求得 g(x)的数值解.
3 Winkler地基上变厚度板静力弯曲
在薄板上沿x方向取Nx个节点,沿y方向取Ny个节点.根据微分求积法原理,挠度 w对坐标的高阶偏导数在无量纲坐标为(ζi,ηj)的节点处的函数值可以用各节点的挠度值w(ζi,ηj)的加权和表示,对式(3)有微分求积方程,


其中,i=1,2,…,Nx;j=1,2,…,Ny.
由式(11)可见,全域内有 Nx×Ny个待定参数w(ζi,ηj),将其表达式表达为矩阵形式为,

其中,δ为Nx×Ny行的待定参数列阵,C表示为Nx× Ny行Nx×Ny列的权系数矩阵,F为Nx×Ny行的广义载荷列阵,C,F分别由式(12)的左边和右边形成.
考虑边界条件,矩形薄板有4个边界,共有8个边界条件.例如,四边简支时,其8个边界条件为,

即,
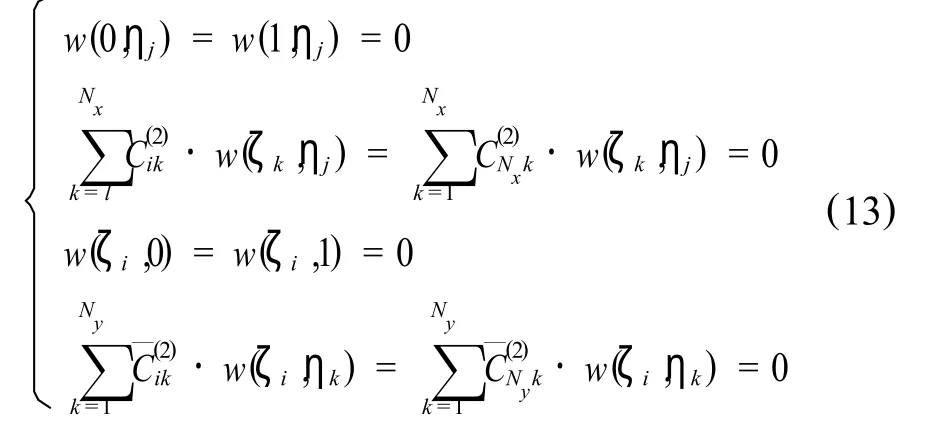
其中,i=1,2,…,Nx,j=1,2,…,Ny.
由此,可得4(Nx+Ny)个代表边界条件的微分求积约束方程.将式(13)分别取代式(11)中的 i= 1,2,Nx-1,Nx和j=1,2,Ny-1,Ny时表示的节点方程,取代后的方程即成为融入边界条件的可解线性方程组,从而得到式(12)中的待定参数列阵.如果在全域内求解该线性方程组即得节点位移w(ζi, ηj)的列阵δ,全域的位移场可由Lagrange插值得到,
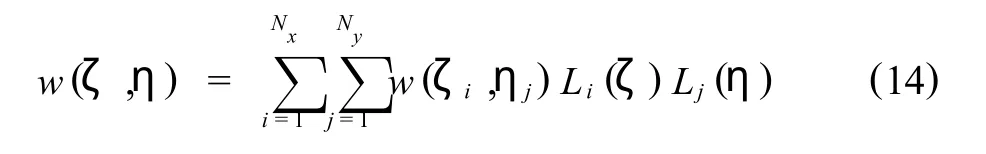
4 算 例
例1 Winkler地基上,一个四边简支的正方形板,在均布载荷 q作用下,求其中点处的挠度.
例2 Winkler地基上,一个四边固支的正方形板,在均布载荷 q作用下,求其中点处的挠度.
例3 Winkler地基上,一个四边简支的正方形板,受分布载荷q=q0y/a作用,板厚为 h(x,y)= [1+λ(2y/a-1)]h0,h0为y=a/2处厚度,取λ= 0.2,μ=0.25,求其 y方向中线的挠度.
例1~例3的解如表1~表3所示.
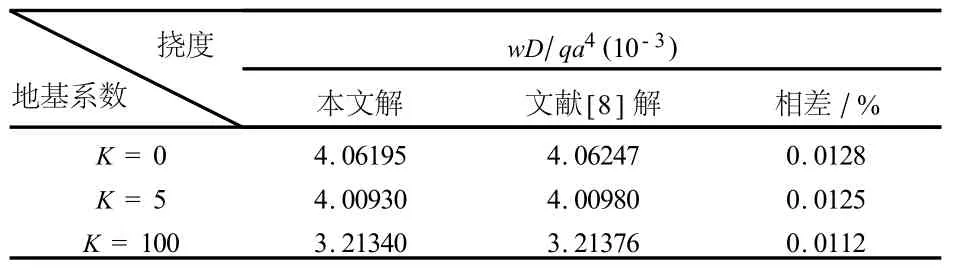
表1 Winkler地基上四边简支方板在均布载荷作用下中点挠度

表2 Winkler地基上四边固支方板在均布载荷作用下中点挠度
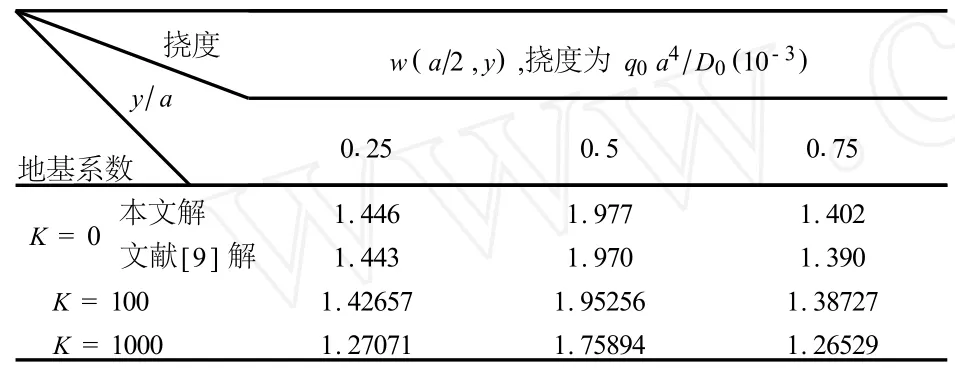
表3 Winkler地基上变厚度简支方板的挠度
5 结 语
本文采用微分求积法求解Winkler地基上变厚度矩形板的弯曲问题,给出了可参考的数据.从算例的计算结果可以看出,采用微分求积法对求解Winkler地基上矩形板弯曲,以及变厚度矩形板弯曲具有较高的精度.与多变量样条元法[8]和网格差分法[9]相比,微分求积法原理简单,适应性广,计算量小,程序易于在计算机上实现,是解决该问题的一种较好的数值方法.
[1]石东洋,关宏波.双曲型方程的非协调变网格有限元方法[J].纯粹数学与应用数学,2009,25(1):26-33.
[2]魏高峰,冯伟,高洪芬.基于位移插值的Voronoi单元有限元方法[J].应用力学学报,2008,25(2):342-346.
[3]Shu C,Wu W X,Ding H,et al.Free Vibration Analysis of Plates Using Least-square-based Finite Difference Method[J].Computer Methods in Applied Mechanics&Engineering,2007,196(7): 1330-1343.
[4]Li Z C,Chien C S,Huang,H T.Effective Condition Number for Finite Difference Method[J].Journal of Computational&Applied Mathematics,2007,198(1):208-235.
[5]彭建设,张鹰,杨杰.策动力下动力学初—边值问题的时域配点DQ空—时半解析法[J].计算物理,2000,17(1):45-48.
[6]刘燕,彭建设.Pasternak地基上自由边矩形板弯曲的DQ解[J].重庆工学院学报(自然科学),2009,23(2):44-49.
[7]张彬,孙立萍.变厚度矩形薄板弯曲问题的DQ法研究[J].唐山师范学院学报,2009,31(5):42-44.
[8]沈鹏程,何沛祥.多变量样条元法分析弹性地基板的弯曲、振动与稳定问题[J].应用数学和力学,1997,18(8): 725-733.
[9]李光耀,周汉斌.变厚度薄板弯曲问题的任意网格差分解法[J].应用数学和力学,1993,14(3):281-286.

