三维快速高精度地震波正演数值模拟方法及其应用

陈可洋

(中国石油大庆油田有限责任公司勘探开发研究院)

三维快速高精度地震波正演数值模拟方法及其应用

陈可洋

(中国石油大庆油田有限责任公司勘探开发研究院)

如何有效提高三维地震波正演数值模拟精度和计算效率一直是勘探地球物理学研究的重要问题。为了克服常规中心有限差分法较难快速提高差分精度的缺陷和一阶双曲型波动方程内存占用多、计算量大、引入变量较多的困难，采用高阶交错网格有限差分法直接求解三维地震波动方程，推导的高阶差分格式计算形式简单，可以推广于求解任意偶数阶时空导数，同时给出其稳定性条件。在人工边界处，对比了镶边法和常规旁轴近似法两种吸收边界条件。从三维似French模型的正演结果看出，采用的高阶交错网格差分算法在快速有效地提高数值模拟精度的同时，大大提高了计算效率，同时结合镶边法吸收边界条件还可有效压制边界反射，提高整个计算域内波场的信噪比。图3参5

三维地震波动方程 高阶交错网格有限差分法 正演数值模拟 镶边法吸收边界

0 引言

针对当前高精度地震勘探的要求，地震勘探方法必须考虑地下三维空间内非均匀介质对地震资料采集的影响。三维地震波正演数值模拟方法因此成为准确认识地震波场传播规律(保留几何学、运动学、动力学特征)、指导地震观测系统的优化设计和检验地震资料处理与解释方法准确性的一种重要手段。只有准确地研究复杂的地质构造和油气储集体所对应的地震波场特征，才能有效地进行构造和储层的识别与划分。传统的基于褶积模型的正演方法仅考虑了纵向上介质的变化，无法完整地描述三维空间的局部构造或非均匀性介质变化产生的复杂波场响应［1，2］。

目前，国内外对三维地震波的数值模拟方法进行了大量研究，逐步将二维方法推广应用于三维情况，主要包括单程波正演方法(如隐式有限差分法、Fourier法、傅里叶有限差分法、显式短算子方法等)和双程波正演方法(显式有限差分法、隐式有限差分法、有限元法、精细积分法、伪谱法、Hartley变换法等)，其中单程波正演方法是在频率－空间域进行交互处理，在每一步波场递推过程中，均需引入正反傅立叶变换，因而计算量较大。而双程波正演方法是在时空域进行计算的，因此其计算量较小，其中使用最多的是有限差分法，常规中心有限差分法较难快速提高有限差分精度，如果将标量地震波动方程转化为一阶双曲型方程来计算，则需要引入几个辅助变量，这将增加计算量和计算的复杂度。另外，对于大工区的三维地震波正演而言，其计算机内存的占用量是很庞大的，计算效率也必然较低。为了克服上述这些难题，本文在总结前人研究成果的基础之上，提出了将高阶交错网格有限差分法直接引入到求解三维标量地震波动方程的新思路，并结合镶边法吸收边界条件，以期快速提高局部地震波场的数值模拟精度和计算效率。

1 基本原理

1.1 三维高阶交错网格有限差分算子的构造

一般情况下，三维地震波动方程的形式如下:

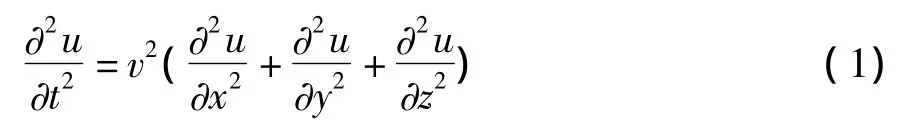
式中:

u—质点的振动位移;

v—介质速度;

t、x、y、z—分代表时间和三个空间方向。

以x方向为例，定义三维二阶导数的任意高阶交错网格有限差分格式如下:

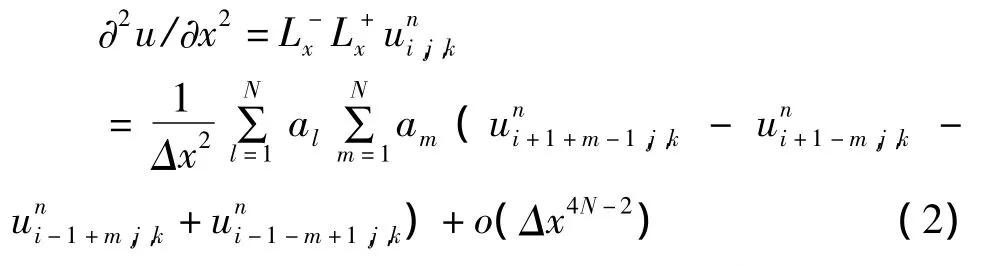
式(2)中，Lx=∂/∂x为x方向的空间微分算子，代表后向差分算子代表前向差分算子，二阶导数的差分算子就是将前向差分算子和后向差分算子组合得到，另外，(i，j，k，n)中的每一个量依次代表(x，y，z，t)的每一个方向的离散位置变量，am为高阶交错网格有限差分系数，N为差分阶数(正整数)。

将式(1)按照式(2)进行差分离散，得到的三维地震波动方程的时间2阶、空间4N－2阶交错网格有限差分法计算公式如下:

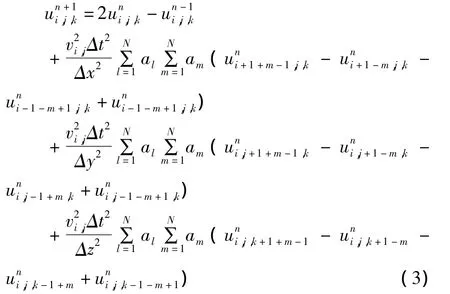
分析公式(3)可知，本文方法适用于非均匀网格的三维地震波正演数值模拟。此外可以看出，任意空间方向二阶导数的高阶交错网格有限差分格式具有差分规律，在相同差分阶数N情况下，常规中心网格有限差分法的差分精度为2N，而本文方法的差分精度为4N－2。由此可以看出，本文方法的差分精度与差分阶数N是近似4倍的关系，且为常规方法差分精度的2倍。另外，求解三维地震波动方程只需要引入三个不同时间层、相同的递推变量(即同一变量在三个不同时间层的不同表示)，而采用相同情况下的一阶双曲型方程则至少需要引入四个交错时间层、不相同的递推变量。因此，本文方法可以大大提高三维地震波正演数值模拟的计算效率。另外，文中的高阶差分方法还可以推广应用于求解任意偶数阶导数，仍以x方向为例，其计算通式为:其中2m为x方向导数的阶数。式(4)在高阶时间差分近似情况下较为常用(此时通常是将时间的高阶导数转化为空间高阶导数来实现)。

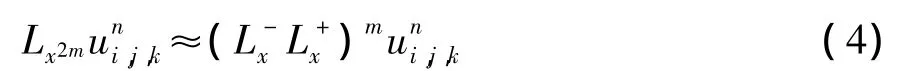
1.2 稳定性条件和吸收边界条件

经推导，式(3)的稳定性条件［3］与相应的一阶双曲型情况相一致，其表达式如下:

其中，S=Max{v2/Δx2，v2/Δy2，v2/Δz2}，在高阶时间差分近似条件下，Δt的上限值可以适当放宽。

为了能够削弱或消除计算边界处的反射波，同时保证边界计算过程的稳定，在人工截断边界处，采用了常规旁轴近似吸收边界条件［4］(不需要进行外侧镶边，仅依赖于边界附近节点处不同时间层的值，并采用二阶近似的单程地震波动方程来进行边界点值的预测，其计算效率最高，但受到边界吸收角度的限制)和一定厚度的外侧镶边法吸收边界条件［5］(即在3D模型的边界外侧，镶上20个网格节点的阻尼条带，使得边界反射波在该条带内多次吸收衰减，其精度较高，但效率偏低)两种方法，并对比这两种吸收边界条件对三维空间有效波场响应的影响。

2 应用实例

采用的速度模型类似于French模型，其中包含一水平层界面、一个倾斜断层、一个隆起构造、一个凹陷构造(图1，数值越大代表层界面离地表越深)，模型总大小为500m×500m×500m，三个方向空间网格大小均为5m，震源位于模型地表中央位置，其主频为60Hz，模型中上层介质速度为2000m/s，下层介质速度为2500m/s，时间步长为0.5ms，满足稳定性条件式(5)，时空差分精度为(Δt2+Δx10)(此时N=3)。检波器布置于地表下方50m深度处，自激自收方式合成的水平叠加剖面(这里考虑了速度差异界面反射系数的大小)，在三维模型的边界处分别采用常规旁轴近似吸收边界条件和一定厚度的外侧镶边法吸收边界条件。

图2分别为0.175s时刻，x、y、z三方向的中间位置且平行于yoz、xoz、xoy三个平面的波场快照切片，图中的①和②与图1中波场快照切片位置(虚线)相对应，边界处采用了外侧镶边法吸收边界条件。对比速度模型和波场快照可以比较容易地识别出直达波、倾斜界面的反射波、水平界面的反射波以及隆起构造的反射波这四种波，可以看出，地震波是在三维空间中进行传播的，仅考虑二维空间的传播问题是不准确的。另外，在地震波到达模型边界时无边界反射波形成，在波场传播过程中无任何频散现象，这表明本文算法精度较高。

图3(a)和图3(b)分别为采用镶边法吸收边界条件情况下的纵观测系统和非纵观测系统接收到的单炮模拟记录。分析图3(a)和图3(b)可知，边界反射波的能量较弱，而有效波能量强，同相轴清晰，结合速度模型可以较准确地识别出各种有效波的来源，从而可以进行三维空间地震波场的传播规律研究。图3(c)、图3(d)、图3(e)、图3(f)分别为采用常规旁轴近似吸收边界条件和镶边法吸收边界条件情况下接收到的两条正交的自激自收剖面(类似于水平叠加剖面，剖面位置如图1中的虚线位置所示，①代表x方向剖面位置，②代表y方向剖面位置)，比较x方向剖面(图3(c)和图3(d))和y方向剖面(图3(e)和图3(f))可知:采用旁轴近似吸收边界条件时，地震波场不清晰，比较杂乱，信噪比很低;而采用镶边法吸收边界条件后，有效波特征明显，同相轴易追踪。再结合三维速度模型和三维地震波的波场快照就可以很容易地识别出各种复杂地震波场的成因问题。

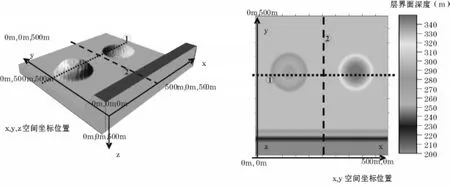
图1 三维似French速度型

图2 0.175s时刻，三维任意方向波场快照切片

图3 三维地震波数值模拟记录

3 结论

本文提出了用高阶交错网格有限差分法直接求取三维地震波动方程的新思路，并详细推导得到了三维地震波动方程的高精度离散方程，给出了计算所需的稳定性条件和吸收边界条件。从计算量、计算效率、计算复杂度上对比分析了本文方法和一阶双曲型方法，得出本文方法在三维快速高精度实现正演数值模拟方面的优点为:①计算速度快;②占用内存小;③计算格式简单有规律，且计算复杂度低;④计算量小。基于这些优点，本文方法可以用来快速模拟野外三维地震资料的采集过程以及观测系统的优化设计，同时还可以推广应用于三维二阶各向异性介质弹性波的传播数值模拟问题。

从分别采用外侧镶边法吸收边界条件和常规旁轴近似吸收边界条件的计算结果可以看出，前者边界吸收效果好，三维模拟记录中无任何频散现象，能够较清晰地识别出各种构造所形成的复杂反射波，而后者边界反射波与有效波相互叠加，造成了信噪比降低，有效波场模糊、难识别。因此，采用本文方法并结合镶边法吸收边界条件就可以快速有效地模拟三维地震波的传播规律。

1 陈可洋，刘洪林，杨微，等.随机介质模型的改进方法及应用［J］.大庆石油地质与开发.2008，27(5):124－126，131.

2 陈可洋.三维随机建模方法及其波场模拟分析［J］.勘探地球物理进展，2009，32(5):315－320.

3 陈可洋.标量声波波动方程高阶交错网格有限差分法［J］. 中国海上油气，2009，21(4):232 －236.

4 杨微，陈可洋.加权吸收边界条件的优化设计［J］.石油物探，2009，48(3):244 －246，251.

5 陈可洋.边界吸收中镶边法的评价［J］.中国科学院研究生院学报，2010，27(2):170 －175.

3D FAST AND HIGH－RESOLUTION SEISMIC－WAVE FORWARD NUMERICALSIMULATION AND ITS APPLICATION

CHEN Keyang(Research Institute of Exploration and Development，PetroChina Daqing Oilfield Company)．

How to effectively increase both accuracy and calculation efficiency of 3D seismic－wave forward numerical simulation is an important problem in geophysical prospect．But for conventional central finite－ difference method，it is difficult to fast improve difference accuracy;and for one－stage dual－curve wave equation，there are some defects of occupying much memory，large amount of calculation and introducing much variable．In this study，a method of higher－order staggered－grid finite difference is adopted to directly solve a 3D seismic wave equation and there are some advantages:(1)simple calculation form;(2)it may also be applied to solving a random even－order space－time derivative;(3)it can provide with some stable conditions．Moreover，edging method is correlated to conventional paraxial approximation to adsorb in boundary condition．It is shown from the forward result of 3D quasi－French model that:(1)the higher－order staggered－grid finite difference method can not only fast and effectively improve simulation accuracy but also increase calculation efficiency;and(2)combined with edging method，the higher－order staggered－grid finite difference method can effectively impose boundary reflection and improve signal－to－noise ratio of wave field within whole calculation domain．

3D seismic wave equation，higher－order staggered－grid finite difference method，forward numerical simulation，edging method

陈可洋，男，1983年出生，助理工程师;2009年获大庆石油学院地球探测与信息技术专业硕士学位，现主要从事高精度弹性波正演数值模拟及逆时偏移成像方法研究。地址:(163712)黑龙江省大庆市让胡路区大庆油田勘探开发研究院地震处理二室。电话:(0459)5508524，13504595794。E － mail:keyangchen@163.com

(修改回稿日期 2010－12－30 编辑 陈 玲)NATURALGAS EXPLORATION＆DEVELOPMENT．v．34，no．3 ，pp．12－15，7/25/2011