一类受持续扰动的非线性时滞系统的扰动抑制*

高洪伟,唐功友

(1.青岛农业大学机电工程学院,山东青岛266109;2.中国海洋大学信息科学与工程学院,山东青岛266100)

一类受持续扰动的非线性时滞系统的扰动抑制*

高洪伟1,唐功友2

(1.青岛农业大学机电工程学院,山东青岛266109;2.中国海洋大学信息科学与工程学院,山东青岛266100)

研究一类受已知动态特性的外部扰动作用的非线性时滞系统的扰动抑制问题。基于内模原理构造能够抵消扰动影响的伺服补偿器,然后利用极大值原理及灵敏度法设计带有补偿器的最优控制律,使得系统在无扰动作用时以1种最优方式运行,而有扰动作用时,控制律能够消除扰动引起的稳态误差,实现无静差扰动抑制。最后,通过仿真算例验证提出算法的有效性。

非线性时滞系统;内模原理;最优控制;扰动抑制;灵敏度法

在化工过程、交通、生物、热交换系统和网络控制等系统中,普遍存在着非线性时滞系统,而阶跃扰动、斜坡扰动及满足某一类齐次微分方程的信号等持续扰动,广泛存在于海洋平台的实时控制[1]、飞机飞行姿态控制[2]以及工业机械[3]等系统当中。时滞系统的稳定性分析与控制算法的综合是重要的研究课题,许多学者在理论和实践上进行了大量的研究工作[4-7]。近年来,扰动抑制备受关注,并取得了一定的成果。滑模控制对有界干扰和参数变化具备鲁棒性,可以削弱由于负载变化或随机干扰对系统控制性能的影响,但存在抖振问题[8];Bodson针对受正弦扰动的系统提出了自适应扰动抑制算法[9],Pi等构造了扰动观测器用于估计和补偿外界扰动[10];针对有界扰动,唐等利用前馈反馈控制技术实现了受扰控制系统的近似最优扰动抑制[11],但前馈技术不能实现无静差控制;内模原理[12]是抑制干扰的1种有效手段,将干扰视为由1个外部动态系统产生的信号,若控制回路内包含产生干扰的动态系统的全部信息,则可完全消除干扰的影响,实现无静差控制。对于受持续扰动的非线性时滞系统,由于系统本身和设计控制的复杂性,目前的研究成果相对较少,尚有许多问题亟待解决。

本文研究受持续扰动的非线性时滞系统的扰动抑制问题。首先利用内模原理,构造扰动补偿器并置于闭环控制系统的反馈通道以抵消扰动对系统的影响。然后基于灵敏度法,将具有二次型性能指标的最优控制问题所导致的非线性两点边值(TPBV)问题,化为线性TPBV问题,求解该线性TPBV问题得到最优控制律,继而求得原控制系统的无静差扰动抑制控制律。

1 问题描述

考虑受扰的时滞非线性系统

其中x∈Rn,u∈Rp,y∈Rm和w∈Rm分别是状态,控制,输出和扰动向量,f(x):Rn→Rn是关于x的各阶导数连续的非线性函数向量,且f(0)=0,A,A1,B,C和D是具有适当维数的常数矩阵,<(t)为已知的连续初始向量函数,τ>0为常数时滞项。扰动w由以下外系统产生

假设1 矩阵(A,B)是完全可控的。

假设2 dim(u)≥dim(y)。

假设3 对于矩阵G的每个特征值θj,都有

2 主要结果

2.1 补偿器设计

为消除扰动对系统的影响,利用内模原理构造如下伺服补偿器

其中z0为常数。将内模扰动补偿器与系统(1)串联得

记作

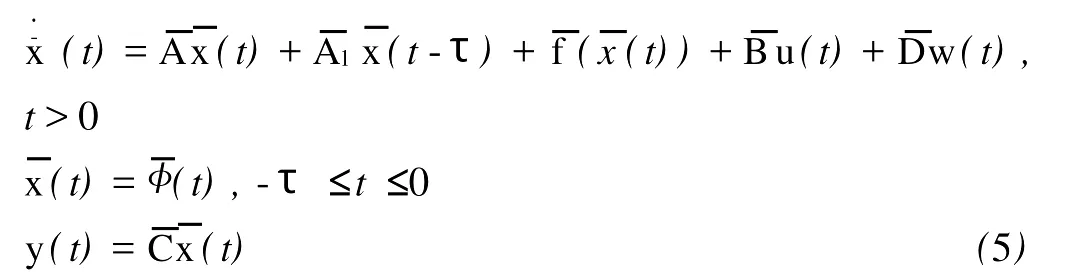
其中

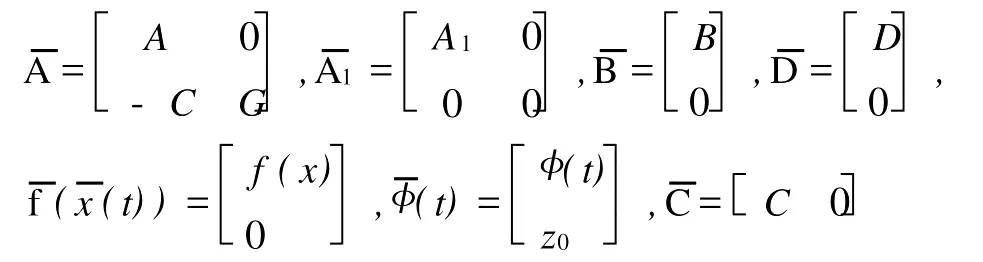
对于系统(5),要实现的是寻求一控制律使其闭环稳定且稳态输出误差为0。

2.2 控制器设计

考虑系统(5)的闭环稳定问题时可以不考虑扰动的影响,即可假定扰动w(t)=0。因此,对于无扰动作用的系统(5),可以考虑其最优控制问题,以极大值原理来设计使系统闭环稳定的最优控制律。选取如下二次型性能指标

其中Q=block-diag{Q0,Q1},Q0是半正定矩阵且满足最优调节器的一般条件,Q1和R是正定矩阵。

由假设1知,rank[s I-A和B]=n。当s≠θj(j=1,2,…m),即s不是G的特征根时,rank[s I-G]=m显然成立。因此有下式成立

当s=θj(j=1,2,…m),即s是G的特征根时,

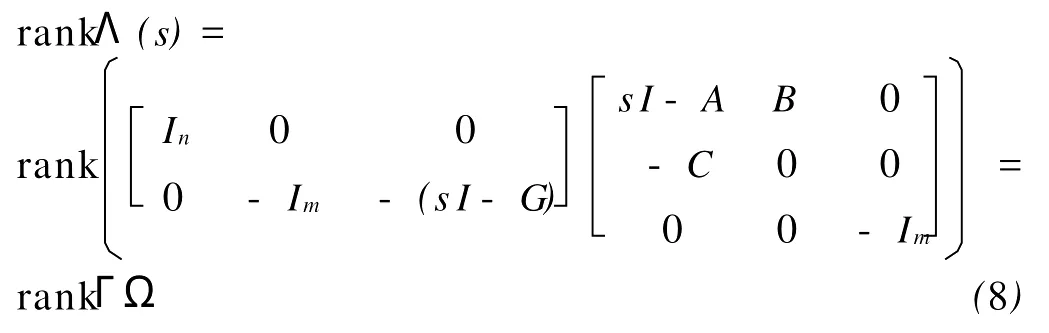
由假设3可得rankΩ=n+2m。而由(G,Im)完全可控知,rankΓ=n+m。因此,利用Sylvester不等式,可以证得(7)成立。综上分析,(?A,?B)是完全可控的。又Q0是半正定矩阵且满足最优调节器的一般条件,Q1和R是正定矩阵。因此系统(5)关于性能指标(6)的最优控制律存在且唯一。根据最优控制问题的必要条件可以导出

和最优控制律

考虑到TPBV问题(9)的解析解一般是不存在的,引入1个与时间t无关的实标量灵敏度参数ε(0≤ε≤1),构造变量函数和,则问题(9)被转化为如下新的TPBV问题

最优控制律具有如下形式

其中

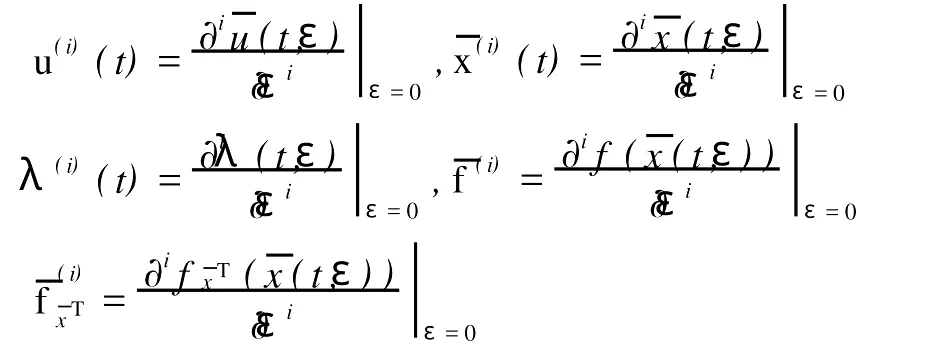
将(13)代入(12),并令ε=1可得最优控制律的表达式为

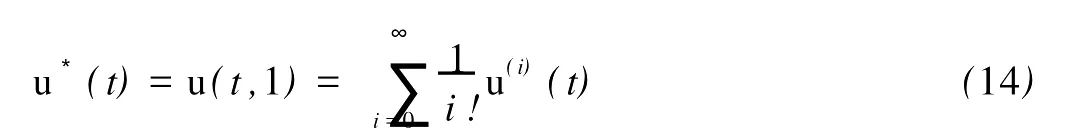
定理1 如果假设1～3的条件成立,且矩阵对(?A,Q1/2)完全可观测,那么系统(5)关于性能指标(6)的最优控制律为

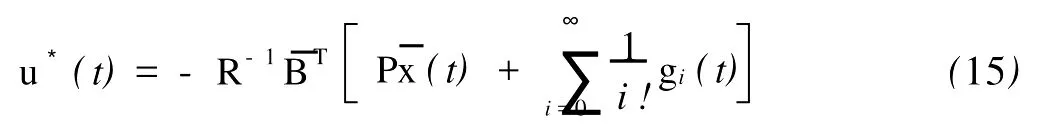
其中P是下列Riccati矩阵方程的唯一正定解

gi(t)由下列第i阶伴随向量微分方程求得

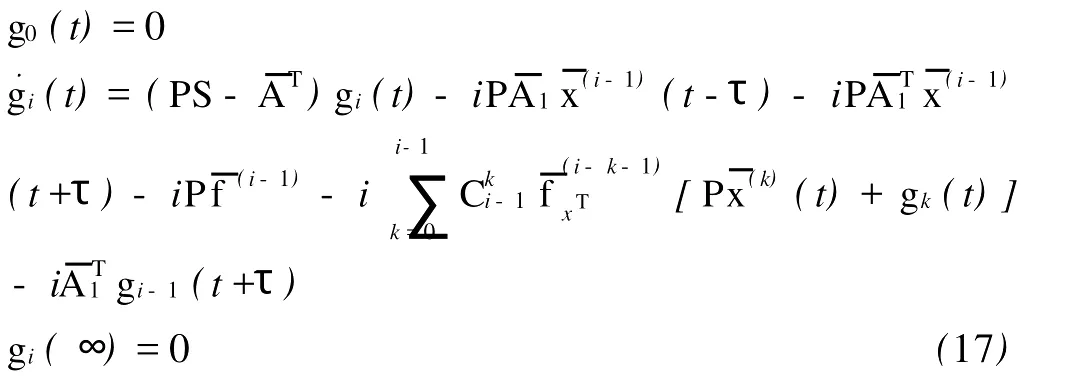
x(i)(t)由微分方程(18)和(19)求得

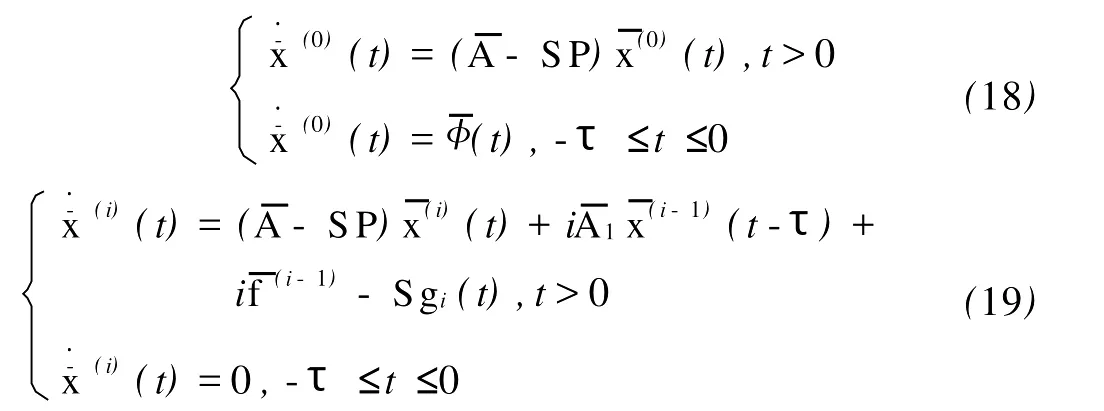
证明 将各函数的Maclaurin级数展开式(13)代入含灵敏参数ε的TPBV问题(11),并比较等式2边ε的同次项,可得

将(13)代入含灵敏度参数的最优控制律(12),比较等式2边ε的同次项,得

由(14)可知,只要得到u(i)(t),即可求得系统的最优控制律。令

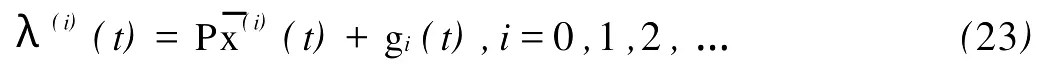
其中g0(t)=0。将(23)(i=0时)代入(20)第1,2式可得矩阵Riccati方程(16)。由矩阵对完全可控,且完全可观测,因此Riccati矩阵方程(16)有唯一的正定解矩阵P。由(23),(20)和(21)可得(18)和(19)。将(23)(i=1,2,…时)2边求导并将(19)代入,得到

将(24)与(21)的第2式等式2边相加,并利用(23)和(16),即可得到求解伴随向量的微分方程(17)。由线性系统最优控制理论知,矩阵的所有特征值都具有负实部,且伴随向量方程(17)中,和的算法见文献[13])都是已知项,因此求解gi的过程是一个线性迭代过程,而且对任意的t,gi(t)的终值有界,并有gi(∞)=0。

将(23)代入(22),得到

通过以上讨论可知,x(i)(t)和gi(t)可通过迭代求解一族线性状态向量方程(18),(19)和线性伴随向量方程(17)求得,矩阵P可通过求解Riccati矩阵方程(16)得到。因此,将(25)代入(14)即可得到系统(5)关于性能指标(6)的最优控制律(15)。证毕。

注1 最优控制律(15)由状态反馈项和1个级数项组成。如果系统(5)不存在时滞项和非线性项,即?f(?x)=0,则由(17)得,gi(t)≡0(i=1,2,…),这说明最优控制律中的级数项的作用是补偿时滞及非线性特性对系统的影响。

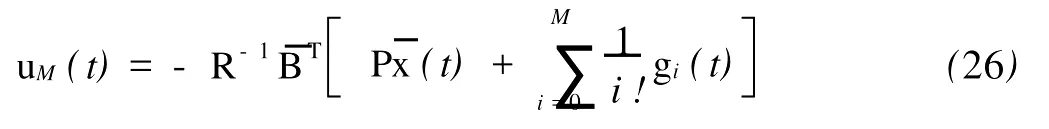
实际中次优控制迭代的次数可以按要求满足的控制精度来确定。给定控制精度δ>0,每迭代一次,计算性能指标Ji。当

令M=i(其中L是某个给定的正整数),因此可得到系统的次优控制律uM(t)。

令P=[P1P2],则控制律(26)可以写成

从图1可以看出,控制律(28)由精确的状态反馈项、内模补偿项以及伴随向量的级数和形式的补偿项组成,其中状态反馈项用以镇定控制系统,内模补偿项用以抵消扰动对系统的影响,伴随向量的级数和形式的补偿项则用以补偿非线性项对系统的影响,因此当系统存在扰动时,内模可以补偿扰动引起的稳态误差,控制律(28)即为系统(1)的无静差扰动控制律。

图1 控制系统结构图Fig.1 Structure of the control system s

3 仿真

考虑由系统(1)描述的非线性系统,其中

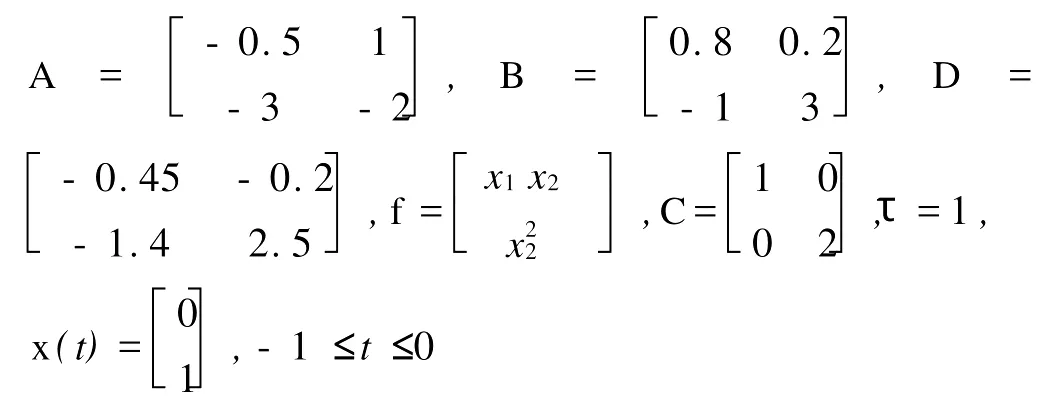
由外系统(2)描述的扰动,其中

设计扰动补偿器为

选取由(6)描述的性能指标,其中

(1)当w(t)=0时,受控系统在不同迭代次数下性能指标的值见表1。

表1 不同迭代次数的性能指标Table 1 Perfo rmance index values at different iteration times

从表1可以看出,J0>J1>…>J4,即随着迭代次数的增加性能指标的值不断减小且最终收敛于1个稳定的最优值J*。令δ=0.005,L=2,则|(J2-J4)/J4|=0.003 8<δ,这说明经5次迭代可以满足控制精度要求,因此第4阶控制律u4可以看作是系统(5)的近似最优控制律。当w(t)=0时,输出及控制律的曲线见图2～5。由图可以看出,当系统不受扰动作用时,本文设计的控制律能使系统以较快的速度收敛于最优轨线,所需的控制力也随迭代次数的增加而减小。

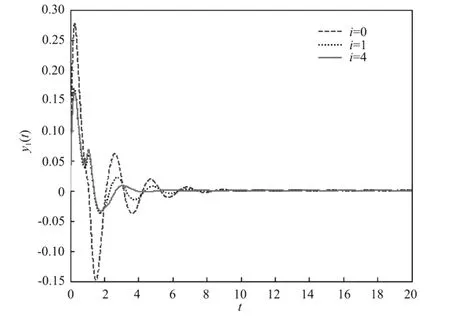
图2 输出y1的仿真曲线Fig.2 Simulation curves of the output y1

图3 输出y2的仿真曲线Fig.3 Simulation curves of the output y2

图4 控制u1的仿真曲线Fig.4 Simulation curves of the control law u1

(2)当系统受发散扰动作用时,系统的仿真曲线见图6,从图中可以看出,当t→∞时,系统的输出稳态误差为与零,所以本文设计的控制器能够实现无静差扰动抑制。

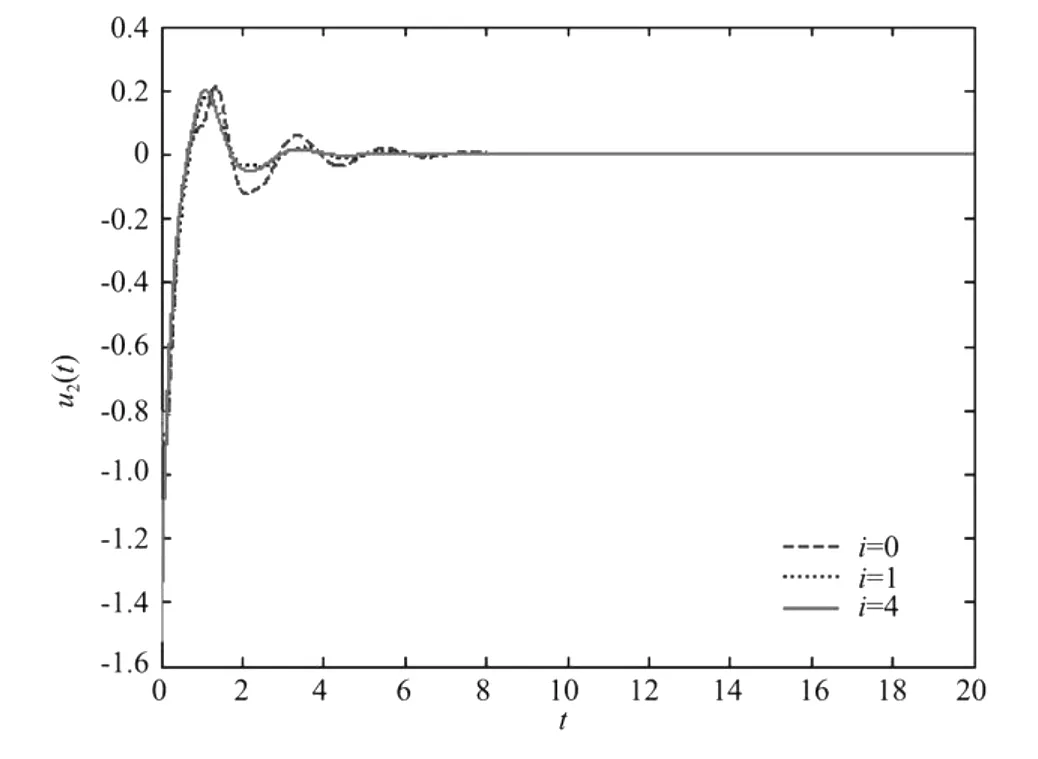
图5 控制u2的仿真曲线Fig.5 Simulation curves of the control law u2

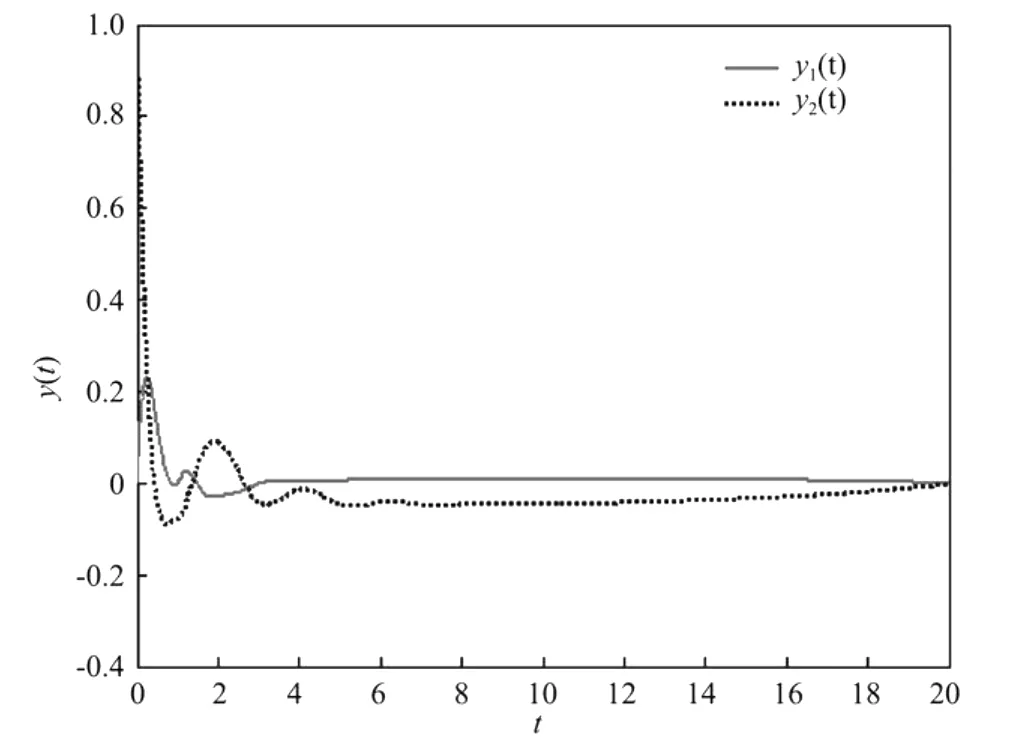
图6 有扰动作用时系统输出曲线Fig.6 Simulation curvesof the output

4 结语

针对一类受持续扰动的非线性时滞系统,基于内模原理构造了扰动伺服补偿器,并将其植入受控系统的反馈通道,与受控系统串联组成1个增广系统。然后,利用极大值原理和灵敏度法,设计了能够补偿状态时滞和非线性对系统影响的增广系统的最优控制器。当系统受非渐近稳定的扰动的影响时,由于得到的控制律中包含能够抵消扰动影响的内模状态,因此能够消除扰动引起的输出稳态误差,实现无静差扰动抑制。最后通过仿真研究验证了本文提出的方法的有效性。

[1] Ma H,Tang G Y,Zhao Y D.Feedforward and feedback optimal control for offshore structures subjected to irregular wave forces[J].Ocean Engineering,2006,33(8-9):1105-1117.

[2] Mulgund S S,Stengel R F.Optimal nonlinear estimation for aircraft flight control in wind shear[J].Automatica,1996,32(1):3-13.

[3] Hamer A J,Angelis G Z,Roozen N B.Broad-band active vibration suppression using PPF focused on industrial application[J].IEEE/ASM E Transactions on Mechatronics,2005,10(2):146-153.

[4] Li Juan,Tang Gong-You.Fault diagnosis for networked control systems with delayed measurements and inputs[J].IET Control Theory&Applications,2010,4(6):1047-1054.

[5] 李娟,唐功友.基于观测器的离散时滞系统的故障诊断[J].控制与决策,2010,25(8):1220-1224.

[6] Su C L,Wang SQ.Robust model predictive control for discrete uncertain nonlinear systems with time-delay via fuzzy model[J].Journal of Zhejiang University:Science A,2006,7(10):1723-1732.

[7] Mahmoud M S,Ismail A.New resultson delay-dependent control of time-delay systems[J].IEEE Transactions on Automatic Control,2005,50(1):95-100.

[8] Guo Y S,Chen L.Terminal sliding mode control for coordinated motion of a space rigid manipulator with external disturbance[J].App lied Mathematics and Mechanics,2008,29(5):583-590.

[9] Bodson M.Performance of an adaptive algorithm for sinusoidal disturbance rejection in high noise[J].Automatica,2001,37:1133-1140.

[10] Pi Y J,Wang X Y.Observer-based cascade control of a 6-DOF parallel hydraulic manipulato r in joint space coo rdinate[J].M echatronics,2010(20):648-655.

[11] 唐功友,高德欣.带有持续扰动非线性系统的前馈-反馈最优控制[J].控制与决策,2005,20(4):366-371.

[12] Francis B A,Wonham W M.The internalmodel p rincip le of control theo ry[J].Automatica,1976(12):457-465.

[13] Tang G Y,Fan M Q.Series-based app roximate app roach of optimal tracking control for nonlinear system swith time-delay[J].Progress in Natural Science,2008,18(12):1571-1576.

Disturbance Rejection fo r a Class of Nonlinear Time-Delay System swith Persistent Disturbances

GAO Hong-Wei1,TANG Gong-You2
(1.College of Mechanical and Electronic Engineering,Qingdao Agricultural University,Qingdao 266109,China;2.College of Info rmation Science and Engineering,Ocean University of China,Qingdao 266100,China)

This paper is concerned with the disturbance rejection p roblem for nonlinear system s with time-delay affected by additive persistent disturbanceswith know n dynamic characteristics.In order to achieve a zero steady-state erro r disturbance rejection,a disturbance compensato r is constructed based on the internalmodel p rinciple.Then,an op timal control law with a compensation term is designed by the maximum p rincip le and the sensitivity app roach,w hich can realize the op timal control w hen the system has none disturbances.W hile the disturbance exists,this obtained contro l law can reject the disturbance with zero steady-state erro r because of the existence of the internalmodel.Simulation examp les show the effectiveness of the presented algorithm.

nonlinear time-delay system s;internal model p rincip le;optimal control;disturbance rejection;sensitivity app roach AMS Subject Classifications: TP13

TP13

A

1672-5174(2011)09-103-06

国家自然科学基金项目(60574023,40776051);山东省自然科学基金重点项目(Z2005G01);青岛农业大学高层次人才启动基金项目(630805)资助

2011-01-23;

2011-06-20

高洪伟(1979-),女,博士。E-mail:gaohw97@126.com

责任编辑 陈呈超