基于数学形态学算法的纸病检测及IDL应用

陈 宁

（天津科技大学电子信息与自动化学院，天津，300222）

基于数学形态学算法的纸病检测及IDL应用

陈 宁

（天津科技大学电子信息与自动化学院，天津，300222）

本文介绍了采用数学形态学算法从纸样图像中提取纸病的方法。运用第四代计算机语言IDL(Interactive Data Language)完成了数学形态学的膨胀、腐蚀及梯度运算，并实现了纸样图像中纸病边缘的检测，结合阈值分割方法得到纸病检测和分割结果

数学形态学 纸病检测 IDL数字图像处理

1 引言

制浆造纸过程是高度复杂的生产过程。在各工艺过程中，由于设备磨损、生产原料变化、操作不当或环境污染等原因，会造成多种外观纸病，例如：斑点、孔洞、尘埃、褶皱、条痕和纸边裂口等[1]。这些不仅直接影响成品的使用，而且影响纸的其他物理性能指标，甚至还决定成品的损耗情况。目前，运用数字图像处理技术，分析研究纸张灰度图像的基本特征和分布状况，达到判断纸病类型、提取纸病区域的目的，是智能化纸病检测的主要方法之一。

数学形态学是基于集合论的研究数字图像形态结构特征与快捷并行处理方法的理论，它从集合的角度分析图像，通过对目标图像的形态变换实现结构分析和特征提取的目标，属于一种非线性图像处理和分析理论，近年来被广泛应用于图像分析中[2]。

IDL(Interactive Data Language)是美国RSI公司开发的第四代计算机语言。它将多种数学分析与图形显示技术结合在一起，具有开放性、高维处理能力、科学计算能力及可视化分析的特点[3]。目前它已经成为二维及多维数据可视化分析与应用开发的理想工具之一。本文探讨利用IDL实现数学形态学运算，从纸样图像中检测纸病的方法。

2 检测原理

2.1 灰度数学形态学基本运算

图像分析中的数学形态学是以形态为基础对图像进行分析的数学工具。它的基本思想是用具有一定形态的结构元素，去量度和提取图像中的对应形状，以获取对图像分析和识别的效果[4]。

数学形态学的数学基础是集合论，其算法具有并行实现的特征，它的处理对象可以是二值图像也可以是灰度图像。数学形态学中两个最基本的形态操作是互为对偶运算的膨胀和腐蚀，将二者结合可产生不同的形态学变换，典型的有开运算和闭运算。

设：一幅灰度值图像 F=f(x,y)，(x,y)∈R2，其中(x,y)为图像上点的坐标，f(x,y)为(x,y)处的灰度值。b(i,j)代表结构元素，它本身也是一幅子图像。

2.1.1 膨胀运算与腐蚀运算

用结构元素b(i,j)对输入图像f(x,y)进行灰度膨胀记为f b，其定义为

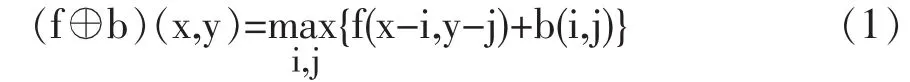
用结构元素b(i,j)对输入图像f(x,y)进行灰度腐蚀记为，其定义为

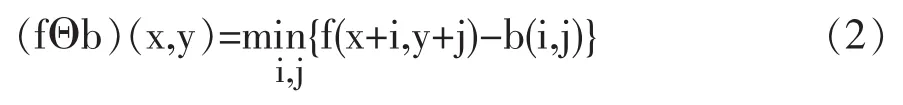
膨胀运算是一种扩张变换，它以结构元素b(i,j)为模板，以某像素点为中心平移通过图像，搜寻图像在结构元素大小范围内的灰度和的极大值；腐蚀运算则是一种收缩变换，与膨胀互为对偶运算。

2.1.2开启运算与闭合运算

用结构元素b开启图像f记为fob；用结构元素b闭合图像f记为fgb，其定义分别为：

开启操作，即先腐蚀后膨胀的过程，它具有消除与结构元素相比，尺寸较小的亮细节，而保持图像整体灰度值和大的亮区域基本不受影响的作用。

闭合操作，即先膨胀后腐蚀的过程，它具有消除与结构元素相比尺寸较小的暗细节，而保持图像整体灰度值和大的暗区域基本不受影响的作用。

2.2 基于形态学的纸病图像检测与分割

在造纸过程中纤维长短和分布的随机性，导致纸张的灰度数值是随机的，纸病特征隐含其中。研究发现对于有孔洞的纸张，其孔洞的灰度数值和正常纸样灰度差异较大，可采用阈值法判定孔洞纸病。但是对于有些纸病，如褶子、皱纹、斑点、硬质块、条痕、毛毯印等纸病，其灰度数值和正常纸样的灰度数值差异不大，简单地采用灰度阈值的方法很难得到理想的检测效果，运用数学形态学算法对含有纸病的数字图像进行灰度变换，增强纸病区域与正常纸样的灰度差，进而有效地检测纸病区域。本文将采用边缘提取的办法完成纸病图像的检测和分割。

边缘表示图像灰度发生空间突变或者在梯度方向上发生突变的像素集合。图像边缘和图像内容的物理特性之间存在着直接的联系，包含了图像的大部分信息。很多传统的图像边缘检测算子，如Roberts算子、Sobel算子和Prewitt算子等均是通过计算局部微分完成工作，这些算子普遍存在的不足是对噪声敏感，当图像较复杂或含有噪声时，其边缘检测的效果不够理想。近年来提出的LOG和Canny边缘检测算子，利用高斯函数对原始图像作平滑或卷积运算以抑制噪声，显现出计算量较大、边缘定位精度较差之缺陷。而数学形态学以对称的结构元素作用于数字图像，且结构元素的形态又决定了运算所提出的形态信息，所以用形态学梯度算子完成边缘检测，所得到的结果在边缘的连续性及各向同性方面都优于传统方法，对图像细节和边缘定位也得到了较理想的效果。

采用膨胀运算时，边缘检测形态梯度算子为

采用腐蚀运算时，边缘检测形态梯度算子为

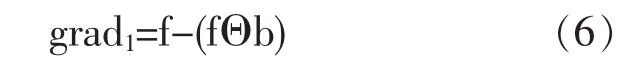
膨胀与腐蚀结合使用时，边缘检测形态梯度算子为

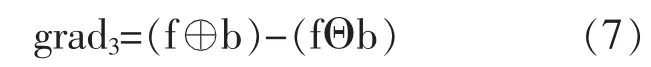
结构元素尺寸的选取对去除噪声和保护图像细节非常重要，小尺寸结构元素去噪能力弱，但能很好地检测边缘细节；大尺寸结构元素去噪能力强，但检测到的边缘较粗。

2.3 纸病检测的形态学IDL算法

根据纸病图像的特点，应用IDL语言完成纸病检测的形态学算法，其基本过程与程序为：

（1）读入纸样图像，将其存入变量img；

（2）构建半径为2的圆形结构元素strucElem；

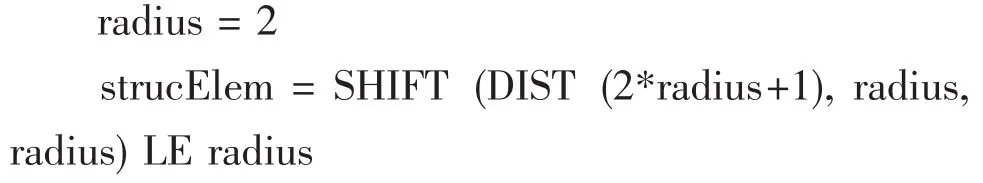
（3）对原图像边缘进行处理，以免数学形态运算造成图像边缘数据的不确定性；

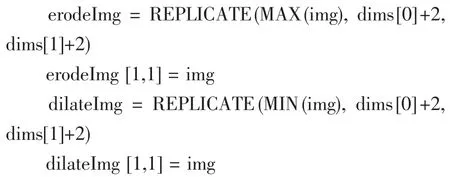
（4）调用膨胀函数 DILATE（），完成灰度膨胀处理；

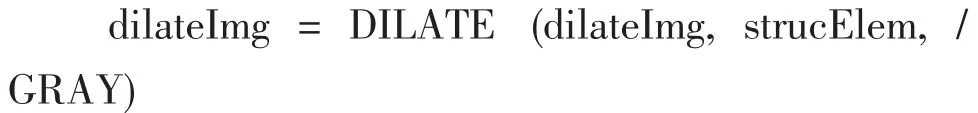
（5）调用腐蚀函数 DILATE（），完成灰度腐蚀处理；

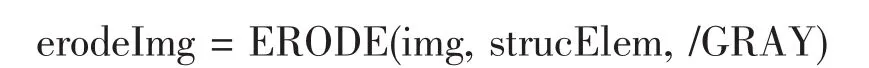
（6）用形态学梯度算子完成边缘检测及阈值分割；

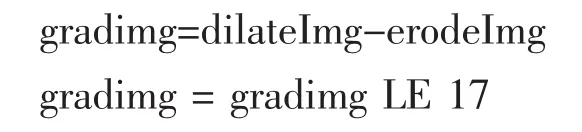
3 实验结果

如图1所示是一幅含有孔洞、斑点及皱褶的纸病图像。为保证得到较细的边缘和较理想的各向同性，本文选用半径为2的圆形结构元素，梯度算子选用膨胀与腐蚀相结合的方式。

图2与图3分别为对原图进行膨胀与腐蚀的处理结果，可以看出，本文选用的结构元素其膨胀操作的结果减弱了原图中的暗细节，而腐蚀操作的结果则减弱了原图中的亮细节。图4与图5分别为梯度算子的操作结果及后续采用阈值法进行图像分割的结果。可以看出，它基本提取出了原图中的孔洞、斑点、皱褶的纸病特征。

4 结束语

由于造纸工业复杂的生产过程及原料的变化，使纸张表面光学性能具有随机性，其图像表现为含有大量的随机噪声。数学形态学作为一种非线性滤波方法，其基本运算的应用，能十分有效地滤除图像中的随机噪声。基于图像灰度的数学形态学腐蚀、膨胀及边缘检测算子可提取纸张图像中的纸病边缘，结合传统的图像阈值分割方法能实现良好的纸病边缘检测效果。

[1]关健华.全幅纸病检测技术及在造纸中的应用[J].中国造纸，2000，19（6）：32-35.

[2]吕岑，张根宝，孙瑜.纸病图像的数学形态学分割方法[J].山西科技大学学报，2003，21（6）：82-85.

[3]韩培友.IDL可视化分析与应用[M].陕西，西北工业大学出版社，2006.

[4]章毓晋.图像分析[M].北京，清华大学出版社，2005：367-368.

2011－9－28

造纸化学品