地震动峰值速度对地下隧洞内力的影响研究1

尤红兵 张郁山 赵凤新

（中国地震灾害防御中心，北京100029）

地震动峰值速度对地下隧洞内力的影响研究1

尤红兵 张郁山 赵凤新

（中国地震灾害防御中心，北京100029）

本文利用混合模拟方法，合成了加速度反应谱及峰值位移相同，而峰值速度不同的两组人工地震动时程。同时选择典型隧洞，进行了弹塑性地震反应分析，研究了地震波水平输入时，地震动峰值速度对隧洞内力的影响。在软土场地中，当加速度反应谱及峰值位移相同时，峰值速度较大的地震动时程将引起隧洞较大的弯矩和剪力。在硬土场地中，峰值速度对隧洞弯矩和剪力的影响较复杂，没有明显规律，某些单元的弯矩和剪力可能会明显增大。峰值速度对隧洞单元轴力的影响较小。在进行地下隧洞设计的地震动参数确定时，应合理考虑峰值速度的影响。

人造地震动 峰值速度 隧洞内力 地震反应 内力

引言

近年来，我国的地铁建设得到了迅猛的发展，很多地铁工程建设在高烈度地区，其抗震问题越来越受到重视，相关研究正逐步深入。如何选用合适的地震波作为研究的地震动输入，一直是学者们关注的重要课题。在地震强度和震中距相同的条件下，地下结构的震害程度可能取决于峰值加速度和峰值速度（Hashash等，2001）。合理确定输入地震动，研究地震动峰值速度对地下隧洞地震反应的影响，具有重要的理论意义和实际应用价值。

在选用地震波时，一般根据地震动三要素进行选取或人工合成，并根据需要做适当调整。许多学者采用El-Centro波、Loma Prieta波、宁河天津波等天然地震波或人工合成波研究了地下结构的动力响应规律（陈国兴等，2004；庄海洋，2006；谷拴成等，2006；于品清，2009；蒋英礼，2009）。高学奎等（2005）根据加速度反应谱值平台段的均值、峰值速度（PGV）与峰值加速度（PGA）的比值选择地震波，认为较大 PGV/PGA 比值的近场地震波会引起结构较大的地震响应。这些研究在选用地震波时，综合考虑了峰值加速度、PGV/PGA 比值、频谱等多种地震动特性对结构的影响，但无法单独考虑峰值速度对结构地震反应的影响。

近年来，赵凤新和张郁山（2006a；2006b；2007）提出了新的地震动合成方法，实现了对绝对加速度反应谱和峰值速度、峰值位移的拟合，为相关研究的开展创造了条件。周媛（2006）利用加速度反应谱一致而峰值速度、峰值位移不同的人工时程，研究了地震动速度与位移对大跨斜拉桥地震反应的影响，推进了地震动峰值特性对结构地震反应影响规律的研究。

本文以绝对加速度反应谱和峰值速度、峰值位移为目标，通过在时域内叠加窄带时程，合成两组人造地震动时程。同时选择典型隧洞，进行弹塑性地震反应分析，研究了地震动峰值速度对隧洞内力的影响，为地下工程设计地震动参数的确定提供了参考。

1 人工地震动合成

以绝对加速度反应谱和峰值速度、峰值位移为目标，首先利用在传统的频域内调整傅立叶幅值谱的方法，生成以给定峰值加速度、反应谱和强度包线为目标的初始加速度时程；然后利用在时域内叠加窄带时程的方法来进一步调整，对目标峰值速度、峰值位移进行拟合。这种混合模拟方法对目标反应谱和目标峰值速度、峰值位移的拟合具有很高的精度（赵凤新等，2006a；2006b；2007）。

目标加速度反应谱的选取参照《建筑抗震设计规范（GB 50011-2001）》（2008年修订版）（中华人民共和国国家标准，2008）第5.1.5条规定的地震影响曲线，峰值加速度（PGA）取0.1g；特征周期Tg根据表5.1.4-2取值：场地类别为Ⅱ类，设计地震动分为两组，即Tg= 0.40s；阻尼比ζ = 0.05。

利用混合模拟方法，合成加速度反应谱及峰值位移（PGD）相同，而峰值速度（PGV）不同的两组人工地震动时程，每组时程有10个样本；同一组的10个样本时程的加速度反应谱、PGV、PGD均相同。第II组时程的PGV为第I组时程PGV的2倍，如表1所示。利用这两组时程，研究峰值速度对地下结构地震反应的影响。从每组10个样本中任选2条时程，第I组时程为I-1、I-2，第II组为II-1、II-2，其加速度、速度、位移时程如图1、图2所示。图中a、v、d分别表示加速度、速度、位移；t表示时间。加速度反应谱与目标规范反应谱的比较如图3所示。所有人工地震动时程的平稳段为8.0s，平稳段的起止时刻为3.0s和11.0s。所有样本的反应谱、峰值速度、峰值位移与目标值之间的相对误差均在5%之内。

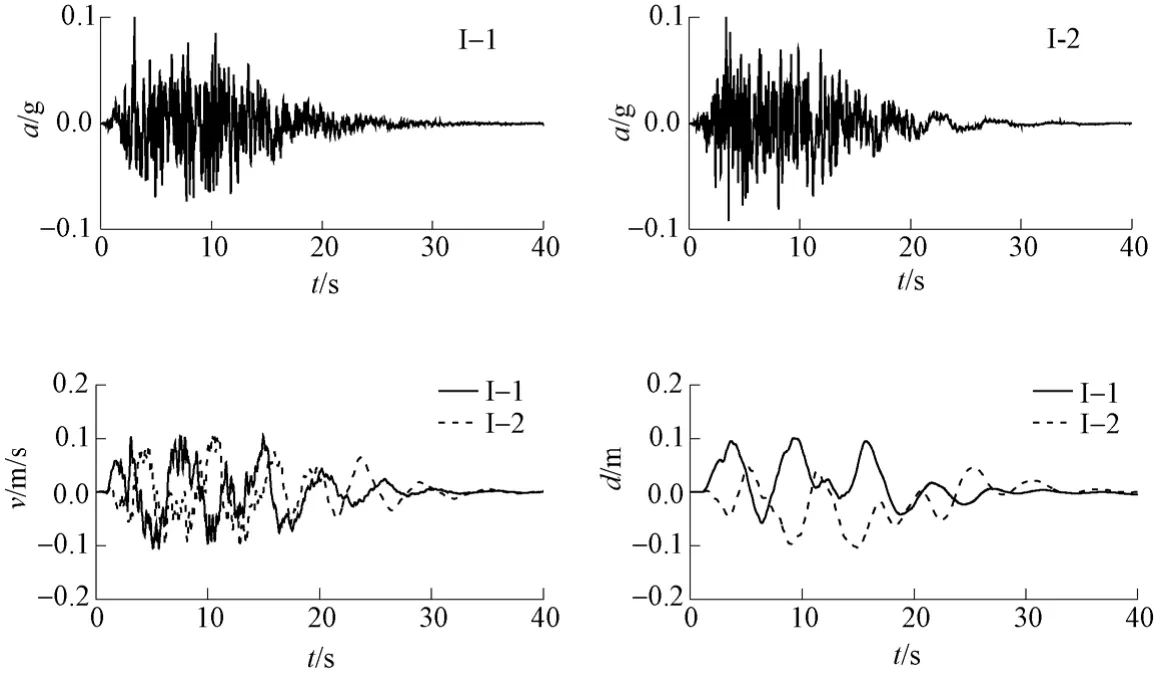
图1 第I组人工地震动时程Fig. 1 Artificial time histories of group I

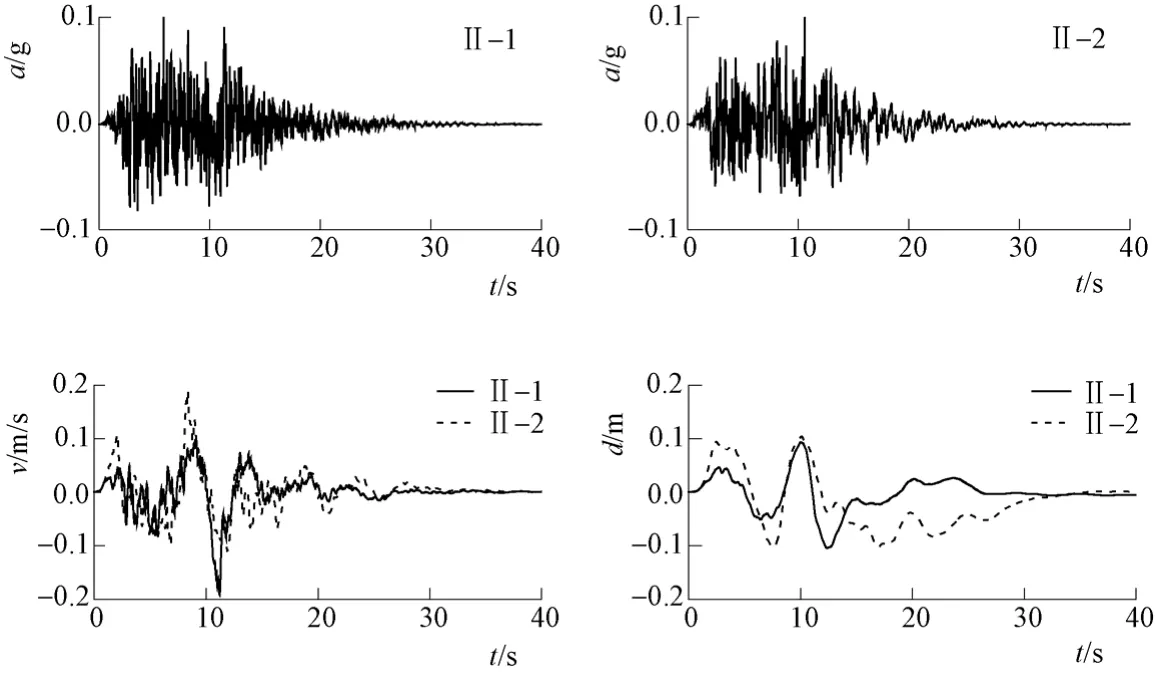
图2 第II组人工地震动时程Fig. 2 Artificial time histories of group II

表1 地震动时程的峰值Table 1 Peak values of artificial ground motions

表2 场地计算参数Table 2 Parameters of the sites

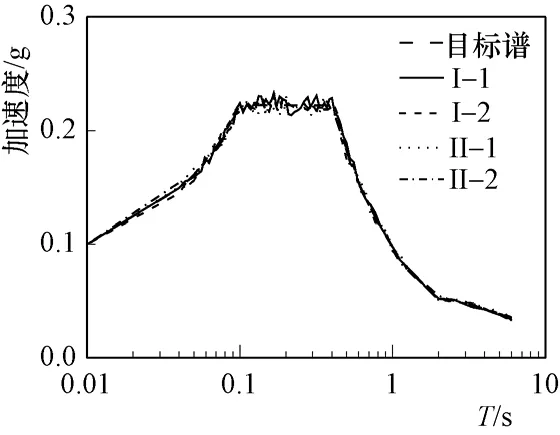
图3 目标谱及各人工时程反应谱比较Fig. 3 Comparison of the target spectrum and the response spectra of artificial ground motions

图4 隧洞单元划分及编号Fig. 4 The element mesh and serial number of tunnel

图5 土-隧洞相互作用体系有限元模型Fig. 5 The analytic model of soil-tunnel interaction system

2 隧洞及场地计算模型

建立计算模型时，假定土体为横向均质土体，衬砌结构沿隧洞纵向为无限长的结构体，简化为二维平面应变问题进行分析。隧洞采用混凝土管片拼装而成的环形衬砌结构，区间隧洞的内径为5.5m，外径为6.2m，壁厚为0.35m，隧洞管片采用C50混凝土，隧洞埋深8.0m。场地取基岩上单一均匀土层，厚度为50m。土体的本构模型采用摩尔-库仑模型，场地A、场地B的计算参数如表2所示。隧洞混凝土衬砌的弹性模量取34500 MPa，密度为2500kg/m3，泊松比为0.2。

根据隧洞尺寸，模型水平方向计算宽度取为110m。隧洞混凝土衬砌采用FLAC中的beam单元模拟，本构模型为线弹性模型。隧洞衬砌划分为 48个单元，其单元划分及编号如图 4所示。土-隧洞相互作用体系整体网格划分如图5所示，根据有限差分法计算波动问题的网格划分原则，在进行网格划分时，对应力应变复杂的衬砌结构周围土体采用均匀密集的网格进行划分，对远离衬砌结构的土体网格密度逐渐放大，最小网格尺寸为 0.5m，最大为 1.5m。衬砌单元与土体网格直接相联，未考虑隧洞结构与地基土之间的相对滑移和摩擦。阻尼采用瑞利阻尼，土的阻尼比取 5%，采用场地的自振频率作为瑞利阻尼的中心频率。以人工合成的两组地震动为基岩输入时程，从模型底部水平输入，场地两侧采用FLAC中的自由场边界模拟无限场地。

3 结果分析

首先进行静力分析，静力荷载包括重力和地面荷载，计算中场地上覆地表压力取为20kPa。将静力结果作为初始条件，进行动力分析。水平输入加速度时程峰值Amax分别调整为0.1g、0.2g、0.3g。加速度峰值调整后，峰值速度、峰值位移也将相应变化。与0.1g相比，当Amax调整为0.2g时，各组时程的峰值速度、峰值位移均增大1倍。在不同地震输入下，分别得到了地下隧洞的地震反应，分析输入地震动峰值速度对隧洞衬砌内力的影响。

3.1 对隧洞弯矩的影响

当输入加速度时程分别为I-2、II-1，且加速度峰值为0.1g时，场地A隧洞第19单元的弯矩时程如图6所示。选取所有单元弯矩时程的绝对值最大值，得到在I-2或II-1输入下场地A隧洞各单元弯矩最大值随单元编号的变化曲线。同样可得到其他输入时程下，场地A隧洞各单元弯矩最大值随单元编号的变化曲线，如图7中虚线所示。图中，实线为每组各单元10个结果的平均值。采用同样方法得到加速度峰值为0.2g、0.3g时，各单元的每组平均弯矩值，如图8所示。

图6 隧洞第19单元弯矩时程（场地A）Fig. 6 Time histories of tunnel moment for the 19th element (Site A)

图7 隧洞各单元弯矩最大值及各组平均弯矩（场地A）Fig.7 The maximum moment of each tunnel element and the average moment of each group (Site A)

图8分别给出了场地A、场地B中隧洞在第I、第II组时程输入下，隧洞衬砌各单元的每组平均弯矩值。图中，0.1g、0.2g、0.3g表示输入加速度时程的峰值。为方便比较，图 9给出了隧洞衬砌各单元每组平均弯矩值的相对变化。图中MI-II=( MII-MI)/ MI×100%，MI、MII分别表示在第I、第II组时程输入下各单元的每组平均弯矩值。

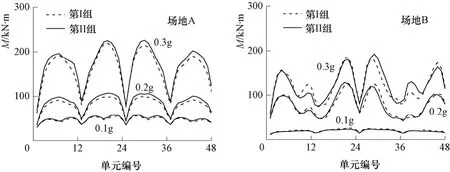
图8 隧洞衬砌各单元每组平均弯矩Fig. 8 The average moment of each group

从图8和图9可以看出，当输入加速度幅值较小时，峰值速度对隧洞衬砌单元弯矩的影响较小；当输入加速度幅值较大时，峰值速度对隧洞衬砌单元弯矩的影响也较大。对于场地A，MI-II最大值分别为：7.34%（0.1g）、10.4%（0.2g）、14.9%（0.3g）。这主要是因为当输入加速度幅值较小时，土体的塑性变形较小，接近于弹性情况。当输入加速度反应谱相同时，峰值速度对弹性反应影响很小。当输入加速度幅值较大时，土体的塑性变形也较大，峰值速度对隧洞地震反应的影响也增大。

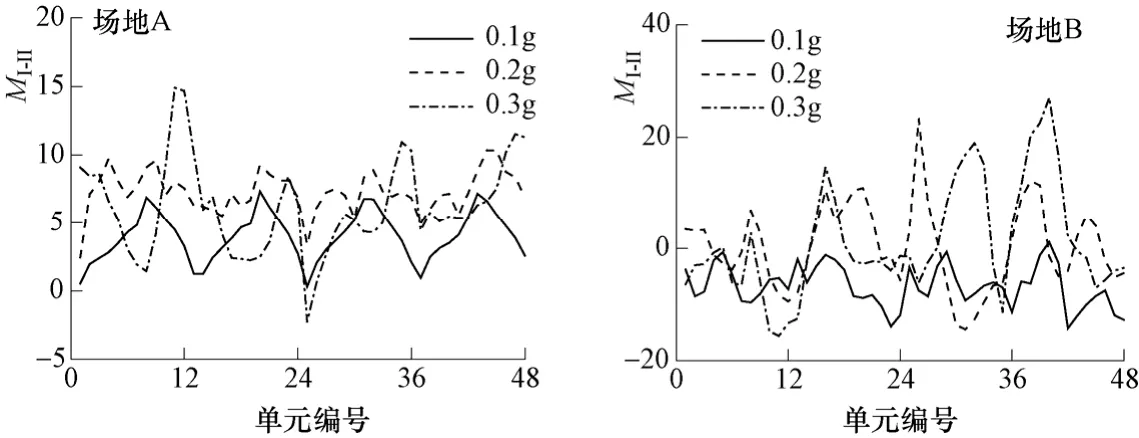
图9 隧洞衬砌各单元每组平均弯矩的相对变化Fig. 9 The relative change of average moment of each group for every tunnel element

在不同的场地条件下，峰值速度对隧洞弯矩的影响程度也不同。场地A为软土场地，除个别单元外（0.3g，第25单元，MI-II= -2.26%），其余单元第II组的平均弯矩均大于第I组的相应结果（见图8、图9）。如当输入加速度幅值为0.3g时，第11单元第I组的平均弯矩为150.2kN·m，第II组的平均弯矩为172.6kN·m，增大了14.9%。场地B为硬土场地，两组单元弯矩的变化较复杂，没有明显规律（见图 8、图 9）。如当输入加速度幅值为 0.3g时，第11单元第I组的平均弯矩为124.6kN·m，第II组的平均弯矩为105.2kN·m，减小了15.6%；第40单元第I组的平均弯矩为96.7kN·m，第II组的平均弯矩为122.9kN·m，增大了27.1%。说明在软土场地中，当加速度反应谱及峰值位移相同时，峰值速度较大的地震动时程将引起隧洞较大的弯矩。在硬土场地中，峰值速度较大的地震动时程会引起隧洞某些单元的弯矩出现明显的增大或减小。

3.2 对隧洞剪力的影响

采用与弯矩相同的处理方法，通过隧洞衬砌单元的剪力时程（图 10），得到隧洞各单元剪力最大值随单元编号的变化曲线，如图11中虚线所示。在不同输入加速度幅值下，将每组10个结果平均，得到隧洞衬砌各单元每组平均剪力，如图12所示。为方便比较，图13给出了隧洞衬砌各单元每组平均剪力的相对变化。图中QI-II=(QII-QI)/ QI×100%，QI、QII分别表示在第I、第II组时程输入下各单元的每组平均剪力。

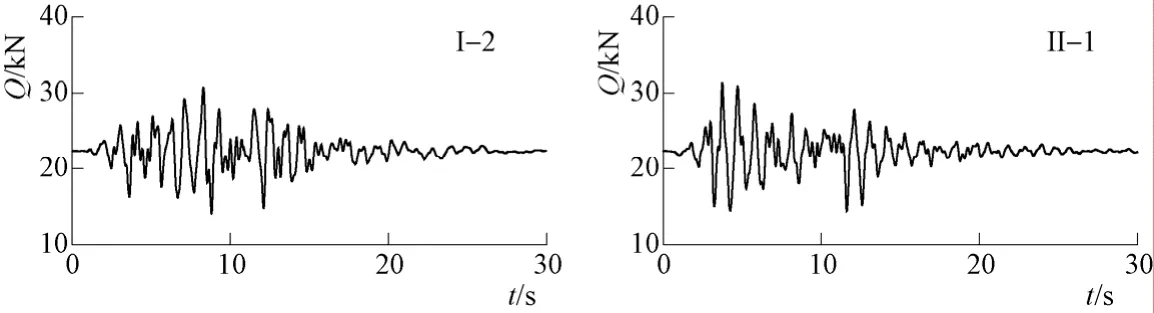
图10 隧洞第31单元剪力时程（场地A）Fig. 10 Time histories of shear force for the 31st element（Site A）

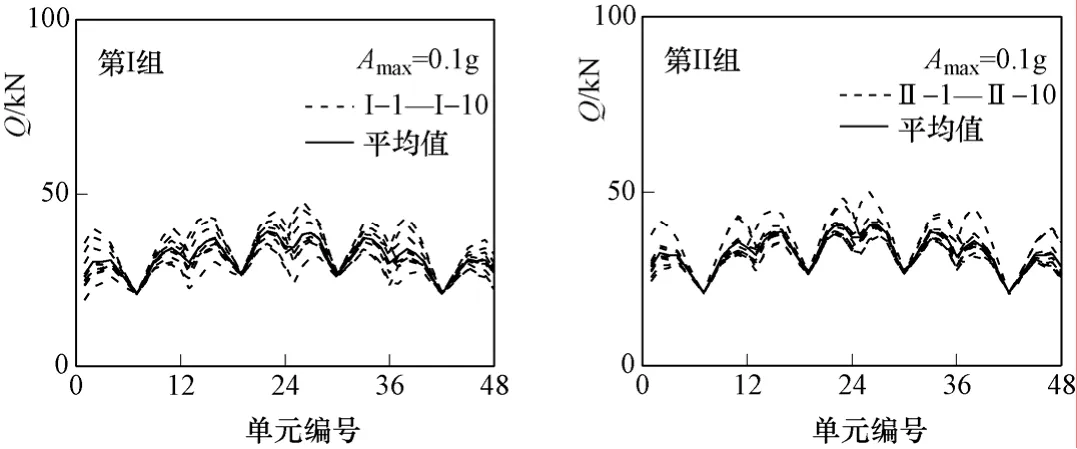
图11 隧洞各单元剪力最大值及各组平均剪力（场地A）Fig. 11 The maximum shear force of every tunnel element and the average shear force of each group (Site A)

图12 隧洞衬砌各单元每组平均剪力Fig. 12 The average shear force of each group for every tunnel element

峰值速度对隧洞剪力的影响规律与对弯矩的影响类似。从图12和图13可以看出，当输入加速度幅值较小时，峰值速度对隧洞衬砌单元剪力的影响较小；当输入加速度幅值较大时，峰值速度对隧洞衬砌单元剪力的影响也较大。对于场地A，QI-II最大值分别为：7.5%（0.1g）、12.6%（0.2g）、18.4%（0.3g）。峰值速度对线性反应影响很小，但对非线性反应有明显影响。

对于场地A，除个别单元外，大部分单元第II组的平均剪力均大于第I组的相应结果（见图12、图13）。如当输入加速度幅值为0.3g时，第42单元第II组的平均剪力比第I组的平均值增大了18.4%。另一方面，当输入加速度幅值为0.2g时，第I组的平均剪力最大值为79.2kN（第24单元），第II组的平均剪力最大为86.1kN（第25单元），与第I组的最大值相比增大了8.7%。说明在软土场地中，当加速度反应谱及峰值位移相同时，峰值速度较大的地震动时程将引起隧洞较大的剪力。

对于场地B，两组单元剪力的变化较复杂，没有明显规律（见图12、图13）。在硬土场地中，峰值速度较大的地震动时程会引起隧洞某些单元的剪力出现明显的增大或减小，但对所有单元中剪力最大值的影响较小。如当输入加速度幅值为0.2g时，第22单元第I组的平均剪力为81.6kN，第II组的平均剪力为107.8kN，增大了32.1%；第27单元第I组的平均剪力为95.1kN，第II组的平均剪力为75.8kN，减小了20.2%。另一方面，当输入加速度幅值为0.3g时，第I组的平均剪力最大值为167.7kN（第24单元），第II组的平均剪力最大值为168.7kN（第24单元），只增大了0.6%。

3.3 对隧洞轴力的影响

采用与弯矩相同的处理方法，通过隧洞衬砌单元的轴力时程（图 14），得到隧洞各单元轴力最大值随单元编号的变化曲线，如图15中虚线所示。在不同输入加速度幅值下，将每组10个结果平均，得到隧洞衬砌各单元每组平均轴力，如图16所示。为方便比较，图17给出了隧洞衬砌各单元每组平均轴力的相对变化。图中NI-II=(NII-NI)/NI×100%，NI、NII分别表示在第I、第II组时程输入下各单元的每组平均轴力。

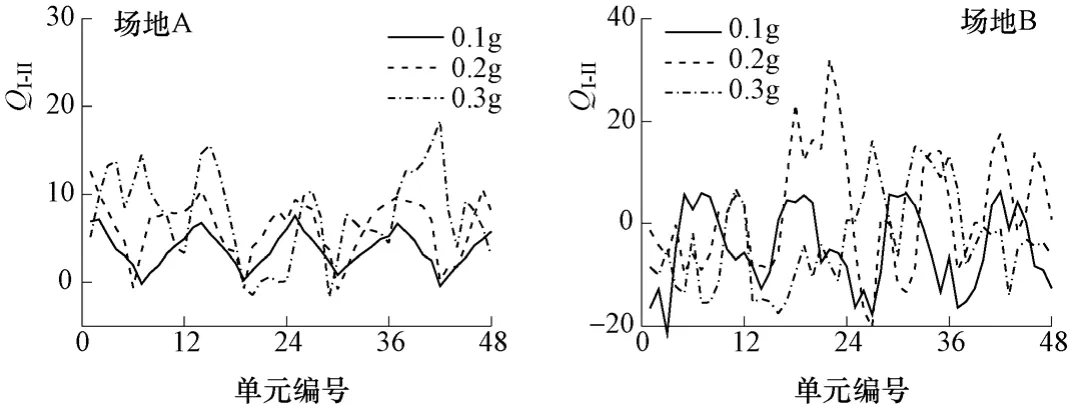
图13 隧洞衬砌各单元每组平均剪力的相对变化Fig. 13 The relative change of average shear force of each group for every tunnel element

图14 隧洞第19单元轴力时程（场地A）Fig. 14 Time histories of axial force for the 19th element (Site A)

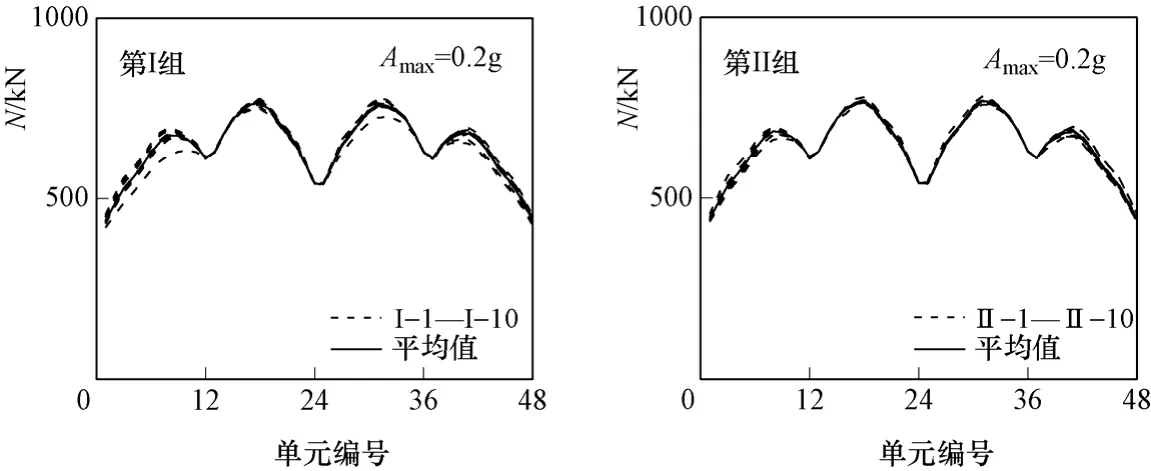
图15 隧洞各单元弯矩最大值及各组平均轴力（场地A）Fig. 15 The maximum axial force of every tunnel element and the average axial force of each group (Site A)

从图16和图17可以看出：当地震波水平输入时，峰值速度对隧洞衬砌单元轴力的影响较小。在两组结果中，同一单元的轴力增大或减小的幅度一般不超过 5%。对于场地 A，当输入加速度幅值为0.3g时，第I组的平均轴力最大为807.3kN（第18单元），第II组的平均轴力最大为807.2kN（第31单元），几乎相等。对于场地B，当输入加速度幅值为0.3g时，第I组的平均轴力最大为895.9kN（第29单元），第II组的平均轴力最大为897.2kN（第30单元），只增大了0.1%。

图16 隧洞衬砌各单元每组平均轴力Fig. 16 The average axial force of each group for every tunnel element

图17 隧洞衬砌各单元每组平均轴力的相对变化Fig. 17 The relative change of average axial force of each group for every tunnel element

4 结语

以绝对加速度反应谱和峰值速度、峰值位移为目标，通过在时域内叠加窄带时程，合成了目标加速度反应谱及峰值位移相同，而峰值速度不同的两组人工地震动时程。选择典型隧洞，进行了弹塑性地震反应分析，研究了地震动峰值速度对隧洞内力的影响，研究表明：

（1）当水平输入加速度幅值较小时，土体的塑性变形较小，接近于弹性情况，峰值速度对隧洞衬砌单元内力的影响较小；当水平输入加速度幅值较大时，土体的塑性变形也较大，峰值速度对隧洞衬砌单元弯矩、剪力的影响也较大。

（2）在软土场地中，当加速度反应谱及峰值位移相同时，峰值速度较大的地震动时程将引起隧洞较大的弯矩和剪力。

（3）在硬土场地中，峰值速度对隧洞弯矩和剪力的影响较复杂，没有明显规律。某些单元的弯矩和剪力可能会明显增大或减小。

（4）当地震波水平输入时，峰值速度对隧洞单元轴力的影响较小。在两组结果中，同一单元轴力的相对变化一般不超过5%，而所有单元轴力的最大值相差均不超过1%。

（5）在地下工程设计地震动参数确定或选择输入地震波时，应重视峰值速度的影响。

本文在进行土-隧洞相互作用的地震反应分析时，并未考虑隧洞衬砌结构与土体之间的接触非线性，这使隧洞的非线性地震反应分析结果有一定的局限性，在今后的研究中还需做进一步的补充。限于篇幅，在水平及竖向地震作用下，峰值速度对隧洞内力地震反应的影响将另文讨论。

陈国兴，庄海洋，徐烨，2004. 软弱地基浅埋隧洞对场地设计地震动的影响. 岩土工程学报，26（6）：739—744.

高学奎，朱唏，2005. 近场地震动输入问题的研究. 华北科技学院学报，2（3）：80—83.

谷拴成，朱彬，杨鹏，2006. 地下结构地震反应非线性分析. 地下空间与工程学报，2（5）：748—752.

蒋英礼，2009. 软土地铁车站地震作用下的响应分析 [硕士学位论文]. 北京：北京交通大学.

于品清，2009. 软土地下结构地震反应及其环境影响评价 [硕士学位论文]. 大连：大连理工大学.

赵凤新，张郁山，2006a. 拟合峰值速度与目标反应谱的人造地震动. 地震学报，28（4）：429—437.

赵凤新，张郁山，2007. 拟合峰值位移与目标反应谱的人造地震动. 核动力工程，28（2）：38—41.

庄海洋，2006. 土-地下结构非线性动力相互作用及其大型振动台试验研究 [博士学位论文]. 南京：南京工业大学.

周媛，2006. 地震动速度与位移对大跨斜拉桥地震反应影响的研究 [硕士学位论文]. 北京：中国地震局地球物理研究所.

中华人民共和国国家标准，2008.《建筑抗震设计规范（GB50011-2001）》（2008年修订版）. 北京：中国建筑工业出版社.

Hashash Y.M.A., Hook J.J., Schmidt B., 2001. Seismic design and analysis of underground structures. Tunneling and Underground Space Technology, 16 (6): 247—293.

Zhao Fengxin, Zhang Yushan, Lu Hongshan, 2006b. Artificial ground motion compatible with specified ground shaking peaks and target response spectrum. Earthquake Engineering and Engineering Vibration, 5 (1): 41—48.

Influence of Peak Ground Velocity on the Internal Force of Underground Tunnel

You Hongbing, Zhang Yushan and Zhao Fengxin
( China Earthquake Disaster Prevention Center, Beijing 100029, China)

A hybrid simulation method is used to generate two group artificial ground motions that are compatible with the same response spectrum of absolute acceleration and same peak displacement, but different peak velocities. The elastic-plastic seismic response analyses of underground tunnel are performed. The influence of peak ground velocity (PGV) on the internal force of underground tunnel are studied. For the time histories with the same response spectrum and same peak displacement, the larger PGV will cause the larger moment and shear force for the underground tunnel in soft soil site. The influence of PGV on the moment and shear force of the tunnel in stiff soil site is irregular. The moment and shear force of some tunnel elements can be increased obviously. The PGV has less effect on the axial force of the underground tunnel. The influence of peak velocity should be considered reasonably in determination of design ground motion parameters for underground tunnels.

Artificial ground motion; PGV; Underground tunnel; Seismic response; Internal force

尤红兵，张郁山，赵凤新，2011. 地震动峰值速度对地下隧洞内力的影响研究. 震灾防御技术，6（2）：105—115.

地震科学基金（编号A08109）资助

2010-12-16

尤红兵，男，生于1970年。副研究员。主要研究领域：地震工程。E-mail: hbyou@126.com