基于交叉口冲突消除的区域疏散交通管理研究——以长春市中心区疏散交通管理为例
安 实,王 泽,崔建勋,王 健
(哈尔滨工业大学交通安全特种材料与智能化控制技术交通行业重点实验室,哈尔滨 150090)
基于交叉口冲突消除的区域疏散交通管理研究
——以长春市中心区疏散交通管理为例
安 实,王 泽,崔建勋,王 健
(哈尔滨工业大学交通安全特种材料与智能化控制技术交通行业重点实验室,哈尔滨 150090)
针对非常规突发事件下区域大规模机动车辆疏散的交通运行管理进行了研究。以元胞传输模型为理论基础,针对疏散交通流时空分布的高度随机、动态特性,建立了区域疏散系统最优动态交通分配模型。进一步重点分析了平面交叉口在疏散过程中的瓶颈问题,整合了交叉口流向冲突消除的交通管理策略,构建了基于交叉口冲突消除的疏散交通管理优化模型。最后以长春市中心区路网和2020年人口预测数据为依托进行实证分析,结果表明该模型能够为疏散交通管理者的决策提供有效支撑。
区域疏散管理;元胞传输模型;动态交通分配;交叉口冲突消除
常态交通系统运行管理中,平面交叉口信号控制通过时间上分离冲突的交通流以保证车流运行秩序,提高道路网上的人车物的运输效率。由于紧急疏散情形下,短时内疏散交通需求较大,关键交叉口的交通流受到的轻微扰动,极易产生大范围的交通拥堵,造成区域疏散的极大延误;其次,紧急状态下交叉口各流向的交通需求波动性较大,难以有效进行预测,导致难以制定合理、有利于全局疏散效率最大化的交叉口信号控制方案;再次,驾驶员由于逃生的紧迫性,往往在交叉口处表现出缺乏耐心,极易违章闯红灯行驶,极大降低了交叉口的通行效率和交通安全。科学合理的应急交通管理方案,是完成大规模机动车疏散的重要前提,因此,如何制定疏散情形下交叉口冲突消除策略,是提高疏散效率、保证人民生命财产安全的重要方面。
疏散策略制定的理论基础在于对疏散者行为和疏散交通流特性的把握。目前,国内外学者针对灾害所导致的大规模区域疏散问题的研究,所采用的建模方法大致分为,网络流理论、交通分配理论和基于简单路径选择规则的计算机仿真方法[1~4]。然而,研究的核心瓶颈在于所建模型存在过多理想的假设,不能有效地刻画疏散者行为与疏散交通流的动态、随机特性,因而无法给出合理、实用的疏散交通管理方案[5]。同时,当前多数研究均是在疏散交通规划的层面,评价不同疏散交通应急管理策略的疏散性能(主要衡量指标为疏散清空时间),和制定合理的道路交通应急疏散预案,而服务于疏散交通管理与控制实践层面的研究较为匮乏。
本文研究以 Daganzo(1994)[6]提出的元胞传输模型(Cell Transmission Model,CTM)模型为重要理论基础,由于该模型能够捕捉到网络交通流中的不连续变化现象,较好地模拟出激波、排队形成、排队消散以及多路段间的相互影响等交通动力学特性,将其应用于疏散动态交通分配中,以增强估算路径阻抗的准确性,提高疏散动态交通分配模型的应用效果[7]。在假定疏散情景(路网、车辆和待疏散人口以及要求的疏散清空时间等)确定的情况下,着重针对区域疏散过程中的动态路径分配以及平面交叉口交通流向冲突消除进行整合研究,对疏散交通流的描述能够恰当反映疏散过程中所形成的排队、交叉口交通特性以及事故等非常态下的交通流特征,能够为疏散交通管理者提供最优的疏散交通管理决策支持。
一、区域疏散系统最优动态交通分配模型
区域疏散系统最优动态交通分配模型是疏散交叉口冲突消除策略制定的重要基础,疏散交通分配的过程就是对交通流时空分布规律的捕捉和刻画。本节将假定个体出行者服从系统管理者的调度和指挥,按照系统最优的目标进行疏散,以CTM理论为基础,构建系统最优的区域疏散动态交通分配模型。
(一)元胞传输模型(CTM)理论基础
CTM本质上属于时空离散的动力学系统。首先,在空间上路段被离散化为一系列等长的、相互邻接的同质小段,称为元胞(cell)。其次,时间上,CTM将交通流动态的考察时间周期离散化为多个单位时间间隔,允许根据问题精度进行间隔大小自定义(时间间隔越小,模型的精度越高,但求解性能越低)。再次,每个元胞具有其特定的状态,即某个单位时间间隔内存在的车辆数。这样,在时空离散所构造的二维空间内,每个元胞依据其上游和下游元胞的状态,不断地更新自身的状态,从而模拟交通流的时空演变规律。
如前所述,任意元胞 i∈□(□为元胞集合),在任意时间间隔[t,t+1]内都具有自身的状态,即t时刻开始时,其上存在的车辆数,xti。元胞i的状态,将在研究的时间范围内,不断的依据相邻元胞状态(∀δ与 i相邻)进行自身状态更新。依据流量守恒,可得元胞状态更新公式,如式(1):

式中,Ψ-(i),Ψ(i)分别为元胞i的上游邻接元胞集合和下游邻接元胞集合为间隔[t,t+1]内,由元胞i流入到元胞j的车流量为间隔[t,t+1]内,元胞i处产生的车辆数。

(二)基于CTM的区域疏散系统最优动态交通分配模型
1.目标函数
疏散交通动态分配的目标是使得疏散系统的总出行时间最小,系统的总出行时间可以表达为:

式(4)的含义为,疏散问题的研究时间区域Ω =[0,1,2,…,T]被离散化为 T 个等长的小时段τ,疏散的元胞模型系统便是以为单位时间阶进行状态演化(如图1所示)。任意单位时段[t,t+1],(t,t+1∈Ω 内,系统中除已到达疏散终点元胞(□p)的车辆以外,其余每辆车的出行时间或原地停留时间即为单位时间间隔。由此可知,在研究时间区域Ω=[0,1,2,…,T]内,系统的总出行时间可表述为:所有单位时间间隔τ内,除虚拟终点元胞(□p)以外的全部元胞上的车辆数与单位时间间隔τ的乘积之和,如式(4)所示。

图1 系统时钟的推进
由于目标函数中,单位时间间隔τ为一个常量,因而可以在目标函数中将其去除,这样目标函数可以表达为式(5):

2.约束条件
第一,流量守恒约束。对任意元胞i∈□,任意[t,t+1]小时段而言,t+1 时刻的车辆数应等于t时刻时的车辆数加上该时段内流入元胞i的车辆数以及该时段内该元胞处所产生的车辆需求,并减去该时段内从元胞i流出的车辆数,即:

第二,流量传播约束。车辆输出约束:在任意[t,t+1]小时段内,对任意元胞 i∈□而言,其输出的全部车辆数应不超过其所能输出的最大车辆数;而其所能输出的最大车辆数一定不超过该元胞在t时刻其上所拥有的车辆数与t时刻其单位时间间隔内的最大流率)两者之中的最小者,即

车辆输入约束:在任意[t,t+1]小时段内,对任意元胞i∈□而言,流入其的全部车辆数)应不超过其所能接收的最大车辆数);而其所能接收的最大车辆数一定不超过该元胞在时刻其上所剩余的“空间与t时刻其单位时间间隔内的最大流率两者之中的最小者,即:
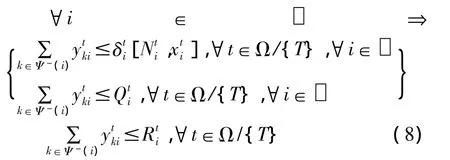
第三,产生—吸引平衡约束。在T时刻,疏散交通仿真结束,此时所有疏散起点元胞处产生的需求必须完全抵达疏散终点元胞p∈□p(假定给定的仿真时限足够疏散所有的交通需求),即:

第四,初始条件。在问题研究的初始时刻,令所有元胞上的车辆数为0,即:

第五,非负约束。

以此构造的疏散动态交通分配模型,其本质上属于线性规划模型,决策变量为和,因此模型的求解可以从系统最优的角度,确定任意一个小时间段内,任意元胞上的车辆数以及元胞之间的最佳流量。
二、基于交叉口冲突的区域疏散交通管理模型
城市平面交叉口把城市道路相互连接起来构成道路网,其通行能力制约着城市道路的通达,是影响道路畅通的瓶颈。解决好城市交叉口的交通控制管理,挖掘现有交通资源的潜力,提高紧急情形下交叉口短时疏散需求的通行能力,减少在交叉口处的停车与延误,提高疏散的安全性和快速性具有重要意义。本节提出了紧急疏散情况下交叉口冲突消除的交通组织方案,以期将平面交叉口转化为非间断流设施。图2描绘了一个标准的十字交叉口的冲突点,除去冲突点可以减少交叉口的延误和总的疏散时间,同时可以减少潜在的交叉口事故点。图2(a)中表示了在无交通组织措施的情况下交叉口的冲突点和交织点情况,可以看出该情况下存在着16个冲突点。图2(b)则通过在交叉口的两个入口道处设置路障,从而使交叉口的冲突点数减少到3。图2(c)进一步通过设置路障,消除了交叉口中的所有冲突点,但仍旧存在着交织点;图2(d)则通过路障的设置完全消除了交叉口的冲突点和交织点。消除交叉口冲突点的优势在于使得交叉口的交通流通行更加有序和安全,但却增加了疏散车辆的平均出行距离。
因而,交叉口冲突消除策略实施的核心问题在于,确定交叉口哪些流向可以通行,哪些流向禁止通行。为此,首先引入表征交叉口流向是否通行的二元指示变量πi,其定义如下:

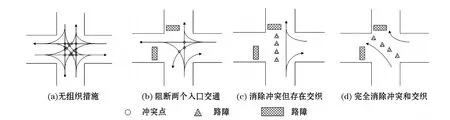
图2 十字交叉口处的各种交通组织方案
对于任意流向(i,j)∈χ而言,其自身的车流通行指示变量与任意与之交通流向相互冲突的流向指示变量之和,应小于等于1,这样就保证了,在互相冲突的两个交叉口流向上,只能有一个流向上通行车辆,即:

式中,Ψ(i,j)为某个交叉口处与流向(i,j)相互冲突的流向集合。
为了在流向指示变量π与交叉口连接桥流量y之间建立联系,引入了交叉口连接桥所代表的流向通行能力约束条件,表达为:

因而,该研究将式(13)和(14)所代表的约束条件整合到前文提到的疏散交通分配模型中,由此得到了本质上属于混合整数规划的疏散交通管理模型。其决策变量为和 πij。因此模型的求解可以从系统最优的角度,确定任意一个小时间段内,任意元胞上的车辆数、元胞之间连接桥的最佳流量以及交叉口各流向是否允许通行。
三、长春市中心区疏散交通管理实证研究
长春市位于中国东北地区辽宁、吉林、黑龙江、内蒙古四省区通衢的十字要冲,是吉林省政治、经济、文化中心,是东北地区重要的交通枢纽和物流中心,也是中国北方区域性中心城市之一。近年来,长春社会经济发展迅速,综合实力增强,交通需求不断增长,按照国家和吉林省的工作要求已经逐步将城市应急管理列为重要日程,也充分意识到交通管理在新时期公共安全事件的关键作用。由于当前长春市交通供需的不平衡,很大程度上加剧了城市道路交通应急管理任务的艰巨性。本节实证数据取自于2008年哈尔滨工业大学承担的“长春城市道路网交通调查分析及快速路体系交通需求预测”项目,该项目是受长春市城乡建设委员会委托,哈尔滨工业大学联合长春市公安局交警支队、国家统计局长春市城调队、长春市民政局、吉林建筑工程学院等多家单位配合完成。下面以长春市南关区局部道路网为例,在长春市2020年远景交通规划的背景下,针对其城市应急管理中核心的理论问题进行研究,旨在从道路交通的角度,对长春市应急疏散交通管理进行实证研究,从而验证本文所建立模型的有效性。
(一)基础数据
1.路网数据
本文选取长春市南关区局部路网,如图3所示。
第一,路段数据。图3中所包含的吉林大路、自由大路、人民大街、南湖大路、临河街以及卫星路,均为长春市城区的主干道路。在2008年4—5月的调查期间,针对图3所示的长春市主要路段进行了基础数据和交通流量数据的采集。依据项目调查结果,表1给出了所得到的各路段基本数据。
第二,交叉口数据。图6所示的研究区域内包含了13个交叉口,除人民大街与卫星路交叉口(编号为11)为平面环形交叉口外,其余均为普通的信号控制平面交叉口。本文拟定10和11号交叉口所研究区域疏散问题中的避难所(即疏散终点)。
2.疏散问题的时间域及元胞—连接桥路网模型
疏散问题研究的时间域定义为30分钟,单位时间间隔分钟。依据表1所给出的路段基本数据,可以将图3所示的路网转化为图4所示的元胞—连接桥路网模型。其中,编号为1,2,3的元胞为疏散起点元胞,编号为70,71的元胞为疏散终点元胞,编号为72的元胞为虚拟终点元胞。图3中的元胞个数为72,连接桥个数为119。

表1 研究区域内路段的基本数据

图3 南关区局部路网

图4 元胞—连接桥路网模型
3.人口及车辆数据
在获取了研究区域内的路网基本数据后,需要明确所研究区域内的人口情况及相应的车辆使用情况,从而明确所研究区域疏散的交通需求。根据“项目”提供的2020年研究区域人口的预测数据,可以得到疏散的交通需求情况,如表2所示。

表2 2020年研究区域总疏散人口预测及车辆使用情况
4.疏散交通需求的动态加载
本文采用MASSVAC疏散交通规划软件中所采用的加载公式对每个交通小区的需求进行动态加载,其具体形式如式(15):
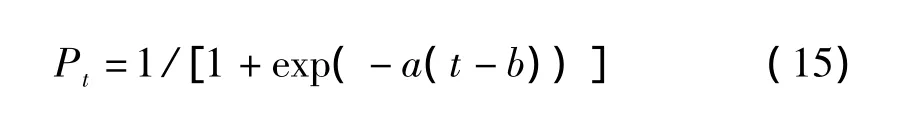
其中,Pt为t时刻疏散交通累计加载比例;a,b是可以调整的模型参数。其中a代表着公众对灾害的反应,可以通过它调整累计交通加载曲线的斜率,b为疏散交通加载总时间的一半。假定每个小区的全部疏散交通需求在疏散指令发布后(0时刻),10个单位时间间隔内全部加载到路网上,由此,本文的参数取值为:a=0.5,b=5。
(二)模型求解结果
基于以上数据,本文采用Matlab中Miprog()函数对模型进行了求解。求解结果:系统在30个时间间隔内,累积疏散机动车23613.9辆,其中疏散终点1累积疏散15175.7辆,疏散终点2累积疏散8438.2辆。图5给出了虚拟终点的累积车辆到达曲线。图6给出了研究区域内平面交叉口的流向冲突策略求解结果。

图5 虚拟终点累积车辆到达曲线
通过模型的求解,可以为决策者提供如下决策支持信息:
一是依据变量和的求解结果,可以帮助疏散管理者从系统最优的角度安排疏散者最佳逃生路径;二是根据求得的交叉口流向冲突消除结果,可以辅助确定交叉口处的警力、路障安排和布置;三是根据的求解结果,评估每个时段内,任意路段的交通运行态势。

图6 交叉口流向冲突消除求解结果
四、结论及展望
交通应急管理是典型的工管交叉问题,需要将工学理论和管理学方法综合考虑,本文研究如何在一定安全时限内,合理准确捕捉疏散交通流的时变特性,寻求疏散交通流实时管理策略的最佳配置,能够为道路交通应急管理者提供决策支持,以最大限度地减少疏散路网清空时间。本文基于CTM理论,构建了系统最优的疏散交通分配模型及基于交叉口冲突消除的疏散交通管理模型,并通过长春市2020年的疏散交通管理实证分析,验证了模型的有效性。通过该模型的求解不仅可以为管理者提供疏散者最佳逃生路径安排,同时可以提供交叉口流向管理以及路段交通流状态评估等信息及依据。
本文所建立的疏散交通管理模型本质上属于混合整数规划模型,在模型求解过程中,存在着大量的0—1决策变量,随着路网规模的扩大、离散时间间隔的增多,将使得最优化的求解难以实施。因而,在未来的研究中,应重点考察适用于大规模疏散交通分析的启发式算法设计。
[1]邹亮,任爱珠,张新.基于GIS的灾害疏散模拟及救援调度[J].自然灾害学报,2006,15(6):141-145.
[2]安实,崔建勋,王健.国外道路交通应急区域疏散综述[J].交通运输系统工程与信息,2008,8(6):38-45.
[3]COVA T J,JOHNSON J P.A Network Flow Model for Lane-based Evacuation Routing[J].Transportation Research Part A,2003,37:579-604.
[4]陈岳明,萧德云.应急疏散过程建模及其算法研究[J].交通运输系统工程与信息,2008,8(6):96-100.
[5]刘小明,胡红.应急交通疏散研究现状与展望[J].交通运输工程学报,2008,8(3):108-121.
[6]DAGANZO F C.The Cell Transmission Model:A Dynamic Representation of Highway traffic Consistent with the Hydrodynamic Theory[J].Transportation Research Part B,1994,28(4):269-287.
[7]LIU Y.Two-Level Integrated Optimization System for Planning of Emergency Evacuation[J].Journal of Transportation Engineering,2006,132(10):800 -807.
[责任编辑 王 春]
Research on Regional Evacuation Traffic Management Based on Crossing Elimination at Intersection—A Case Study in Downtown Changchun
AN Shi,WANG Ze,CUI Jian-xun,WANG Jian
(Key Laboratory of Advanced Materials& Intelligent Control Technology on Transportation Safety,Ministry of Communications,Harbin Institute of Technology,Harbin 150090,China)
This paper aims at the study of the regional evacuation traffic management of mass vehicles under unconventional emergencies.Based on the cell transmission model(CTM),this paper presents a system -optimum dynamic traffic assignment model which can effectively investigate the characteristics of randomness and dynamics of evacuation flowing spatial and temporal distribution.Furthermore,the bottleneck problem which often occurs at intersections during evacuation process is analyzed and an evacuation traffic management optimization model incorporating the crossing elimination strategy is presented.Combining the road network data and population prediction data in the 2020,this paper conducts an empirical study of evacuation traffic management at the central parts in Changchun city of China.The results show that this model can provide effective support for evacuation traffic managers’decision -making.
regional evacuation;cell transmission model;dynamic traffic assignment;crossing elimination
U 491
A
1009-1971(2011)05-0073-07
2011-09-28
国家自然科学基金资助项目“台风灾害条件下道路交通应急区域疏散建模与仿真研究”(70973032)
安实(1968-),男,黑龙江哈尔滨人,教授,博士生导师,从事交通应急管理与智能交通研究;王泽(1986-),女,山东黄县人,博士研究生,从事道路交通应急管理研究;崔建勋(1982-),男,黑龙江绥化人,博士后,从事道路交通应急管理研究;王健(1974-),男,安徽砀山人,教授,博士生导师,从事道路运输经济研究。

