航空重力向下延拓病态问题的求解
蒋 涛,李建成,王正涛,张守建
1.武汉大学测绘学院,湖北武汉430079;2.地球空间环境与大地测量教育部重点实验室,湖北武汉430079
航空重力向下延拓病态问题的求解
蒋 涛1,2,李建成1,2,王正涛1,2,张守建1,2
1.武汉大学测绘学院,湖北武汉430079;2.地球空间环境与大地测量教育部重点实验室,湖北武汉430079
提出将广义岭估计用于求解航空重力向下延拓病态问题。研究求解逆Poisson积分问题的三种正则化方法:Tikhonov正则化、岭估计和广义岭估计。利用EGM2008地球位模型设计模拟数值实验,将飞行高度处含白噪声的2.5′×2.5′重力扰动向下延拓至大地水准面上,与参考值作外部检验,全面检验、比较各向下延拓方法的可靠性、精度和稳定性。数值结果表明基于多个最优正则化参数的广义岭估计在延拓精度、稳定性和抗差性等方面表现良好。
航空重力;向下延拓;病态问题;正则化
1 引 言
随着全球定位系统(GPS)定位精度的提高、惯性导航系统(INS)和重力测量系统的改进,航空重力测量在5~10km的空间分辨率尺度上能够达到1~3mGal(1mGal=10-5m/s2)的数据精度,所提供的重力场中、短波信息与地面重力测量和卫星重力测量形成有效互补,特别是在地面重力测量难以达到的地区(如两极、森林和山区等),航空重力测量更是无可替代。航空重力测量观测值经过数据预处理,可得到飞行高度处的重力异常或重力扰动,但大地测量领域需要的是大地水准面上的重力值,因此需将飞行高度处的重力异常或重力扰动向下调和延拓至大地水准面上。
航空重力向下延拓是一个数据噪声放大的过程,属于病态问题,若不采用合适的延拓方法,将无法得到稳定可靠的重力延拓解。在现有重力向下延拓方法中,以求解球外Dirichlet问题的逆Poisson积分法应用最为广泛[1-6],其他方法还包括最小二乘配置(LSC)[7]、快速傅里叶变换(FFT)[8-9]、直接代表法[10]和求解球内Dirichlet问题的直接法[11-12]。逆Poisson积分法涉及求解Poisson积分方程,当数据点间隔较小或延拓高度较大时法方程呈病态,解算时需引入正则化处理。以往研究大多采用基于单个正则化参数的Tikhonov正则化或岭估计[4-6],而理论上基于多个最优正则化参数的广义岭估计所得估值具有比普通岭估计结果更小的平均均方误差[13],但目前尚未见到广义岭估计应用于重力向下延拓的研究结果发表,将基于广义岭估计的逆Poisson积分法用于向下延拓解算值得深入研究。本文以重力扰动为基本观测量,介绍了基于逆Poisson积分法求解航空重力向下延拓病态问题的数学模型,给出逆Poisson积分问题的三种正则化解法——Tikhonov正则化、岭估计和广义岭估计及确定正则化参数的详细算法,利用EGM2008重力位模型设计模拟数值试验全面比较分析了各正则化解法的可靠性、精度和稳定性。
2 数学模型
在球近似条件下,大地水准面可用半径为R的地心参考球表面近似表示(R=6 371km)。若已知大地水准面上的重力扰动δg(R,Ω′),求大地水准面外部空间某点的重力扰动δg(r,Ω),这一过程称为重力扰动的向上延拓,可通过求解以大地水准面为边界面、调和函数rδg所满足的球外Dirichlet问题实现[14]。向上延拓值表达为Poisson积分如下

式中,σ表示全球积分区域;(r,Ω)表示球坐标(r,φ,λ);K(r,ψ,R)表示Poisson积分核函数;L(r,ψ,R)表示点(r,Ω)与点(R,Ω′)之间的空间距离;ψ为两点地心方向间的球面距离;dΩ′为积分面元。重力扰动的向下延拓是已知大地水准面外部空间的δg(r,Ω),求解Poisson积分的逆问题,得到大地水准面上的δg(R,Ω′)。此时式(1)成为第一类Fredholm积分方程,点(r,Ω)为观测数据点,点(R,Ω′)为待求点,也可称为流动点。
理论上Poisson积分式(1)应在全球范围进行积分计算,但由于实际观测数据有限,一般将球面积分区域划分为近区和远区。近区是一个以数据点(r,Ω)为中心,ψ0为半径的球冠区域σ0;远区是球面上的剩余部分σ-σ0。Poisson核K(r,ψ,R)随着球面距离ψ增大而快速衰减。相对于近区流动点对数据点的贡献,远区流动点贡献的量级很小,可由位系数和Poisson核截断系数近似计算[1]

式中,Nf是所采用的位系数的最大阶数;a为参考椭球长半轴;¯Cnm、¯Snm为扰动位系数;¯Pnm(sinφ)为完全规格化勒让德函数;δgn(Ω)为重力扰动面球谐展开式;Qn(r,ψ0,R)为Poisson核截断系数。
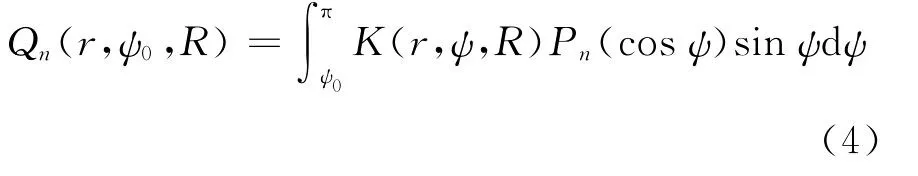
式(1)的离散形式如下
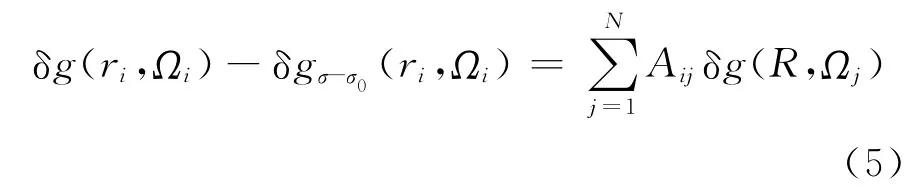
式中,i=1,2,…,M,M为观测数据点个数;N为待求点个数,M≥N;Aij为M×N阶设计矩阵A的元素。矩阵A的对角线元素为

A的非对角线元素为

式中,ΔΩj为第j个流动点所处格网的面积;Nc为处于球冠区σ0内的流动点个数。式(5)的解δg(R,Ωj)(j=1,2,…,N)即为大地水准面上的重力扰动延拓值。
3 正则化方法
向下延拓的观测方程(5)写成标准Gauss-Markov模型形式如下

式中,y为M阶观测值向量;A为M×N阶设计矩阵;x为N阶未知数向量;e为观测噪声,其数学期望为0;D{y}为观测值的方差-协方差阵;σ2是单位权方差;P是权阵,其最小二乘解为

向下延拓本质上是一个病态问题,延拓过程中会放大观测噪声和未模型化的信号。尽管将连续Poisson积分化为离散数值积分可在一定程度上抑制高频噪声,但随着数据格网间隔的减小和延拓高度的增加,设计矩阵A的复共线性增强,有可能呈病态甚至奇异。若采用经典最小二乘方法求解,即使较小的观测误差也会导致解的严重失真甚至错误。解决该问题以得到稳定延拓解的一个途径是对法方程作正则化处理。本文主要讨论标准Tikhonov正则化、岭估计和广义岭估计。不同正则化方法依据不同的正则化准则,正则化参数有所不同。Tikhonov正则化、岭估计只有一个正则化参数α,广义岭估计则是基于多个参数αi(i=1,2,…,N)的正则化方法。正则化参数起到平衡观测误差引起的估值误差和正则化造成的估值偏差的作用。选择最优的正则化参数可使得两项误差之和达到最小。α太小无法有效抑制数据观测误差,太大则使正则化解过于平滑,因此正则化方法的关键在于如何选择合适的正则化参数α。
3.1 Tikhonov正则化
Tikhonov正则化采用如下最小化准则[15]

Tikhonov正则化解为

式中,I为单位阵;α>0为正则化参数。Tikhonov正则化的关键是选择合理的正则化参数α,本文采用广义交叉检验(GCV)确定正则化参数。选取正则化参数的准则为满足下述最小化条件[16]

式中,算子tr表示求矩阵的迹;Qα=A(ATPA+αI)-1ATP。正则化参数的确定采用搜索法,计算步骤如下:
(1)首先在α取较大的区间内(如[1×10-9,10])按式(12)计算F(α)的值,为加快搜索速度α以10倍的量级递增直至上限值,找出F(α)最小值对应的α0;
3.2 岭估计
岭估计的正则化解为[17-18]

式中,α>0为岭参数(正则化参数)。式(13)与Tikhonov正则化解(式11)是相同的,不同之处在于选择正则化参数所依据的准则。岭估计以使正则化解的平均均方误差(MSE)最小作为确定正则化参数的准则。
对式(8)的法方程系数阵作特征值分解

式中,V为法方程系数阵的特征向量组成的正交矩阵,Λ为对角阵,其元素为特征值λ1≥λ2…≥λN>0。式(13)可写为

正则化解的平均均方误差(MSE)定义为平均均方误差矩阵(MSEM)的迹,写成以特征值表示的谱分解式如下[17-18]

式中,zi为列向量Z=VTx^α的第i个元素值。将上式对参数α求偏导数得到
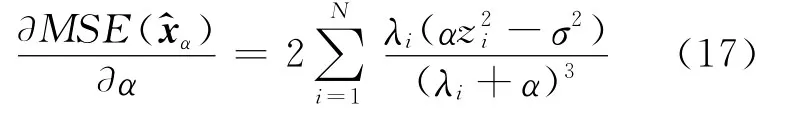
令上式为零,得到关于参数α的方程

满足此方程的α即为能使平均均方误差达到最小的最优正则化参数,可通过迭代计算得到α。由于式(18)是非线性方程,无法直接求解,应采用数值方法求解。具体迭代计算步骤如下:
(1)选取x^α的迭代初始值。用最小二乘法求得的验后单位权方差[KGσ*5]⌒2代替σ2。
(3)若F(c)>0,直接跳到步骤(4);否则,令c=c×s,s>1,重复步骤(2)。
(4)利用二分法求得方程(18)的在区间[0,c]上的根α。
(5)利用步骤(4)中得到的参数α求得正则化解xα。
3.3 广义岭估计
与岭估计相同,广义岭估计也以正则化解的平均均方误差达到最小作为选择最优正则化参数的标准,不同的是广义岭估计需要确定多个正则化参数αi(i=1,2,…,N),而Tikhonov正则化和岭估计只需确定单个正则化参数。由式(13)、式(14)可得广义岭估计的正则化解为[13,17]

式中,Μ是以αi(i=1,2,…,N)为对角线元素的对角阵。正则化解的平均均方误差为

式(20)对参数αi各自求偏导数
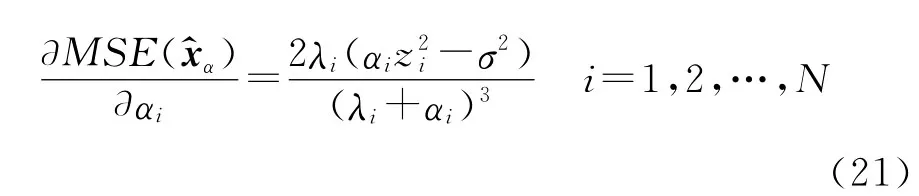
令各自的偏导数为零,解方程即求得使MSE(x^α)达到最小的各正则化参数

最优正则化参数αi和对应的正则化解可迭代计算得到,具体迭代计算步骤如下:
(2)利用σ2和由式(22)计算得到参数αi;
(3)利用步骤(2)中的参数αi由式(19)得到新的正则化解
4 数值计算与分析
为评价上述向下延拓数学模型和正则化方法的数值精度、效率和稳定性,基于EGM2008地球位模型设计模拟试验进行验证。向下延拓采用移去—计算—恢复法(RCR),先由EGM2008位模型的2-2 190阶位系数计算得到飞行高度H处(正高)的重力扰动δg(R+H)观测值,在观测值中加入标准差为1.5mGal的白噪声(模拟观测值统计信息见表1),移去由GOCO01S卫星位模型[19]2-120阶位系数计算的重力扰动得到残余重力扰动δg′(R+H),将δg′(R+H)向下延拓至大地水准面得到延拓值δg′(R);再恢复参考模型值得到大地水准面上的重力扰动延拓值δg(R),延拓过程中采用第二类Helmert凝集法计算地形质量影响。将由EGM2008的2-2190阶位系数计算的大地水准面上的重力扰动作为真实值,比较重力扰动延拓值δg(R)与真实值,可以检验延拓模型和正则化解法的可靠性与稳定性并比较其优劣。为模拟真实航空重力测量条件,选定3个飞行高度,分别是H=2km、3km、4km,数据点格网间隔取2.5′×2.5′,数据点范围为纬线[30°,33°]和经线[107°,110°]围成的区域,共包含5 184个数据点;Poisson积分球冠区半径选取ψ0=1°,为减弱边界效应,计算点范围取纬线[30.5°,32.5°]和经线[107.5°,109.5°]围成的区域,共包含2 304个计算点。分别采用最小二乘法、Tikhonov正则化、岭估计和广义岭估计求解Poisson积分方程(5),将飞行高度处的重力扰动观测值向下调和延拓至大地水准面。采用EGM96位模型计算远区流动点的贡献,最大阶数截断至Nf=360阶,Tikhonov正则化由GCV法确定正则化参数,岭估计和广义岭估计根据迭代算法确定,将观测值作为待求参数的迭代初始值。

表1 重力扰动模拟观测值统计表Tab.1 Statistics of simulated gravity disturbance mGal
表2给出了分别采用最小二乘法和三种正则化方法得到的向下延拓值与真实值的差值统计信息。可以看出,即使对于混入理想化噪声的模拟重力数据,向下延拓解也是不稳定的,延拓高度越大,延拓值与真实值的偏差越大,且在相同的延拓高度上,不同求解方法的延拓结果相差很大。最小二乘解的均方根偏差(RMS)由3.963mGal(H=2km)增大至14.880mGal(H=4km),呈指数上升,表明白噪声随着延拓高度的增加被明显放大,必须引入正则化方法才能获取稳定延拓解。对比三种正则化算法发现:Tikhonov正则化的去噪效果不明显,岭估计能够在一定程度上抑制白噪声,但作用有限,在不同延拓高度处,广义岭估计所得延拓解的精度和稳定性都是最好的,RMS随延拓高度的增大幅度也是最小的,当延拓高度为4km时,广义岭估计解的RMS仅为2.770mGal,仅占岭估计所得延拓值RMS(6.325mGal)的44%,占Tikhonov正则化解RMS(10.627mGal)的26%。
以上数值结果都是在标准差为1.5mGal的白噪声条件下得到的,为检验含较大量级噪声时三种正则化方法的可靠性与精度,分别在重力扰动观测值中加入标准差为2mGal和3mGal的白噪声进行向下延拓计算。表3给出了不同噪声量级时三种方法所得延拓值与真实值的差值统计信息,延拓高度取3km,总体上仍然是广义岭估计表现最优,具有最好的稳健性和抗差性。

表2 重力扰动延拓值与真实值的差值统计Tab.2 Statistics of the differences between continued values and true values mGal

表3 不同噪声量级时重力扰动延拓值与真实值的差值统计Tab.3 Statistics of the differences between continued values and true values mGal
图1是不同正则化解法所得重力扰动延拓值与真实值的差值的空间分布图,延拓高度为4km,白噪声标准差为1.5mGal,从中可以看出,基于广义岭估计的延拓值与真实值的偏差均在±10mGal以内,大部分计算点处的差值不超过±3mGal。相比之下,Tikhonov正则化和岭估计所得重力延拓值与真实值存在较大偏差,特别是Tikhonov正则化的延拓结果严重失真,与真实重力场信号相差甚远,说明延拓过程中噪声放大严重,无法得到可靠的向下延拓解。数值比较结果表明基于多个正则化参数的广义岭估计能够有效抑制测量噪声,实现重力场信号的稳定向下延拓,在可靠性、精度和抗差性等方面都要显著优于基于单个正则化参数的Tikhonov正则化和岭估计。其原因是Tikhonov正则化和岭估计通过在法方程系数阵主对角线元素上加上同一个常数α来改变法方程的病态特性,有可能出现待求参数被高估或被低估的情况,而广义岭估计在MSE(x^α)最小化条件下迭代直至收敛得到每个对角线元素对应的正则化参数αi(i=1,2,…,N),每个正则化解x^αi都对应一个最优的正则化参数αi。

图1 重力扰动延拓值与真实值的差值Fig.1 The difference between continued values and true values
5 结 论
基于EGM2008地球位模型设计模拟试验,分别采用Tikhonov正则化、岭估计和广义岭估计三种正则化方法求解逆Poisson积分问题,将飞行高度处含白噪声的2.5′×2.5′重力扰动向下延拓至大地水准面上,与参考值作外部检验。数值比较结果表明,在延拓精度、稳定性和抗差性等方面,广义岭估计都要显著优于Tikhonov法和岭估计,其原因是广义岭估计需要确定多个最优正则化参数,所得估值具有比普通岭估计估值更小的平均均方误差,而Tikhonov法和岭估计只需确定单个最优正则化参数,有可能出现部分待求参数被高估或被低估的情况。需要指出的是,多个正则化参数的迭代求解带来了广义岭估计解法计算效率相对较低的数值问题,当数据量较大时将全部数据点分块处理可解决这一问题,例如划分成3°×3°的数据块,各数据块之间应保证有一定的重叠区域。
[1] MARTINEC Z.Stability Investigations of a Discrete Downward Continuation Problem for Geoid Determination in the Canadian Rocky Mountains[J].Journal of Geodesy,1996,70(11):805-828.
[4] LI Y C.Airborne Gravimetry for Geoid Determination[D].Calgary:University of Calgary,2000.
[5] KERN M.An Analysis of the Combination and Downward Continuation of Satellite,Airborne and Terrestrial Gravity Data[D].Calgary:University of Calgary,2003.
[6] WANG Xingtao,SHI Pan,ZHU Feizhou.Regularization Methods and Spectral Decomposition for the Downward Continuation of Airborne Gravity Data[J].Acta Geodaetica et Cartographica Sinica,2004,33(1):33-38.(王兴涛,石磐,朱非洲.航空重力测量数据向下延拓的正则化算法及其谱分解[J].测绘学报,2004,33(1):33-38.)
[7] FORSBERG R,KENYON S.Evaluation and Downward Continuation of Airborne Gravity Data—the Greenland Example[C]∥Proc Int Symp Kinematic Systems in Geodesy,Geomatics and Navigation.Banff:[s.n.],1994:531-538.
[8] BÁLHA T,HIRSCH M,KELLER W,et al.Application of a Spherical FFT Approach in Airborne Gravimetry[J].Journal of Geodesy,1996,70(11):663-672.
[9] HWANG C,HSIAO Y,SHIH H,et al.Geodetic and Geophysical Results from a Taiwan Airborne Gravity Survey:Data Reduction and Accuracy Assessment[J].Journal of Geophysical Research,2007,112(B4):1-14.
[10] SHI Pan,WANG Xingtao.The Frequence Domain Analysis for the Determination of Terrestrial Mean Gravity Anomaly Using Airborne Gravimetry[J].Acta Geodaetica et Cartographica Sinica,1995,24(4):301-308.(石磐,王兴涛.空中测量地面平均重力异常的频域分析[J].测绘学报,1995,24(4):301-308.)
[11] SHI Pan,SUN Zhongmiao.The Solution to the Problem of the Spherical Interior Dirichlet and Its Application[J].Acta Geodaetica et Cartographica Sinica,1999,28(3):195-198.(石磐,孙中苗.球内Dirichlet问题解及其应用[J].测绘学报,1999,28(3):195-198.)
[12] NOVÁK P,HECK B.Downward Continuation and Geoid Determination Based on Band-limited Airborne Gravity Data[J].Journal of Geodesy,2002,76(5):269-278.
[13] XU P,RUMMEL R.Generalized Ridge Regression with Applications in Determination of Potential Fields[J].Manuscripta Geodaetica,1994,20:8-20.
[14] HEISKANEN W A,MORITZ H.Physical Geodesy[M].San Francisco:Freeman and Company,1967.
[15] TIKHONOV A N.Solution for Incorrectly Formulated Problems and the Regularization Method[J].Soviet Math Dokl,1963,4:1035-1038.
[16] GOLUB G,HEATH M,WAHBA G.Generalized Crossvalidation as a Method for Choosing a Good Ridge Parameter[J].Technometrics,1979,21(2):215-223.
[17] HOERL A,KENNARD R.Ridge Regression:Biased Estimation for Nonorthogonal Problems[J].Technometrics,1970,12(1):55-67.
[18] XU P.Determination of Surface Gravity Anomalies Using Gradiometric Observables[J].Geophys J Int,1992,110(2):321-332.
[19] PAIL R,GOIGINGER H,SCHUH W D,et al.Combined Satellite Gravity Field Model GOCO01S Derived from GOCE and GRACE[J].Geophysical Research Letters,2010,37(20):1-5.
Solution of Ill-posed Problem in Downward Continuation of Airborne Gravity
JIANG Tao1,2,LI Jiancheng1,2,WANG Zhengtao1,2,ZHANG Shoujian1,2
1.School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China;2.Key Laboratory of Geospace Environment and Geodesy,Ministry of Education,Wuhan University,Wuhan 430079,China
Generalized ridge estimate is suggested for solving the ill-posed problem in downward continuation(DWC)of airborne gravity.Three regularization methods are studied to solve the inverse Poisson problem,which are Tikhonov regularization,ridge estimate and generalized ridge estimate.By conducting a simulated numerical experiment designed based on EGM2008 Earth gravitational model,the2.5′×2.5′gravity disturbances with white noise at the flight levels are downward continued to the Geoid.The accuracy and stability of the DWC methods are tested and compared.The numerical results show that,in terms of continued accuracy,stability and robustness,the generalized ridge estimate based on multiple optimal regularization parameters performs significantly well.
airborne gravity;downward continuation;ill-posed problem;regularization
JIANG Tao(1984—),male,PhD candidate,majors in physical geodesy.
1001-1595(2011)06-0684-06
P223
A
国家自然科学基金(40637034;41074014;40804003;40904003);地球空间环境与大地测量教育部重点实验室测绘基础研究基金(10-02-14)
丛树平)
2010-11-01
2011-04-12
蒋涛(1984—),男,博士生,研究方向为物理大地测量。
E-mail:tjiang@whu.edu.cn

