供应链服务组合招标采购获胜者确定的优化算法研究

马金麟，钱丽娟，刘志强

（1.江苏大学 汽车与交通工程学院，江苏 镇江 212013；2.江苏大学 理学院，江苏 镇江 212013）

供应链服务组合采购的招标问题一直是国内外学者研究的一个重要问题，该类问题主要是解决在供应链环境下如何确定服务采购的获胜者.早期文献对于供应链服务采购的研究大多只是围绕单个服务采购获胜者进行建模求解，而较少涉及多项服务组合采购的情况.但事实上，企业的服务采购是以多产品模式为主的，直到近年来国内外学者才对多产品和多服务的组合采购问题进行了较深入的研究.国外学者ELSEVIER（1984）研究了随机需求下多产品的采购周期问题［1］，ABAD（1989）分析了多产品多市场的采购策略［2］，SONG（2002）等探讨了运输服务组合招标采购的模式［3］，SHEFFI（2004）建立了以运费最小化为目标的服务组合招标采购模型［4］，SAWIK（2007）使用整数目标规划对多产品的生产计划排程和控制问题进行了讨论［5］.国内学者段喆和朱道立（2004）提出了一个多阶段多产品供应量分配的综合模型［6］，关志民等（2005）研究了多产品采购条件下的供应商选择与订购量分配问题研究［7］，陈培友等（2006）建立了多物品最优组合供应模式确定的定量模型［8］，黄河等研究了采购组合投标的均衡策略及多因素采购的获胜者确定问题［9］，杨华龙等探讨了航运服务组合招标采购的算法模型［10］.

上述文献从定性和定量角度都较好地探讨了多物品多服务的采购问题，推动了供应链组合采购研究的向前发展.本文的主要工作则是研究设计供应链服务组合招标采购中获胜者确定的高效算法.根据供应链对多项服务组合采购的需要，建立分散的目标规划模型，借助于混合集合规划的迭代，巧妙地建立模型变量和约束条件之间的数据关系模型，为克服优化目标方向和量纲不同的问题，设计了模糊的欧几里得距离来确定获胜者.求解编码使用NCL语言，优化平台为POEM软件.

1 供应链服务组合招标采购问题的数学描述

1.1 问题提出及解决思路

设供应链中某企业需要采购N种服务，标记为j，j∈ ｛1，2，…，N｝，采购方根据服务的特点和要求面向M个服务提供商进行招标采购，投标者标记为i，i∈ ｛1，2，…，M｝.各投标者能够提供其中一种或几种服务产品，并且在报价、服务质量、企业信誉等方面有较大或略微的差异.假设投标者i的 投 标 组 合 为 ServiceSupplier＿｛i｝， 则 集 合ServiceSupplier＿｛i｝在内容上是全部N 种产品的任意组合，各个ServiceSupplier之间在服务组合的评价属性分别为：priceServiceSupplier＿｛i，j｝、qualityServiceSupplier＿｛i，j｝和reputationService－Supplier＿｛i，j｝.

该问题的解决是以效用最大化为原则择优选择中标企业集合.然而，分别以低成本、高质量和高信誉为目标得到的最优解未必是同一投标者的报价、质量和信誉，因此要经过量纲处理后将所有投标者的属性与最优解price＊、quality＊和reputation＊做欧几里得距离比较，距离最小的投标者将被确定为组合投标的获胜者.

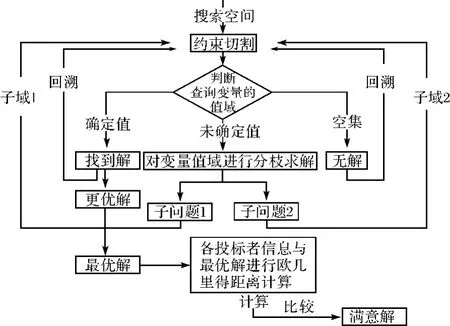
图1 供应链服务组合招标采购的优化思路Fig.1 The optimizing thought of combinatorial bidding purchase in supply chain

1.2 基本假设

针对该问题，做出如下基本假设：

1）采购方的N类服务产品可同时向一个或多个投标者采购，同一个投标者只有一次投标机会，其投标内容要么是其中的一种服务，要么是多种服务产品的组合，对应着服务产品的报价也是一种或多种服务的报价.

2）不重复中标.即同一种服务的投标者中只有一个获胜者，也就是说任意一种服务产品j，不可能出现多个投标者同时中标的情况.

3）采购方的所有服务产品，都要在招投标中得以采购实现.

4）参与投标的企业“要么组合获胜，要么投标失败”，即如果某投标者i中标，其投标的服务组合ServiceSupplier＿｛i，j｝将全部中标；反之，如果投标者的ServiceSupplier＿｛i，j｝中出现某一投标服务j没有被选中，则 ServiceSupplier＿｛i，j｝全体中标失败.

5）采购方可以根据自身情况，限定最小／最大中标者的数量，以控制采购质量.

6）采购方考虑到与供应链合作伙伴的关系，可以指定某以往合作企业为获胜者之一.由于增加新的供应链伙伴可能会带来额外的成本，因此采购方在服务采购计划中有指派某投标者的权力.

7）投标方的服务质量和信誉可以通过专家打分实现定量化.

2 算法设计

2.1 混合集合规划数据模型

在该问题中，price为数值型信息，将quality、reputation信息做量纲处理，使之也成为数值型信息，通过集合的混合规划描述为如下数据模型：

1）输入数据模型

表1 服务产品信息表（OPT＿SERVICE）Tab.1 Information table of service product

表2 投标者信息表（OPT＿SUPPLIER）Tab.2 Information table of service suppliers

表3 投标者与服务组合的匹配表（OPT＿CONSISTENCY）Tab.3 Consistency information between services and suppliers

2）输出数据模型

表4 中标企业信息表（OPT＿ACTIVESUPPLIER）Tab.4 The winning information of winning suppliers

2.2 约束规划算法

在约束规划中，各变量之间的逻辑关系十分重要.所有的采购和投标数据经过上述2.1中的数据模型规划后，从逻辑关系上转变成为集合之间的约束：

1）中标服务组合约束

投标者i的服务投标组合记为ServiceSupplier＿｛i｝，通过布尔值变量（0－1变量）将ServiceSupplier＿｛i｝部分放入到模糊的集合ActiveService中.

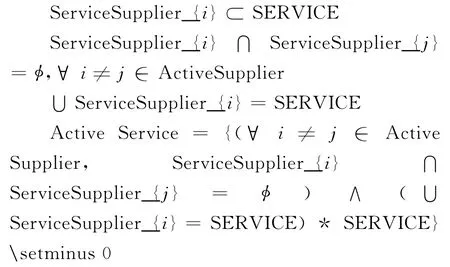
2）中标者约束

3）关联约束

2.3 满意解设计

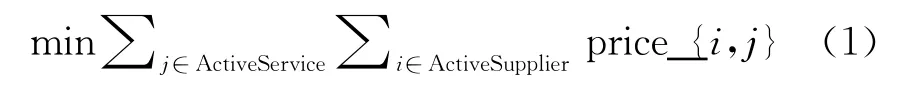
（1）～（3）的分别所得的最优解所对应的最优目标值为：price＊，quality＊，reputation＊.假设某个虚拟的投标者ActiveSupplier＊，其报价组合为price＊，质量组合为quality＊，信誉组合为reputation＊，采用模糊的欧几里得距离求出与虚拟投标者ActiveSupplier＊距离最相近的解ActiveSupplier’.

通过约束条件对解空间切割、枚举、回溯，得到满意解ActiveSupplier’和ActiveService’.

3 算例

模拟一组供应链服务组合招标采购的应用数据，假设某供应链采购商所采购的服务类型为A、B、C、D，采购形式为组合招标采购，参加投标的供应商共有22家，相应的投标组合信息如下表所示，其中质量和信誉的数值信息是通过专家打分法定量化以后得到的数据.

表5 各投标者的投标信息Tab.5 The bidding information of each supplier

采用权重系数来调整采购方对价格、质量、信誉的重视程度，在该算例中，取ω1＝0.4，ω2＝0.35，ω3＝0.25.按照上述算法规则，很快可以得到以下获胜信息：

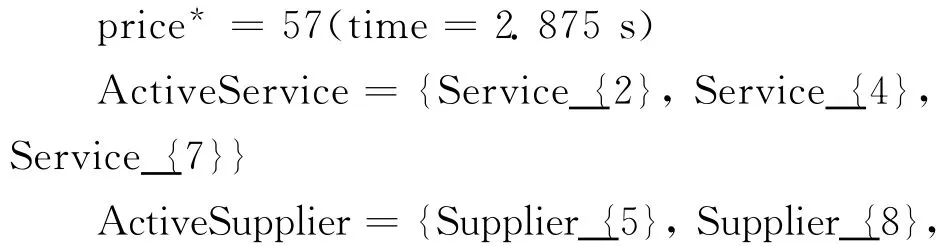
分析该结果，该供应链服务采购的获胜者为：A →S1，B→S5，C→S7，D →S8.算法设计的中间过程中出现的price＊＝57，quality＊＝35和reputation＊＝34，其获胜者的结果不一致，因此假设某一虚拟获胜者组合的服务价格、质量和信誉组合为57，35和34，用实际的各种投标商组合价格、质量和信誉与此虚拟获胜者做欧几里得距离的比较，得到最小值min d＝1.8027755，确定出实际投标者中获胜者组合为S1，S5，S7和S8.采购总价格为59，质量总评分为33，信誉总评分为33，使用PEOM 软件平台总的用时为3.218s（2.875s＋0.156s＋0.078s＋0.109119s）.

4 结论

本文主要从优化算法上对供应链服务组合采购问题进行了研究，通过混合集合规划的数据建模并假设一中间虚拟获胜者组合，求出虚拟组合的最优目标函数值price＊、quality＊和reputation＊，借助price＊、quality＊、reputation＊使用模糊的欧几里得距离计算出实际中的获胜者组合.采购方可以调整权重系数以表示其对价格、质量、信誉等条件的不同重视度.算法使用混合集合表达约束关系，通过模拟算例的实证，证明了该优化算法的实用性和高效性.

［1］Elsevier A.Multi－product stochastic－demand periodic－review inventory and production cycling policies［J］.Inventory in Theory and Practice，1986，3：489－503.

［2］Abad P L.Multi－product multi－market model for co－ordination of marketing and production decisions［J］.International Journal Systems Science，1989，20（11）：2011－2027.

［3］Song J，Rrgan A C.Combinatorial auctions for transportation service procurement：the carrier perspective［J］.Transportation Research Record，2002（1833）：40－46.

［4］Sheffi Y.Combinatorial auctions in the procurement of transportation services［J］.Interfaces，2004，34（4）：245－252.

［5］SAWIK T.A multi－objective customer orders assignment and resource leveling in make－to－order manufacturing［J］.International Transactions in Operational Research，2007，14（6）：491－508.

［6］段 喆，朱道立.多阶段多产品供应量分配的综合模型［J］.系统工程，2004，22（6）：21－24.

［7］关志民，周宝刚，马钦海.多产品采购条件下的供应商选择与订购量分配问题研究［J］.计算机集成制造系统，2005，11（11）：1626－1632.

［8］陈培友，汪定伟.多物品最优组合供应模式确定问题的模型研究［J］.中国管理科学，2006，14（4）：35－39.

［9］黄 河，徐鸿雁，陈 剑.多因素采购组合拍卖获胜者确定问题研究［J］.系统工程理论与实践，2008，28（7）：27－33.

［10］杨华龙，东 方，郑 斌，等.集装箱航运服务多属性组合拍卖模型与算法［J］.交通运输工程学报，2009，9（5）：111－115.