稀土－过渡金属薄膜磁各向异性的理论研究

何一鸣，钱显毅，黄致新

（1.常州工学院 延陵学院，江苏 常州 213002；2.常州工学院 电子信息与电气工程学院，江苏 常州 213002；3.华中师范大学 物理科学与技术学院，武汉 430079）

随着磁记录密度的不断提高，磁记录位的线度也随之不断减小，当记录位里的磁存储能KuV＊与热扰动能kBT可以相比拟的时候（Ku为磁各向异性常数，V＊为记录位的体积，kB为玻耳兹曼常数，T为绝对温度），记录位里原子的热扰动，会破坏粒子之间的交换耦合相互作用［1］，使得记录信号不能持久保存，出现所谓的超顺磁效应［2］.一般认为KuV＊／kBT 的值应为50～70，最低不能小于40［3］.但是，随着记录密度的提高，记录位的体积V＊只会越来越小，为了保持介质的热稳定性并克服超顺磁极限的限制，必须设法提高记录介质磁各向异性常数Ku，或者是采用Ku值较大的材料作为记录介质［4］.虽然Ku值的增大，会使得介质的矫顽力随之增大，磁记录信号难以被写入到记录介质中，但在光磁混合记录方式中，采用的是激光热辅助写入的方式，磁记录信号易于写入到记录介质中.因此，对于光磁混合记录来说，介质的Ku值越大，介质的热稳定性越强，介质的记录密度也可以得到提高.由于稀土 －过渡金属薄膜的磁各向异性能高，其热稳定性强，因此在研究光磁混合记录介质时，必须寻找具有高磁各向异性的介质作为光磁混合记录介质［5］.

自从发现溅射态的稀土 －过渡金属非晶薄膜具有垂直磁各向异性以来，人们对产生这一现象的机制一直在展开相关的实验和理论研究［6］，并提出了相应的理论模型.这些模型主要包括原子对（pair ordering）模型［7］、价键取向（bond－orientation）模型［8］，以及磁偶极模型［9］，但根据这些模型计算的结果与实际的测量值都还有较大的偏差［10］，本文对稀土－过渡金属薄膜的磁各向异性进行了分析和研究.

1 理论分析

虽然磁偶极相互作用能够部分解释稀土—过渡金属垂直磁化膜磁各向异性的来源，但这一解释并不完整［11］.而且由薄膜中的柱状结构（Columanr Structure）（即形状各向异性）而产生的磁各向异性能［12］，或者是由薄膜与基片或底层之间的晶格失配引起的应力所产生的磁各向异性能［13］也太小，不足以解释实验中所观测到的Ku值的大小.因此必然存在着其它的主要因素影响着其Ku值的大小.本文将从溅射成膜过程来出发，计算和分析稀土 －过渡金属薄膜的垂直磁各向异性.

由于在溅射成膜的过程中，从靶上溅射下来的原子在膜面的“敲打”效应（peening effect）［14］，会使得膜面产生压缩应力，结果造成近邻原子壳层的弹性畸变.而且在溅射成膜过程中，薄膜温度也会升高，因此将会产生由热激励引起的滞弹性畸变（anelastic deformation）.在这一过程中，沿膜面方向的新近邻原子壳层将会向中心挤压，而垂直于膜面方向的近邻原子将向外排挤（如图1所示）.在薄膜形成以后，这种近邻原子的排列结果将会被保持下来，形成如图2所示的各向异性的原子排布结构，这种在膜面方向的原子排布较垂直于膜面方向紧密的情形，将产生非球型对称的电场分布，稀土离子的4f电子与非球型对称电场之间的库仑相互作用将有可能导致单轴各向异性的产生.这种只考虑稀土离子的4f电子与非球型对称电场之间的库仑相互作用的模型称为单离子模型.

图1 溅射沉积薄膜过程中原子滞弹性畸变产生结构各向异性的机制示意图Fig.1 Schematic representation of structure anisotropy produced by anelastic deformation during thin films formation by sputtering

图2 薄膜中稀土原子周围最近邻原子的各向异性排列Fig.2 The anisotropy arrangement of nearest neighbor atoms around rare earth atoms

2 理论推导与计算

下面根据单离子模型，采用点电荷近似的方法来进行相关的计算.位于位置→ri处的4f电子与带有电荷数qj在位置→Rj处的最近邻离子之间的库仑相互作用能为：

式中，V（ri）是周围近邻离子所产生的电势，相应地有：

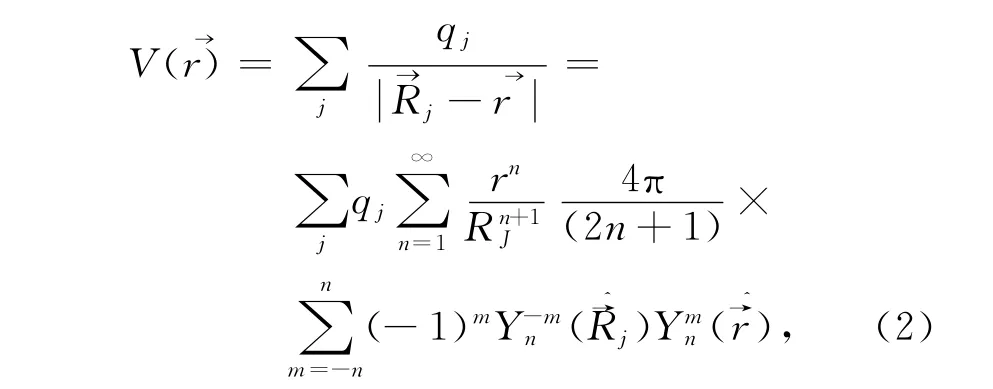
式中，沿极轴方向与单轴各向异性相联系的项为n＝2、m＝0的项，因此有：

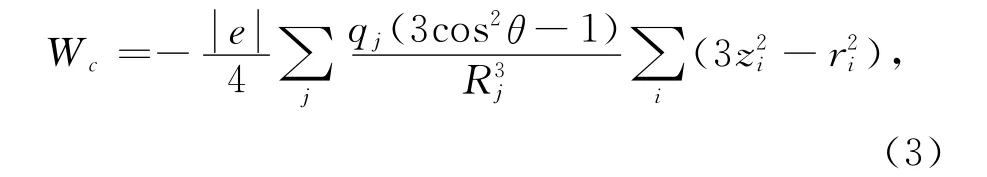
上式中的最后一项通过量子力学的计算［15］后可以用算符表示为：

式中，α是Stevens因子，J为总的角动量量子数，〈r2〉为4f电子波函数的平均分布或轨道半径平方的平均值.于是，（3）式可以变为：

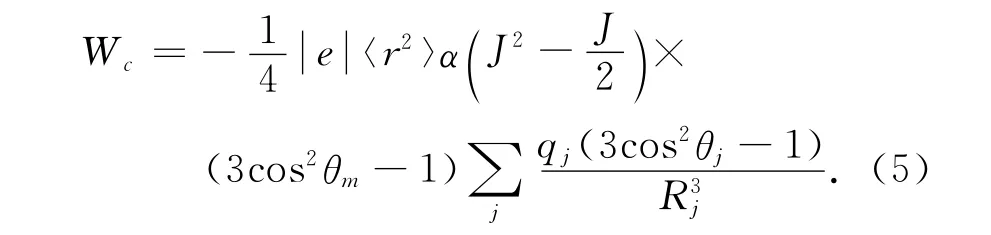
在非晶结构情形，不同近邻原子位置Rj值不相同.因此，（5）式中的求和可以用分布函数积分的形式代替.假设这一分布函数积分用球谐函数形式（1＋δ（3cos2θ－1）／2）dΩ表示，这里参数δ表示膜内局部应变量，则对（5）式积分平均以后可以表示为：

式中，a是最近邻原子的平均距离，Nc是配位数（Coordination Number）.从（6）式可以最后导出各向异性能Ku的表达式为：

式中，n为单位体积内稀土原子的数目.从稀土元素和过渡金属元素原子半径可以估算出组分为R31Co69的非晶薄膜内稀土原子的数目，对于Tb31Co69稀土 －过渡金属非晶薄膜，这一数值若等于3.15×1023cm－3.（7）式中的J、α、〈r2〉的数值可以由文献［15］中查得.q的值可假设为e，对于非晶结构最近邻配位数Nc若为12，Co原子以及稀土离子的Goldshumid半径之和可以视为最近邻原子的平均距离a（约为5×10－9m），稀土 －过渡金属非晶薄膜内局部应变量约为δ＝－0.00024［16］，δ为负值的情况与图1给出的压应力模型相对应.

将文献［15］及文献［16］中所查德的数据代入（7）式，可以计算出薄膜组分为R31Co69的稀土－过渡金属非晶薄膜的垂直磁各向异性能Ku的值如图3所示.从图中可以看出，组分为R31Co69薄膜中稀土元素为Tb时的Ku值最大，接近3.1×106erg／cm3，这是因为Tb是非S态离子，膜内Co原子对的各向异性排列以及原子之间价键取向的各向异性将导致Tb离子的4f电子云也呈现为非球对称分布［17］.这一非球对称分布的离子电荷与溅射沉积薄膜过程中原子滞弹性畸变产生的畸变晶格场之间的静电相互作用构成了TbCo非晶薄膜的垂直磁各向异性的主要部分.因此，无论有无Cr底层，TbCo非晶薄膜都将呈现出很强的垂直磁各向异性.这种具有高Ku值的薄膜材料，可以作为光磁混合记录介质的备选材料［18］.

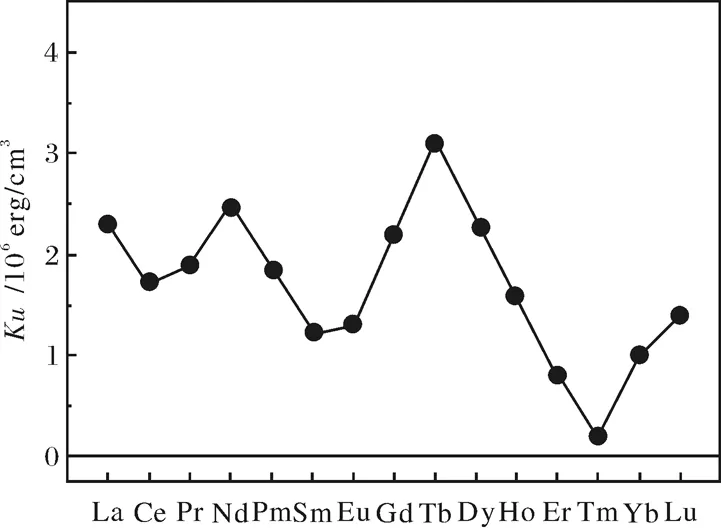
图3 采用单离子模型计算出的稀土 －过渡金属非晶薄膜R31Co69中垂直各向异性能Ku值的大小.Fig.3 The perpendicular anisotropy Ku value of RE－TM amorphous thin films R31Co6calculated with single ion model

3 结论

在溅射成膜的过程中，稀土离子的4f电子与非球型对称电场之间的库仑相互作用将有可能导致单轴各向异性的产生.这种只考虑稀土离子的4f电子与非球型对称电场之间的库仑相互作用的模型称为单离子模型.采用单离子模型的计算结果表明，对于过渡金属非晶非晶垂直磁化膜而言，具有非球对称电荷分布的非S态离子与溅射沉积薄膜过程中产生的畸变晶格场之间的静电相互作用构成了非晶薄膜垂直磁各向异性的主要部分.而且组分为R31Co69薄膜中稀土元素为Tb时的Ku值最大，接近3.1×106erg／cm3.这种具有高Ku值的薄膜材料，可以作为光磁混合记录介质的备选材料.

［1］Grochowski E，Thompson D A.Outlook for maintaining area density growth rate in magnetic recording［J］.IEEE Trans Magn，1994，30（4）：3797－3800.

［2］White R M.Magnetic recording－pushing back the superparamagnetic barrier［J］.Journal of Magnetism and Magnetic Materials，2001，226－230：2042－2045.

［3］Bertram H N，Zhou Hong，Gustafson R.Signal to noise ratio scaling and density limit estimates in longitudinal magnetic recording［J］.IEEE Trans Magn，1998，34（4）：1845－1847.

［4］Charap S H，Lu P L，He Y J.Thermal stability of recorded information at high densities［J］.IEEE Trans Magn 1997，33（1）：978－983

［5］Nagata K，Kawakubo Y，Kato D，et al.Durability of thermally assisted magnetic recording disk［J］.IEEE Trans Magn 2002，38（3）：1332－1334.

［6］Fu Hong，Mansuripor M，Meystre P.Generic source of perpendicular anisotropy in amorphous Rare－earth－transitionmetal films［J］.Physical Review Letters，1991，66（8）：1086－1089.

［7］Mizoguchi T，Cargil G S.Magnetic anisotropy from dipolar interactions in amorphous ferrimgnetic alloys［J］.J Appl Phys，1979，50（5）：3570－3582.

［8］Yan X，Hirsche M，Egami T.Direct observation of annelastic bond－orintational anisotropy in amorphous Tb26Fe62Co12thin films by x－ray diffraction［J］.Physical Review Letters，1991，43（11）：9300－9303.

［9］Hellman F，Gorgy E M.Growth－induced magnetic anisotropy in amorphous Tb－Fe thin films［J］.Physical Review Letters，1992，68（9）：1391－1397.

［10］黄致新，章 平，张玉龙，等.制备工艺参数对TbCo薄膜垂直磁各向异性能的影响［J］.稀有金属材料与工程，2007，36（11）：1947－1950.

［11］Mizoguchi T，Cargil G S.Magnetic anisotropy from dipolar interactions in amorphous ferrimgnetic alloys［J］.J Appl Phys，1979，50（5）：3570－3582.

［12］Cheng S－C N，Kryder M H，Marthur M C A.Stress related anisotropy studies in DC－Magnetron sputtered TbCo and TbFe films［J］.IEEE Trans Magn，1989，25（5）：4018－4020.

［13］Wu C T.In－plane compressibe stress induced by peening effect［J］.Thin Solid Films，1979，64：103－107.

［14］Hutchings M T.Solid State Physics［M］.New York：Academic Press，1964：227－273.

［15］Stevebss K W H.Matrix elements and operator equivalents connected with the magnetic properties of rare earth ions［J］.Proc Phys Soc，1952，A65：209－214.

［16］Waterson R E，Freemann A J.Magnetism［M］.New York：Academic Press，1965：165.

［17］Harris V G，Aylesworth K D，Das B N，et al.Determination of the structural anisotropy in amorphous Tb－Fe films［J］.IEEE Trans Magn，1992，28（5）：2959－2963.

［18］Rauch T，Herget P，Bain J A，et al.Experimental test bed for hybrid recording［J］.Optical Data Storage 2001，43（2）：393－400.