夏至日正午日影测量
2010-12-29 00:00:00郭红锋
中国科技教育 2010年6期

太阳照射到地球上的物体产生了投影。太阳的运动和影子的变化。是日复一日、年复一年的重复现象,我们太习以为常以至于都视而不见了。然而我们的祖先曾经利用太阳影子的测量得出了非常了不起的科学结果,成语“立竿见影”就说明古代人们对日影有普遍的认识。
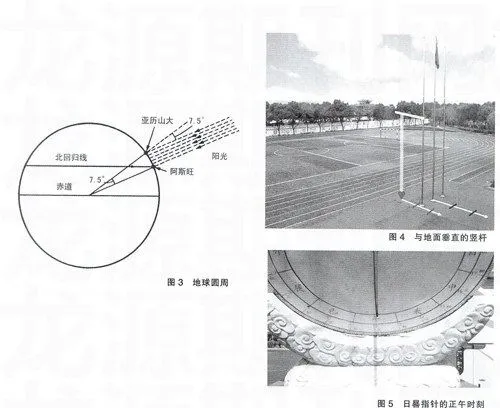
公元前古埃及的科学家埃拉托色尼(图1),通过夏至日太阳影子的测量,计算出地球周长。在古埃及的一个现名为阿斯旺的小镇上,每当夏至日正午。阳光直射,物体是没有影子的。那里有一口深水井,每当夏至日正午,阳光就会直接射入井中(图2-1)。这个有趣的现象引起了很多人的注意并来到这里参观游览。但埃拉托色尼并不是把这一现象仅仅当作当地的一景,而是意识到这一现象里的蕴含的科学信息和自然规律。于是他就记录了阳光直接射入井中的日期和时间,后来又在埃及的另一个城市亚历山大,在同一天的同一时间(当地夏至日正午),测量了当地物体的影子,发现在亚历山大城的夏至日正午。物体是有影子的。按照埃拉托色尼的计算,太阳光线在亚历山大城偏离垂直方向大约7.5°角(图2-2)。
假设地球是球状,那么它的圆周应该是360。(图3)。如果两座城市成7.5°角,相距就是7.5/360的圆周,埃拉托色尼通过查阅大地测量资料,得知两地距离是当时5000希腊里。因此地球周长应该是25万希腊里。换算为现代的公制,埃拉托色尼测算的地球圆周长约为39360千米,与今天通过航迹测算结果(赤道周长=40075千米),误差仅仅在5%以内。
埃拉托色尼巧妙地将天文学与测地学结合起来,精确地测量出地球周长的数值。这一测量结果出现在2000多年前,的确是了不起的,是载入史册的重大成果。
今天。我们已经从地理课本中知道:地球自转轨道和公转轨道之间23.5°的倾角导致一年内太阳直射地球的点在南北回归线之间往复一次。以北半球为例:一年中当太阳直射北回归线时,正值北半球的夏至节气,正午太阳高度角为全年最大值;当太阳直射南回归线时,正值北半球的冬至节气,此时的太阳高度角为一年之中的最小值。这些数据我们可能都倒背如流,但是头脑里的印象却并不深。
我们今天仍然可以参考2000年前埃拉托色尼的测量方法。获得地球参数的第一手资料,以加深我们对书本知识的理解和对自然的感悟。下面就是我们建议全国各tGZF5pHTHBisC1Cen3Wyq/TBkGf5huoZFV0I5keHMUU=地的同学们。在6月22日(夏至日)共同参加的一次测量活动。为使测量得到满意结果。建议同学们提前几天做好各项准备,并反复演练各个操作步骤。
1 活动时间
6月22日正午。
2 活动内容
测量当地太阳影长。
3 活动方法
(1)立竿
在空旷的平地上找一个竖直立在地面上的标志物(可以是一根竿子,也可以是窗户楞、栏杆、旗杆、单杠等固定物)。
(2)垂线
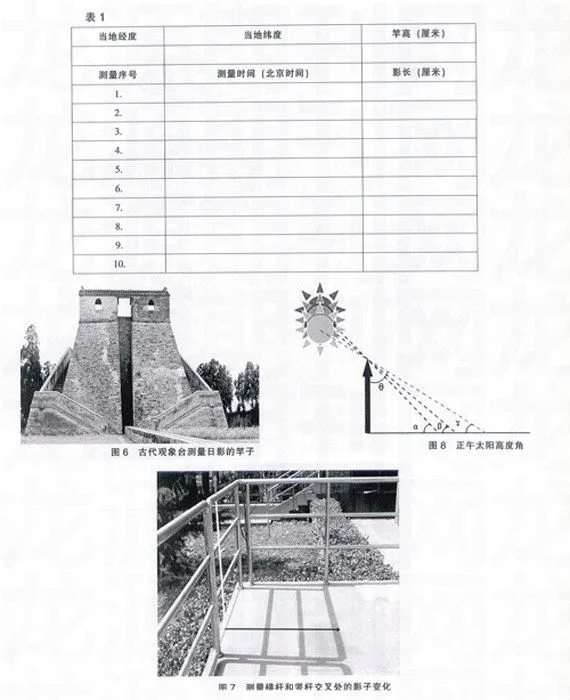
如果是竖直的竿子,本身就与地面垂直,不必再做垂线。如果是栏杆、单杠等横杆。可以用粗线吊重物使之垂直于大地(图4)。
(3)确定当地正午
有日晷的同学可以看日晷指针的正午时刻(图5)。没有日晷的同学要提前几天测量当地的正午时刻,方法是:测量一天中竿子的影长,并记录对应的时刻,找到最短的影长和对应的时刻,就是当日的正午时刻。也可以根据当地的经度和北京时间规定的经度差计算当地的正午时刻(这个工作应该在测量前几天完成)。
(4)测量和记录
用卷尺测量竿子的高度以及投射在地面上的影子长度。从正午时刻前半小时左右开始,每隔10分钟测量一次,直到影长开始逐渐减小,到最小值,然后增大。建议记录如表1。
(5)测量注意事项
由于竿子顶端有虚影。所以竿子顶端在地上的影子末端位置并不容易测准。参考古代观象台测量日影的竿子并不是一根细竿而是最高处平坦的“墙”(图6),所以我们也可以利用栏杆、单杠等平坦的物体,垂吊重物代替竿子,此时测量横杆和竖杆交叉处的影子变化要容易些(图7)。
(6)计算正午太阳高度角
运用构造相似三角形的原理,如图8,求出正午太阳高度角(α)的正切值(tangent),从而计算出该角度大小。查看一下,你的测量结果与当地的纬度有什么关系吗?
(7)验证数据是否精确
运用公式:
太阳高度角=90°-|所在纬度一23°5°|
确定自己所得到的结果是否准确。
公式原理:由于夏至日的正午时刻太阳直射北回归线(北纬23.5°),如图3,可知太阳光线与竿所成夹角θ为当地所在纬度与北回归线纬度的差。又由三角形内角关系得到:太阳高度角+90°+θ=180°,从而整理得到上面的公式。
(8)数据提交
测量数据可以在线提交到http://www.china.hou.org/earth,请注意填写个人信

