基于无标度网络的考虑远程感染的SIRS模型

马爱娜,黄樟灿

(武汉理工大学理学院数学系,湖北武汉 430070）

基于无标度网络的考虑远程感染的SIRS模型

马爱娜,黄樟灿

(武汉理工大学理学院数学系,湖北武汉 430070）

考虑感染节点以一定的概率感染其邻居节点和非邻居节点的实际情况,提出一种具有远程感染机制的SIRS传染病模型,通过计算机仿真得到了最终感染密度随感染率变化而变化的情况。研究发现,具有远程感染的疾病,在传播过程中随着远程感染率的增大感染密度会变大。在现实中可以制定措施控制非相邻节点的接触,降低远程感染率的影响,实现对疾病的有效控制;同时可以通过提高未染病个体的免疫力以及加强染病个体的治疗来更好地控制疾病的发生和传播。该结果对于基于无标度网络的传播控制具有重要启示:在网络信息(疾病、谣言）的传播过程中,只要充分利用感染节点的信息及在传播过程中随机选择少量节点进行主动感染,即可显著增加网络中感染节点的比例,提高网络的传播效率。

无标度网络;SIRS模型;远程感染;最终感染密度

疾病传播作为复杂网络中传播动力学的一个分支近年来引起了众多学者的关注,目前研究最为广泛的疾病传播模型是SI[1]、SIS[2]和SIR[3,4]模型。但以上模型均假设人与人之间存在接触,通过模型的求解最终得到疾病变为地方病的传播率阈值;如果疾病变为地方病,通过计算得到最终感染节点密度的一个精确值。

复杂网络上的传播动力学模型设定:只有存在联系的节点(熟人）之间才能相互传染疾病,而没有联系的节点(陌生人）之间不会传染。陈关荣等提出了一种复杂网络上具有感染媒介的SIS模型,对于无标度网络考虑感染媒介更具有实际意义,并给出了相应的控制策略[4];李光正等[5]提出了一类SIRS模型,证实了复杂网络上疾病传播的决定因素是网络的拓扑结构;在此基础上,夏承遗等[6]提出了带有直接免疫的SIRS类传染病模型,进一步说明了直接免疫和免疫丧失速率对传播临界值的重要影响。然而,以上模型是基于熟人之间疾病才可以传播。现实中熟人(有边连接）和陌生人(无边连接）的划分并不确定,即网络的拓扑结构并非一经确定不再改变。针对这一情况,本文提出了一种考虑陌生人可能与感染节点发生接触的SIRS模型,并将其应用于无标度网络上。

1 无标度网络上考虑远程感染的SIRS模型

在无标度网络[7,8]上的疾病传播过程中,由于具有幂率分布的节点度不具有特征标度,因此必须考虑节点度的非均匀性,用 Sk(t）、Ik(t）、Rk(t）分别表示 t时刻节点度为k的易感类(健康）、感染类和免疫类节点的相对密度,则有:

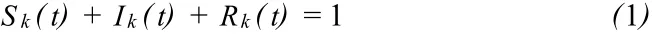
而整个网络感染病节点的比例为:

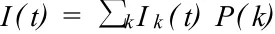
设ө(t）表示t时刻一条随机边与染病节点相连的概率,且满足ө(t）=∑kk P(k）Ik/＜k＞。在无标度网络中易感节点(S）被其相邻的感染节点(I）感染的概率(感染率）为β,而被非相邻的感染类节点感染的概率(远程感染率）为β1;通过治疗作用,感染类节点变为易感节点的概率为δ2,转变为免疫类节点(R）的概率为γ;而易感节点通过直接免疫作用转变为免疫类节点的概率为α,同时免疫类节点转变成易感类节点的概率为δ1。各类节点之间转变过程见图1。

图1 具有远程感染的SIRS模型的传播过程

根据平均场理论及图1中各类节点间的转变过程,可以得到无标度网络上考虑远程感染的SIRS模型:

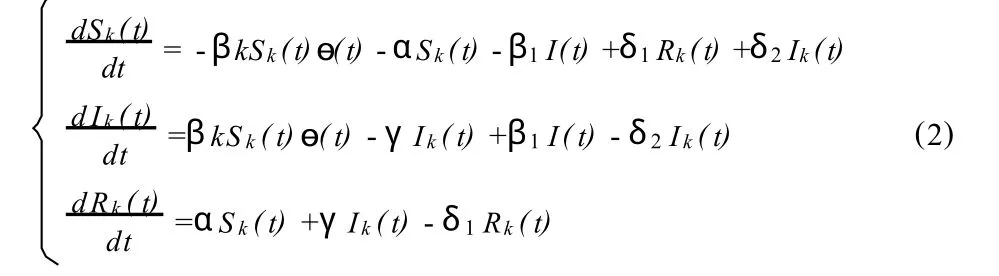
2 模型的仿真值及其分析

通过分析式(2）,很难通过微分方程的方法求得其解析解,运用工具Matlab7.0求最终感染密度的仿真解,并画出最终感染密度随感染率β的变化图,以下仿真的无标度网络[7]的节点数均取N=3 000(节点数改变时可以用同样的方法进行仿真）。

2.1 远程感染率β1对感染密度的影响

取γ=0.02、δ1=0.1、δ2=0.02、α=0.1而β1分别为0、0.1、0.4时,最终感染密度随感染率β的增大而增大(图2）。当感染率较小时,远程感染对最终感染密度的影响非常明显,尤其当感染率为0时,最终感染密度会随着远程感染率的增大而明显增大;而当感染率较大时(如β≥0.3）,远程感染率对最终感染密度的影响不明显。因此为了更好地控制疾病的传播,应考虑远程感染的影响,并加强对非邻居节点的控制。

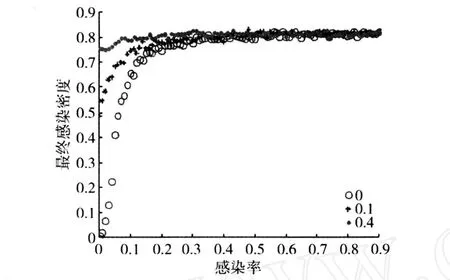
图2 远程感染率的影响

2.2 直接免疫率α对感染密度的影响

取γ=0.02、δ1=0.1、δ2=0.02、β1=0.1而直接免疫率α分别为0、0.1、0.4时,最终感染密度随感染率β的变化如图3所示:在疾病感染率小于0.3时,直接免疫率对最终感染密度有着重大影响,最终感染密度随着直接免疫率的增大而变小,说明在疾病的传播强度(传染率）较小时,可以通过直接免疫的方法加强对疾病传播的控制。

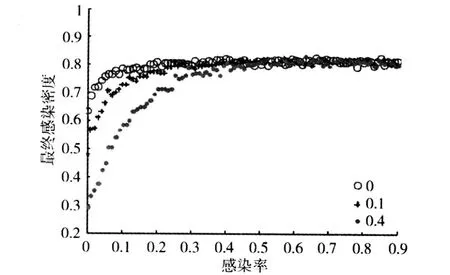
图3 直接免疫率的影响

2.3 治疗作用对感染密度的影响

取δ1=0.1、δ2=0.02、β1=0.1、α=0而γ分别为 0、0.01、0.1时,最终感染密度随感染率的变化如图4:当感染率不变时,随着γ的增大感染密度越来越小。因此可以通过治疗作用来增大参数γ的值,从而有效控制疾病的传播。

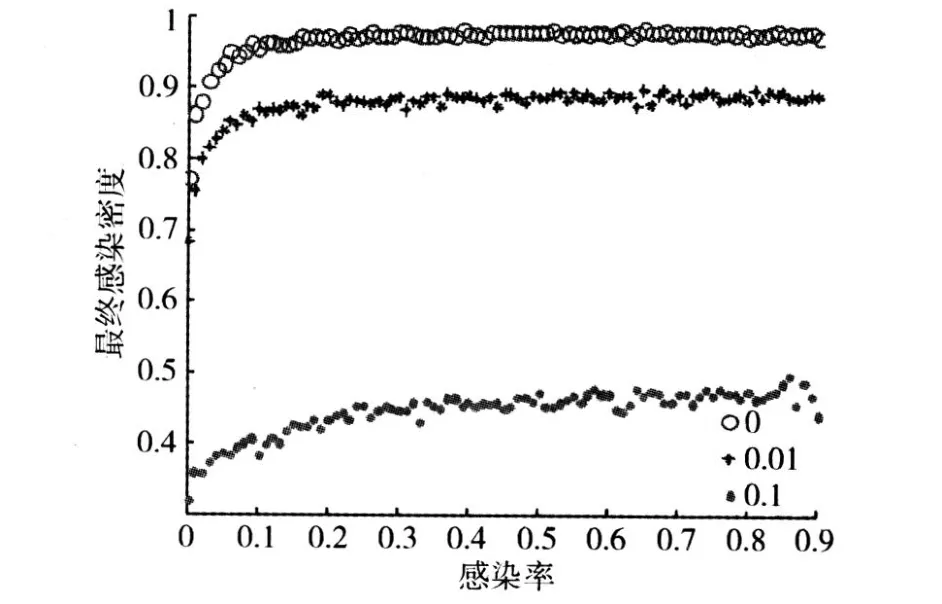
图4 γ的影响

取参数γ=0.1、δ2=0.02、α=0而δ1分别为0、0.01、0.1时,最终感染密度随感染率的变化如图5:随着δ1的增大感染密度越来越小。可见,通过有效的治疗作用可以控制疾病的传播和发展。

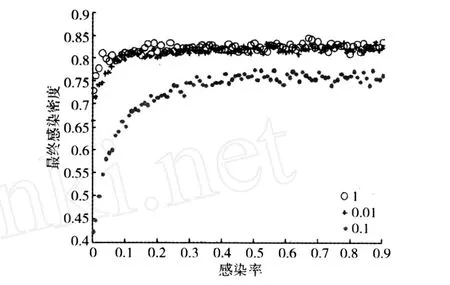
图5 δ1的影响

3 结论

本文提出了一种考虑感染节点以一定的概率感染其邻居节点及其非邻居节点的SIRS模型,并将其应用在无标度网络上。实验表明,感染密度随着感染率的增大逐渐增大,并且可以预测一种疾病是否会变为地方病;如果变为地方病,可以发现其影响的严重程度,从而有效控制疾病的大肆传播。本文基于无标度网络上具有远程感染机制的SIRS模型的仿真结果对于现实生活具有重要意义,对于考虑远程感染机制的其他模型及在其它网络上的应用有待于进一步研究。

[1] PEI Y Z,L IU S Y,L IC G.et,al.The dynamics of an impulsive delay SImodelwith variable coefficients[J].Applied Mathematical Modelling,2009,33:2766-2776.

[2] SH I H J,DUAN Z S,CHEN G R.An SISmodel w ith infective medium on comp lex networks[J].Physica A,2008,387:2133-2144.

[3] MANOJIT R.HOLT R D.Effects of p redation on host-pathogen dynamics in SIR models[J].Theoretical Population Biology,2008,73:319-331.

[4] L IX Z,L IW S,M IN IG.Stability and bifurcation of an SIR epidemicmodel with nonlinear incidence and treatment[J].Applied M athematics and Computation,2009,210:141-150.

[5] 李光正,史定华.复杂网络上SIRS类疾病传播行为分析[J].自然科学进展,2006,16(4）:508-511.

[6] 夏承遗,刘忠信,陈增强,等.复杂网络上带有直接免疫的SIRS类传染模型研究[J].控制与决策,2007,23(4）:468-472.

[7] 汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].北京:清华大学出版社,2006.

[8] BOCCALETTIA S,LA TORAB V,MORENOD Y,et al.Complex neworks:Structure and dynamics[J].Physics Reports, 2006,424:175.

2009-08-17;

2009-12-30

马爱娜(1984-）,女,硕士研究生,主要研究方向为系统控制及优化。E-mail:xiaomaaing@163.com