基于地图方里网的全球剖分系统

耿晓晖,程承旗,宋树华,李大鹏

(北京大学遥感与地理信息系统研究所,北京 100871）

基于地图方里网的全球剖分系统

耿晓晖,程承旗,宋树华,李大鹏

(北京大学遥感与地理信息系统研究所,北京 100871）

针对现有剖分模型的不足,提出了一种基于地图方里网的全球剖分系统,有效避免了传统经纬度格网模型在高纬度地区的形状退化和正多面体格网模型的面片形状不规则问题。制定了相应的编码,实现了面片编码与传统地理坐标之间的转换和邻接关系的计算,最后对方里网在地球椭球面上的变形规律进行了研究。研究结果表明:基于地图方里网的剖分系统不仅具有科学的数据组织形式,而且面片单元的变形面积小、变形规律稳定。

全球剖分系统;方里网;高斯克吕格投影;Mo rton码

0 引言

随着空间技术和对地观测技术的飞速发展,人们能够更加方便地获取有关地球及其各种资源、环境和社会现象的多分辨率的、海量的、实时的对地观测数据[1]。面对海量空间数据管理问题,传统的空间信息表达、组织、管理和发布方式已不能满足全球数据管理的要求。因此,需要构建一个新的基于全球的、多尺度的、融合了空间索引机制的、无缝的、开放的层次性空间数据管理框架[2-4]。基于各种格网模型的全球剖分系统成为解决这一问题的新思路,现有的剖分系统主要有经纬度格网剖分系统、正多面体格网剖分系统和自适应格网剖分系统[1]。邓雪清等采用经纬度格网模型剖分的方法[5,6],该方法计算简单,保持与原有地理数据格式的兼容性,但在高纬度地区存在明显的形状退化。赵学胜等采用正多面体格网模型剖分的方法[7,8],该方法避免了高纬度地区的形状退化,但面片多为三角形、菱形和六边形,不符合计算机的表达习惯,往往运算复杂。自适应格网模型的面片形状取决于采样点的分布,缺乏几何规则性。

将方里网作为剖分模型,能够有效地避免上述模型存在的缺点:方里网不但在平面内形状统一、量测方便,而且根据高斯投影的变形规律,纬度越大并行越小,所以不存在两极退化;同时高斯投影属于等角投影,即相互垂直的两条直线投影之后夹角仍为90°,保持了面片角点的正方形特性。本文以方里网为基础,构建一种基于地图方里网的全球剖分系统。

1 方里网作为剖分模型的难点和解决方法

方里网是一种建立在某种地图投影基础上的格网系统,将制图区域按平面坐标或按经纬度划分为格网,以格网为单位描述或表达其中的属性分类、统计分级以及变化参数,即在二维上表达动态时空变化的规律[9]。方里网作为全球剖分模型存在的难点主要是跨带问题。如图1所示,在平面坐标系上投影带之间存在缝隙,缝隙间的格网属于外部面片,如果利用高斯公式直接反算至地球椭球面,会造成邻带方里网之间的重叠、压盖,如果通过边界经线切割后直接去除,会破坏投影带在平面上的连续性,增加统一编码的难度。

图1 方里网面片的跨带Fig.1 Kilo-grids step across the projection zone

本文采用的方法是:首先在平面内对所有的面片进行统一编码,然后判断面片与投影带的关系,并以属性的方式进行标识。方里网面片分为3种:1）内部面片。面片的4个角点在投影带内部,可以通过高斯反解公式直接计算至球面[9]。2）外部面片。面片4个角点在投影带外部,不做至球面的计算,只存储一个编码,保证平面计算的连续性,所以也可以认为是虚拟面片。3）边界面片。面片的部分角点在投影带内,需要投影带的切割,只将在投影带内的部分反算至球面。最后将面片的边界属性存储至面片编码。在计算过程中首先进行边界属性判断,根据面片的边界属性分别做不同处理,保证在平面内编码的统一,同时避免了将外部的方里网反算至地球球面造成方里网重叠。

2 基于方里网的球面剖分系统

2.1 剖分系统的建立和编码

基于上述解决方案,笔者提出构建基于地图方里网的全球剖分系统的总体思路:以1 km×1 km的方里网为基础,以四叉树的形式向上综合、向下等分,编码的方式采用Mo rton码。

Morton码是一种线性的四叉树编码方式,其基本思想是:不需记录中间结点和使用指针,仅记录叶结点,并用地址码表示叶结点的位置,编码规则如图2,编码与行列数间的转换表示为[10]:

式中:i,j表示面片行列,m(i,j）表示面片的Morton码:int(）为向下取整运算,mod为求余函数。

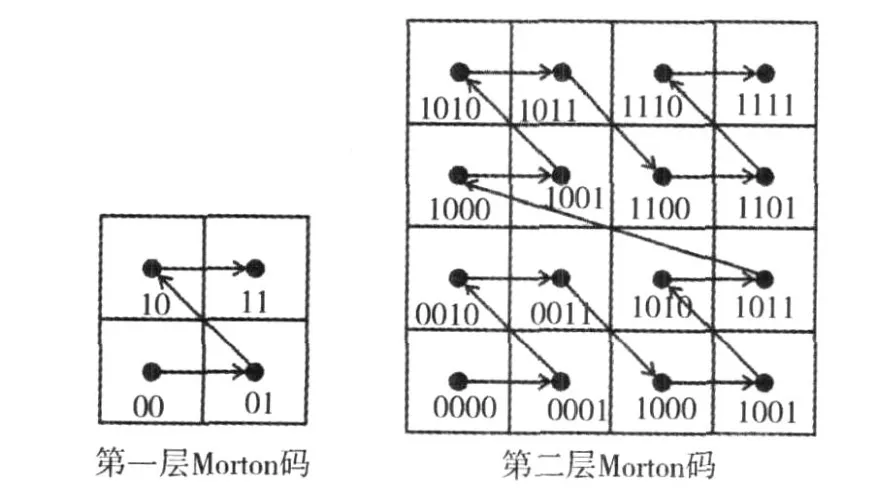
图2 Morton码的编码规则Fig.2 Coding rules of Morton

剖分流程如下:1）投影带扩展:经过6°分带后,投影带中央经线的长度为2×10 002 km,在赤道的宽度为2×334 km,为了能够以四叉树的形式组织面片,投影带的长宽必须是2nkm,所以首先将投影带的长度扩展为2×10 240 km,宽度为2×512 km。2）初级面片划分:首先通过投影坐标轴将扩展后的投影带划分为4个象限,然后将每个象限等分为20行,这样整个区域被划分为4×20个512 km×512 km的面片,其编码方式为:象限号(quadrant）、行号(row）。3）次级面片划分:以初级面片为基础以四叉树的形式向下等分,得到4个大小为256 km× 256 km的面片,作为第二级面片,编码方式采用Morton码。依此类推可以得到大小为128 km× 128 km、64 km×64 km、…的第二级、第三级、…、第n级面片(图3）。4）边界属性判断:通过高斯反解公式[9]计算面片的4个角点坐标经度值,如果全部在两条边界经线的经度范围之间,为内部面片,全部超出该范围为外部面片,其余为边界面片。

图3 基于方里网剖分系统的面片划分规则和编码Fig.3 Division and coding rules of the subdivision system based on Kilo-grids

方里网剖分面片编码包括5项(图4）:1）面片级别(level）:定义最高的面片为20级(第20级为米级）,用5位二进制数表示。2）投影带号(zone）:全球共60带,用6位二进制数表示。3）初级面片编码(prim ary）:包括象限号(quadrant）、行号(row）。其中,象限数为4,可用2位二进制数表示,行数最大值为20,则可用5位二进制数表示,所以初级面片总共可以用7位二进制数表示。4）基于四叉树的Morton码:由1个变长码组成,面片级别每增大1级, Morton增加2位,总共可以用2×level位表示。5）边界属性(border）:共有内部、外部和边界3种面片属性,可以由2位二进制数表示。

图4 基于方里网剖分面片编码Fig.4 The code of a Kilo-grid tile

2.2 面片编码与经纬度之间的转换

方里网面片的编码不仅可以标识面片,而且包含足够的空间定位信息,可以方便地与经纬度之间进行换算,具体换算关系如下。

通过编码计算经面片中心点的经纬度坐标:

(1）初级面片编码(primary）分为象限号(quadrant）、行号(row）,通过象限号确定高斯坐标的正负号,计算初级面片的左下角点高斯坐标(X0, Y0）,X0=512×row,Y0=0;

(2）用公式(2）将Morton码转换为面片的行列号(i,j）;

(3）计算面片中心点的高斯坐标(X,Y）;

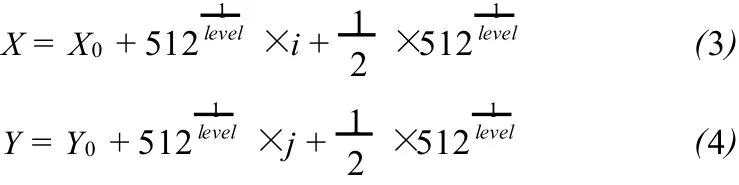
(4）运用高斯坐标反算公式计算该点的经纬度坐标(B,L）;

(5）算法结束。

通过经纬度求面片编码:

(1）确定投影带号:zone=L/6;

(2）通过高斯正解公式计算该点的高斯坐标(X, Y）;确定初级面片:通过X、Y的正负符号确定象限数,计算行数,row=X/512,得到初级面片编码;

(3）将初级面片四等分划分为4个面片,求出相应的编码和4个角点的坐标,记下包含(X,Y）的面片编码,记录其Mo rton码;

(4）对第 3步做level次循环即得到完整的Morton码;

(5）判断面片与边界的关系,确定面片的边界属性(border）;

(6）算法结束。

2.3 基于面片编码的邻接算法

以投影带中的第一象限为例,算法如下:

(1）通过Morton码计算面片在投影带中的行列数(i,j）;

(2）计算相邻面片的行列数:左面片(i-1,j）,右面片(i+1,j）,上面片(i,j+1）,下面片(i,j-1）;

(3）通过公式(1）计算邻接面片编码:左面片m (i-1,j）,右面片m(i+1,j）,上面片m(i,j+1）,下面片m(i,j-1）;

(4）判断面片边界属性,组合各编码分项,得到完整编码;

(5）算法结束。

3 方里网面片的变形研究

方里网在地球椭球面上的面积变形可以通过高斯克吕格投影的长度变形公式进行计算,公式推导过程为:高斯克吕格投影后的长度变形公式取前两项,即:

其中:B为纬度,l为相对经差,η=e′cosB,e′为第二偏心率[9]。

将长度变形公式平方之后得到面积变形公式,取前两项为:

以上是椭球面至平面的面积变形,取倒数得到平面至椭球面的面积变形:

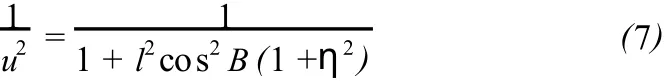
椭球面上的微分梯形计算公式为:

式中:e为第一偏心率,a为地球椭球的长半轴[9]。

这样方里网在地球椭球面上的面积变形可以通过积分计算:

其中:(B0,l0）、(B1,l1）为方里网投影到地球球面上的地理坐标范围。

定义方里网面积变形系数Ф:

以1 km×1 km、2 km×2 km面片为例,参数采用2000国家大地坐标系的地球椭球参数,在相应位置的方里网面片的变形系数如表1、表2。

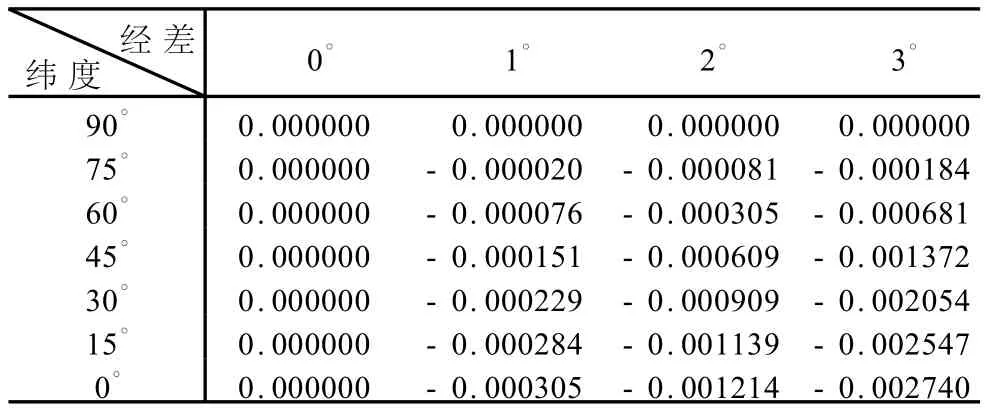
表1 1 km×1 km面片投影后的面积变形Table 1 Area distortion of the 1 km×1 km Kilo-grid tiles due to map projection

表2 2 km×2 km面片投影后的面积变形Table 2 Area distortion of the 2 km×2 km Kilo-grid tiles due tomap projection

从表1、表2得出如下结论:1）方里网面积变形系数全部小于等于0,即方里网投影到椭球面上之后面积变小;2）变形系数较小,以2 km×2 km的面片为例,最大变形数量级为10-3;3）对于同一大小的方里网面片,面片变形随着相对中央经线的经差增加而增大,随着纬度的增加而减小;4）方里网最大的变形面片在纬度为0°、经差为3°处,所以该系统不适合低纬度地区的地理信息表达。

4 结语

本文通过方里网剖分模型,构建了一种全新的剖分系统,以四叉树为基础,制定了相应的编码,研究了面片的变形。结论如下:1）编码高效。采用变长Morton码,只对叶结点编码,隐含了叶结点的位置和大小,节省了存储空间;编码中含有面片的内外属性,为下一步的空间计算奠定了基础。2）具有较好的量测性。方里网具有天然的距离和面积量测属性,符合人们在平面的空间认知习惯,适用于大、中比例尺空间数据的表达。3）具有等角性质。高斯投影属于等角投影,即角度变形为0,方里网投影之后,4个角仍然为直角,最大限度地保证了面片的正方形结构。4）变形稳定。存在面积和长度变形,符合高斯投影的变形规律。

方里网面片在高纬度地区变形较小,与传统的经纬度模型优势互补,因此构建两者结合的混合模型,并研究两个系统之间编码的相互转换方法,将是下一步研究的重点。

[1] 冉令辉.全球空间信息剖分编码模型研究[D].北京大学,2008.

[2] Dutton G.Improving locational specificity of map data——A multiresolution,metadata-driven app roach and notation[J].Int.J.Geographical Information Systems,1996,10(3）:253-268.

[3] GOODCH ILD M.Discrete global grids for digital earth[A].International Conference on Discrete Global Grids[C].California: Santa Barbara,2000.

[4] KIM ERL ING A,SAHR J.Comparing geometrical properties of global grids[J].Cartography and Geographic Information Science,1999,l26(4）:271-288.

[5] 邓雪清.栅格型空间数据服务体系结构与算法研究[D].中国人民解放军信息工程大学,2003.

[6] 杜莹.全球多分辨率虚拟地形环境的金字塔模型研究[D].中国人民解放军信息工程大学,2006.

[7] 赵学胜.全球离散格网的空间数字建模[M].北京:测绘出版社,2007.

[8] 张永生.地球空间信息球面离散网格——理论、算法及应用[M].北京:科学出版社,2007.

[9] 王家耀.地图学原理与方法[M].北京:科学出版社,2007.

[10] 龚雪晶.基于Morton码的图像分裂合并算法研究[J].计算机工程与设计,2007,28(22）:5440-5443.

Global Subdivision Systems Based on Map Kilo-Grids

GENG Xiao-hui,CHENG Cheng-qi,SONG Shu-hua,L IDa-peng
(Institute of Remote Sensing and GIS,Peking University,Beijing 100871,China）

Kilo-grid is the grid fo rmed by the evenly spaced parallels of the p rojection coordinate axes.Re-p rojecting the kilogrids onto the earth ellip soid results in the subdivision of the earth ellipsoid,and this avoids the shape degeneration of the traditional geographic grid model in the high-latitudes and the irregularity p roblem of the meshes of the polyhedral-based discrete grid models effectively.Based on the quad-tree structure between the gridsof different levels,the acco rding mesh code is established on the basisof Mo rton Code and the transfo rmation between traditional geographic coordinates and the mesh codes and the calculation method of the adjacency relationship of meshes are imp lemented.In the end,related research is done on the distortion rules of Kilo-gridson the earth ellipsoidal surface.The results indicate that though there existsarea disto rtion w hen p rojecting themeshes to the ellipsoidal surface,the distortion is minor and follow s strict rules,w hich makes the Kilo-grid Model suitable as a basic Global Subdivision Model.

Global Subdivision System;Kilo-grids;Gause-Kruger p rojection;Morton code

P208

A

1672-0504(2010）02-0015-04

2009-10-27;

2009-12-22

国家重点基础研究发展规划(973）项目(61399）

耿晓晖(1979-）,男,硕士研究生,主要从事地理信息系统研究与工程应用。E-mail:gengxiaohui2007@126.com