图的无圈染色
魏立鹏,何文杰,黄大江,吴文文
(河北工业大学理学院应用数学研究所,天津 300130)
图的无圈染色
魏立鹏,何文杰,黄大江,吴文文
(河北工业大学理学院应用数学研究所,天津 300130)
我们证明最大度Δ≥5的图的无圈色数至多是,这个结果比目前公认的最小上界要小。同时得出两个新的结论:对任意Δ=5的图G,有a(G)≤8;对任意Δ=6的图 G,有a(G)≤12。
无圈染色;无圈色数;最大度
1 引言
设G=(V(G),E(G))是一个连通的简单图, V(G)和E(G)分别表示G的顶点集和边集。记Δ(G),δ(G)分别是图G的最大顶点度和最小顶点度。对于任何一点u∈V(G),用N(u)表示u的邻居的集合。图G的一个正常k-点染色是用k种颜色对图G的点集进行染色使得任意相邻的点染不同的颜色。图G中的一个圈叫2-色圈如果它在正常着色中只用了二种颜色。一个图G的无圈染色满足以下两点:(i)G是一个正常染色;(ii)G不包含2-色圈(亦即染任意两种颜色的点的导出子图是一个森林)。记图G的无圈色数a(G)表示图G无圈染色所需的最少颜色数。无圈染色的概念最早由 Gr¨unbaum提出,并且进一步进行了研究,见文献[3-6,8-11]。关于图G有固定值的最大度问题,A lon等人利用概率的方法证明:当Δ→∞,任何最大度为Δ的图的无圈染色使用至多O(Δ43)种颜色;同时也存在最大度为Δ的图的无圈染色需要种颜色。进一步,他们使用婪算法证明了任何一个最大度为Δ的图使用Δ2+1种颜色。这个结果后来被改进为a(G)≤Δ(Δ-1)+2。1979,Burnstein证明了对于任何Δ(G)=4的图a(G)≤5。近年来,Skulrattanakulchai证明了对于任何Δ(G)=3的图a(G)≤4。对于任何一个最大度为Δ的图,Fertin和Raspaud改进了A lon等人的结果,并证明了它的无圈色数至多是a(G)本文进一步改进了 Fertin和 Raspaud关于最大度的图的无圈染色结果,证明了任何最大度为Δ≥5的图a(G)在下面的讨论中,如果没有特殊证明,我们都假定Δ≥5。
定理1.1 对于任意Δ≥5的图G,有a(G)
为了证明这个定理,首先,先证明下面的引理。
引理1.1 对于任意δ(G)<Δ(G)(Δ≥5)的图G,有a(G)
2 Proof of Lemma 1.1
在证明定理之前,我们先介绍一些定义如下。
定义1 图G的一个部分染色是V(G)的子集颜色的分配满足染任意两种颜色的点集诱导出的子图是无圈的。
定义2 对于图G的一个部分染色c,c(u)记作u所染的颜色。Nc(u)是N(u)中所有染色点的集合,SC(nc(u))={c(ui)|ui∈Nc(u)}是N c(u)中所使用的颜色的集合,nc(u)=|Nc(u)|。显然|SC(nc(u))|≤nc(u)。
定义3 对于图G的一个部分染色c,对于ux∈Nc(u),并且ux≠u0。如果对应于图G的一个部分染色c,不存在c(u0)=c(ux),那么u0∈Nc(u)叫做u的一个单染色邻居,u称为单染色点;否则是u的一个复染色邻居,u称为复染色点。
定义4 对于图G的一个部分染色c,设Nc′(u)表示u所有复染色邻居的集合,有nc′(u)=|Nc′(u)|。显然,nc′(u)≤nc(u)。
为了使读者有一个更直观的了解;我们考虑一个最大度Δ≥5的部分染色图G,u是图G中一个末染色的点,ui(i=0,1,2,3,4)代表u所染色的邻居,ci(i=0,1,2)代表u的邻居所染的颜色。相关无圈染色定义的解释在图1中给出了说明:u是一个复染色点,u0和u1是u的单染色邻居,u2、u3和u4称为u的复染色邻居。Nc(u)={u0,u1, u2,u3,u4},nc(u)=5,SC(nc(u))={c0,c1,c2}, N′c(u)={v2,v3,v4},n′c(u)=3。显然,n′c(u)≤nc(u),|SC(nc(u))|≤nc(u)。

图1 一个复染色点u
应用贪婪算法证明引理1.1,首先把图G中的点接线性序排列:使得v1,v2,…,vn满足:
运满满平台上的520万卡车司机,按年龄分为60后、70后、80后、90后四个群体。从年龄分布来看,卡车司机中既有快到法定退休年龄的“老司机”,也有刚刚步入社会的“小鲜肉”。

接下来,按上面的顶点序逐一贪婪的染图G中的点,依次为点vi分配一个最小颜色标记,要求分配给vi一种还没有被它邻居使用的颜色,并且在每一步染色过程中,需要保证图G是无圈部分染色。于是,得到下面三个有用的观察。
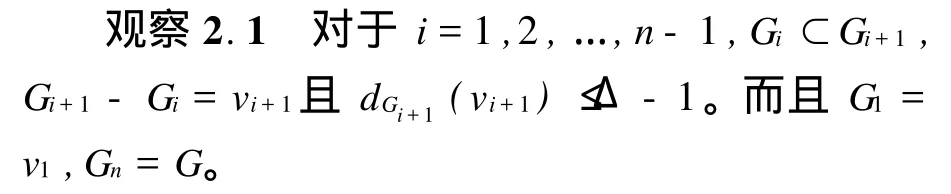
观察2.2 让Gi是一个无圈染色图,u=vi+1是图G中一个未染色的点。为了给u正常染色,它应该避免的颜色数目至多是|SC(nc(u))|≤
很容易检验上面两个观察是正确的。
观察2.3 让Gi是一个无圈染色图,u=vi+1是图G中一个未染色的点。如果Nc′(u)={u1, u2,…,unc′(u)},给u染色为了避免出现2-色圈,它应该避免的颜色数目至多是
证明 对于每一个ui(1≤i≤nc′(u)),它的邻居的颜色数目是|SC(nc(ui))|。在染u的时候,它需要避免出现 2-色圈的颜色数目至多是
根据上面这些观察,下面给出引理1.1的证明。
证明 设G是一个无圈染色图。在图G中至多使用种颜色,它是足够染图G中的点u=vi+1,使得图Gi+1保持无圈染色。
情况1nc′(u)=0.在这种情况下,u是一个单染色点,给u染色的时候不会出现2-色圈,因此它只需要避免在Nc(u)中出现的至多Δ-1种颜色,而
情况2 2≤nc′(u)≤Δ-2。


(B2)在Nc(u)中有一种颜色只出现二次。不失一般性,可以假定在Nc(u)中u1和u2有相同的颜色。首先重染其中的一个,比如u1,根据上面的点序,我们认为u1在u2的后面。为了完成这个任务,考虑u1的两个染色的邻居有相同的颜色,比如u11和u12。
(a)在Gi{u1}中,如果|SC(nc(u11))|=|SC (nc(u12))|≤Δ-2,可以重新染u1,使得u1和u2使用彼此不同的颜色。在重染u1时,它可以使用的 颜 色 数 目 至 少 是」种颜色为了回避可能出现的2-色圈,Δ-2种颜色为了保持正常染色,最后一种颜色是u1的最初颜色。在这个在重染过程之后,我们得到了图Gi的一个新无圈染色,并且满足nc′(u)≤Δ-2(根据G的新部分染色,u2一定变成了u的一个单染色邻居)。因此,根据上面的情况2,为了无圈的染u,它需要至多种颜色。
(b)在Gi{u1}中,如果u11和u12至少有一个(比如u11)满足|SC(nc(u11))|=Δ-1,我们重染u11。在重染u11时,它需要避兔至多(Δ-1)+(Δ种颜色,而后得到Giu1的一个新染色,使得|SC(nc(u1))|=Δ-1。接下来重新染u1使得u1和u2有彼此不相同的颜色(根据情况2.2)。这些重染操作之后,余下的工作按照上面的情况2处理。综合上面的讨论,我们完成了引理1.1的证明。
3 Proof of Theorem 1.1
在下文中,我们假定图G是Δ-正则的。设图G*是由图G删除一个点x(非割点)得到的。图G*是有n-1个点的图,并且有δ(G*)<Δ, NG(x)={x1,x2,…,xΔ}。不失一般性,NG*(xΔ)∩{V(G*)NG(x)}≠φ(根据G*的连通性)。我们把图G*中的点按一个线性序排列:使得v1, v2,…,vn-1满足:

在这种情况下,图G*染色和上面证明图G的δ<Δ染色部分一样。首先用彼此不同的颜色ci(i=1,2,…,Δ-1)染vi。只需要贪婪的染vi(i=Δ,Δ+1,…,n-1)用至多种颜色。最后,对于G*=G{x},我们得到一个无圈染色φ,它需要至多种颜色。注意vi(i=1,2,…Δ-1)的颜色ci在整个染色过程中是不变的。为了证明这一点,我们给出下面的引理。
引理3.1 在上面染色过程中,能够保证vi(i=1,2,…Δ-1)的颜色ci是不变的。
证明 在上面染色过程中,当我们需要重新给某一点y染色时,有两种情况。第一种情况,在引理1.1的证明中,情况2的子情况2.2,情况3中的子情况 3.1和 3.2(B2)(b)使得|SC(nc (y))|=Δ-1。但是vi(i=1,2,…,Δ-1)必须邻接vn,而且在整个图G染色之前,vn没有被染色,因此在G的任何一个部分染色中,有|SC(nc (vi))|≤Δ-2(i=1,2,…,Δ-1)。第二种情况,在引理1.1的证明中,情况 3中的子情况 3.2(B2)(b)中存在两个点(比如u1和u2)具有相同的颜色。但是vi(i=1,2,…,Δ-1)的颜色ci是彼此不同的。因此,u1和u2至少有一个不在vi(i=1,2,…,Δ-1)中,它位于vi(i=1,2,…,Δ-1)的后面。所以我们不选择任何一个vi(i=1,2,…,Δ-1)重染。
下面的两个推论,由定理1.1令Δ(G)=5,6得到,并且改进了文献[8-9]的结果。
推论3.1 对于任意Δ=5的图G,有a(G)≤8。
推论3.2 对于任意Δ=6的图G,有a(G)≤12。
[1] M.O.Albertson,G.G.Chappell,H.A.Kierstead,A. Kündgen,and R.Ramamurthi,Coloring w ith no 2-coloredp4′s.The Electronic Journal of Combinatorics,2004,11 (1).
[2] N.Alon,C.McDiarmid,and B.Reed.Acyclic colorings of graphs.Random Structures and A lgorithm s,1991,2:277 -288.
[3] O.V.Borodin,On acyclic coloring of planar graphs,Discrete Math.25(1979).211-236.
[4] O.V.Borodin,A.V.Kostochka,A.Raspanud and E.Sopena,Acyclic coloring of 1-planar graphs,Discrete Applied Mathematics,114(2001),29-41.
[5] O.V.Borodin,A.V.Kostochka,and D.R.Woodwall,Acyclic coloring of p lanar graphs w ith large girth,J.London Math.Soc.,60(1999),344-352.
[6] M.I.Burnstein,Every 4-valent graph has an acyic 5-coloring(in russian),Sooˇb scˇ.J.Akad.Nauk Grucin.SSR 93 (1979),21-24.
[7] B.Grünbaum,Acyclic colorings of planar graphs,Iarael J. M ath.14(1973),390-408.
[8] Guillaume Fertin,and AndréRaspaud,Acyclic coloring of Graphs of Maximum degreeΔ,in European Conference on Combinatorics Graph Theory,and App lications,pp. (2005),389-396.
[9] Guillaume Fertin and AndréRaspaud,Acyclic coloring of Graphs of Maximum degree five:nine colors are enough, Inform.Process.Lett.105(2008),65-72.
[10] G.Fertin,E.Godard and A.Raspaud,Acyclic and k-distance coloring of the grid,Information Processing Letters. 87(2003),51-58.
[11] S.Skulrattanakulchai,Acyclic colo ring of subcubic graphs, Information Processing Letters.92(2004),161-167.
Acyclic coloring of graphs
WEILi-peng,HEWen-jie,HUANGDa-jiang,WUWen-wen
(A pplied M athematics Institute,Hebei University of Technology,Tianjin300401,China)
Any graph w ith maximum degreeΔ≥5 has acyclic chromatic number at mosta(G)≤」is p roved.This result is less than the best general upper bounda(G)and two new conclvsions are drew as follow s:a(G)≤8,if any graph ofΔ=5;a(G)≤12,if any graph ofΔ=6.
Acyclic colo ring;Acyclic chromatic num ber;M aximmm um degree
O157
:A
1001-9383(2010)04-0004-05
2010-09-21
国家自然科学基金资助项目(10871058)
魏立鹏(1984-),男,内蒙赤峰人,研究生,研究方向:图的染色问题.

