FFT算法的并行化性能分析

王 璐，梁 涛，王文义

（中原工学院，郑州450007）

FFT算法的并行化性能分析

王 璐，梁 涛，王文义

（中原工学院，郑州450007）

以串行FFTW为基准，从程序运行时间、通信开销两方面分析了基于消息传递型（MPI－FFT）和共享内存型（CUFFT）并行FFT实现的性能.实验表明，并行FFT都可以提升计算速度至FFTW的30～80倍，对于中等规模的数据，CUFFT的计算速度略优于MPI－FFT，且其通信开销明显较低，具有较高性价比和较好的应用前景.

并行性能；CUFFT；MPI；FFTW

离散傅里叶变换（DFT）是数字信号处理中最基本、最重要的运算，许多算法，例如卷积、滤波、波谱分析等都可以化为DFT来实现.但是DFT的计算量相当大，1965年Cooley和Tukey提出了快速傅里叶变换算法（FFT），大大提高了DFT的计算速度.此后，有很多研究者不断改进算法.美国麻省理工学院计算机科学实验室超级计算技术组开发的FFTW（Fastest Fourier Transform in the West）是目前世界上公认的运算较快、使用广泛的串行C程序FFT，支持一维和多维的实数及复数DFT［1］.

随着高性能科学计算的要求和嵌入式技术的发展，不仅产生了多种基于DSP或FPGA的并行FFT实现［2］，而且还出现了多种适于不同并行体系结构及编程模型的并行FFT算法［3－5］.文献［6］对FFT并行化思想进行了简要的总结与分析，面向集群设备给出了基于消息传递接口（MPI）的典型并行FFT算法，是目前针对因高性价比而受到用户青睐的集群并行设备实现并行FFT的重要参考.

目前，基于图形硬件（GPU）的通用计算正成为并行领域的研究热点.特别是NVidia公司于2007年推出统一计算设备架构（CUDA）后，极大增强了GPU的通用计算能力，在编程、优化等方面都得到了显著的提升.同时，NVidia公司基于CUDA也推出了面向GPU的并行FFT算法，即CUFFT.肖江等针对矩阵乘法以及CUFFT进行了计算性能测试［7］.但是更详尽的性能分析，以及与其他典型并行体系结构下的并行FFT算法的比较还很少见.

本文以串行FFTW作为基准，对CUFFT、基于集群与MPI的典型并行FFT算法进行了计算能力以及通信开销的详细比较，以期为各种算法的性能特点及适用场合提供更翔实的应用参考.

1 FFT的并行性分析

FFT的基－2并行计算过程如图1所示［5］.节点｛i，0｝（N／2≤i≤N－1）将接受直线边传来的数据与交叉边传来的数据，通过两点FFT蝶形计算方法可求出下一列向量.以此类推，直到第logN列才变为用原始向量进行计算.所以，经过logN步并行计算后，即可计算出一个N点一维FFT.

图1中数据量为8，并行节点数为4.一般地，若数据量为DataSize，并行处理机节点数为TaskNum，则log2DataSize至log2TaskNum列都是单机的串行处理，从log2TaskNum列至0列是并行处理.经过这样的递归计算，最终把结果数据计算出来.在此过程中，并行计算节点之间需要进行数据传递，且在每一个循环阶段，都要进行同步，才可以进行下一步.

图1 FFT并行计算蝶形示意图

在具体实现FFT并行计算过程时，集群设备通常采用消息传递机制，通过普通以太网络或专用Infiniband网络在各计算节点间进行数据传输，因此需要较多的通信开销.而图形设备（显卡）在进行并行计算时，采用共享内存型的计算模式.特别地，CUDA还提供了全局存储器、共享存储器、本地存储器等多种存储器方案，便于性能调节与优化.与消息传递型相比，GPU的通信主要在图形硬件（显卡）的板级，因此通信更可靠且更快速.

2 并行FFT的性能测试及分析

2.1 测试方案

2.1.1 测试环境

单计算机硬件环境为CPU Intel Pentium Dual E2160 1.80GHZ，内存1G；软件环境为 WinXP操作系统；显卡为NVIDIA公司的GeForce 8400GT，支持CUDA技术；集群环境为22个结点，每个结点由2个2.8GHz处理器组成，内存总量为22G，Infiniband专用网络；分别选用了FFTW库与CUFFT库；编译环境为Micorsoft Visul Studio 2005.

由于当数据量为2的幂次方时，FFT的速度最快，本文对4组二维实验数据进行FFT运算，通过对给定同样大小的数组数据进行处理的时间来进行比较.

2.1.2 测试对象

本文对目前比较重要的并行FFT算法进行测试.因此，选择面向集群及MPI实现的典型FFT算法和面向GPU的CUFFT进行比较测试，代表了目前高性能计算领域2种非常活跃而且通用的并行体系结构.为更好地分析并行性能，仍以串行FFTW算法作为测试基准.

（1）FFTW库程序.FFTW是世界上公认的运算较快的FFT，也是使用很广泛的傅立叶变换程序.具体实现如下：

首先载入数组数据，再建立二维FFTW plan进行数据处理.主要程序如下：

in＝ （fftw＿complex＊）fftw＿malloc（sizeof（fftw＿real）＊Nx＊Ny）；

out＝ （fftw＿complex＊）fftw＿malloc（sizeof（fftw＿complex）＊Nx＊Ny）；

给输入和输出的数据申请内存，这里Nx和Ny分别表示数组的行和列的大小，执行plan，完成FFT；

p＝fftw＿plan＿dft＿2d（NNx，NNy，in，out，FFTW＿FORWARD，FFTW＿ESTIMATE）.

这里，FFTW＿ESTIMATE也可换为FFTW＿MEASRUE，FFTW＿ESTIMATE会更快一些.但如果要处理很多同样大小的数据，用FFTW＿MEASRUE会更好一些，因为如果用FFTW＿MEASRUE模式创建一个最优方案后，只要数据大小不变，在下一次启用时会启动之前创建好的plan，这同样是最优方案.

当数据大小为1024＊1024时，FFTW＿MEASRUE和FFTW＿ESTIMATE运行结果如图2所示.

图2 FFTW＿ESTIMATE与FFTW＿MEASRUE运行结果比较

（2）CUFFT.CUFFT是由NVIDIA提供的基于GPU的快速傅里叶变换（FFT）函数库.它采用分治的算法，对数据能够在实数与复数域进行FFT运算.CUFFT提供了以下功能：

可以对实数或复数进行一维或多维的DFT，可以同时处理一批一维DFT；

对二位和三维的傅里叶变换，每个维度长度在［2，16384］中取值.

具体实现如下：

首先，需要将文档中的数据载入GPU内存中，分别对＊idata和＊odata定义并申请存储空间：

cufftReal＊idata；cufftComplex＊odata；

cudaMalloc（（void＊＊）＆idata，sizeof（cufftReal）＊Nx＊Ny）；

cufftMalloc（（void＊ ＊）＆odata，sizeof（cufft－Complex）＊Nx＊Ny）；

定义plan，创建plan：

cufftHandle plan；cufftPlan2d（＆plan，Nx，Ny，CURRT＿R2C）；

完成FFT变换：

cufftExecR2C（plan，idata，odata，CUFFT＿FORWARD）；

当数据大小为1024＊1024时，运行结果如图3所示.

图3 CUFFT运行结果

（3）基于 MPI的并行FFT.MPI（Message Passing Interface）是一个库，FFTW3支持基于MPI的并行编程.具体实现如下：

调用头文件＜fftw＿mpi.h＞，创建计划：

fftw＿mpi＿plan fftw＿mpi＿create＿plan（MPI＿Comm comm，int n，FFTW＿FORWARD，FFTW＿ESTIMATE）；

通过调用函数来进行变换，调用的函数为：void fftw＿mpi（fftw＿mpi＿plan p，int n＿fields，fftw＿complex＊local＿data，fftw＿complex＊work）；

返回时调用函数：void fftw＿mpi＿local＿sizes（fftw＿mpi＿plan p，int＊local＿n，int＊local＿start，int＊local＿n＿after＿transform，int＊local＿start＿after＿transform，int＊total＿local＿size）.

2.2 计算能力比较

测试结果如图4所示.

从图4可以看出，随着数据量的增大（矩阵的行列分别为256，512，1024，2048），并行计算的优势越发明显，MPI－FFT和CUFFT一般比FFTW的运算速度提高30～80倍；MPI和GPU的计算时耗在数据规模较小时相差不大，随着数据规模的增加，GPU计算要稍快.但对于超大规模数据，GPU由于受到硬件容量限制，其并行性能落后于集群设备.由于GPU的造价相对于集群设备MPI更加低廉，普通用户也可以享用多节点并行的技术优势，因此对于中小规模计算具有更高的性价比.但对于超大数据量计算时，一般会选择基于MPI的集群设备.

图43种FFT测试结果

2.3 通信开销

通信开销对比如图5所示.在追求减少计算用时的算法研究的同时，用于计算过程中的数据传递所用的时间，即通信开销，也是必须要重视的因素.在CUDA的GPU运算中，通信的时间主要是发生在从内存拷贝数据到GPU的全局存储器上；基于MPI的并行计算，它的通信时间是在每一级运算完毕后，再把数据分别传递给既定的下一级节点上用的时间.

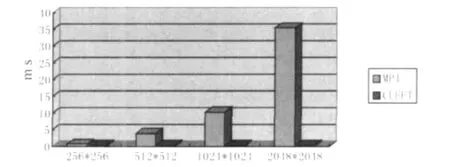
图5 通信开销

本文MPI选取的处理节点数为16，通过图5可以看出（处理节点个数n＝16），MPI的通信开销是比较大的，这也影响了MPI并行计算的效率.而GPU计算的通信时间相对地要少得多，GPU计算在通信开销方面有很大优势.

3 结 语

本文对FFTW、CUFFT以及 MPI－FFT等3种FFT实现方案进行了性能测试.通过计算用时和通信开销两方面的比较可以看出，基于GPU的CUFFT性能在中小数据规模情况下略高于基于MPI的FFT，具有较高的性价比.目前国内CUDA技术的发展研究正逐渐兴盛起来，相比较于大型计算机，CUDA技术使得人们在个人PC机上也能高效地实现大量数据运算，这也将吸引人们投入更多的精力致力于CUDA技术的研究发展.从这个意义上说，CUFFT具有更好的应用前景.

［1］ Matteo Frigo，Steven G Johnson.The Design and Implementation of FFTW3［J］.Proceedings of the IEEE，2005，93（2）：216－231.

［2］ 朱林，王志凌，黄天戍.基于DSP并行系统的FFT算法实现［J］.武汉理工大学学报，2009，31（20）：102－104，120.

［3］ 于泽德.基于SIMD－MC2的并行FFT算法［J］.现代计算机（专业版），2008（10）：57－58.

［4］ 刘文辉.基于SIMD－BF的并行FFT算法［J］.商丘师范学院学报，2003，19（5）：63－63.

［5］ 孙世新，卢光辉，张艳，等.并行算法及其应用［M］.北京：机械工业出版社，2005.

［6］ 张林波，迟学斌，莫则尧，等.并行计算导论［M］.北京：清华大学出版社，2006.

［7］ 肖江，胡柯良，邓元勇.基于CUDA的矩阵乘法和FFT性能测试.［J］计算机工程，2009，35（10）：7－10.

［8］ 张舒，褚艳利，赵开勇，等.GPU高性能运算之CUDA［M］.北京：中国水利水电出版社，2009：10.

Parallel Performance Analysis of FFT Algorithm

WANG Lu，LIANG Tao，WANG Wen－yi
（Zhongyuan University of Technology，Zhengzhou 450007，China）

Performance analysis is the basis of parallel program before applied practically.This paper compares a set of parallel Fast Fourier Transform （FFT）algorithm including FFTW，CUFFT Library and MPI－FFT.Experiments show that parallel program can achieve 30to 80times than serial program （FFTW）in speed.And CUFFT is better than FFT based on MPI in large scale data computing.It has less communication overhead distinctively.

parallel performance analysis；CUFFT；MPI；FFTW

TP391

A

10.3969／j.issn.1671－6906.2010.05.008

1671－6906（2010）05－0030－03

2010－09－29

河南省教育厅自然科学研究项目（2009A520034）

王 璐（1972－），男，辽宁清原人，副教授，博士.