储层渗透率非均质性表征新参数
——渗透率参差系数计算方法及意义
邵先杰
(燕山大学 石油工程系,河北 秦皇岛 066004)
油层非均质性是影响油田产量、最终采收率以及经济效益的重要参数[1-2],如何能够全面、有效、科学、定量地表征储层非均质性是地质学家和石油工程师探索的一个重要问题。储层非均质性是储层沉积、成岩等地质过程综合作用的结果[3-5]。目前能够表征储层非均质性的参数很多,但每一种方法都有其优缺点。在长期的储层研究过程中,经过大量的理论探索与实践,提出了储层表征的新参数——渗透率参差系数,该参数能够比较真实、准确地表征储层的非均质程度。
1 表征参数及方法综述
目前国内外表征储层非均质性的参数很多,常用的有突进系数、渗透率变异系数、级差、变差函数等参数[6-8],另外还有从其它行业引进来的参数,如基尼系数等。
渗透率突进系数表征的是一定井段内渗透率最大值与其平均值的比值,即:
(1)

其值变化范围1~∞,越大越非均质,方法简单明了,但其数值变化范围大,可对比性差。
渗透率级差表征的是一定井段内渗透率最大值与最小值之比,数值变化范围1~∞,同样是数值越小越均质,越大越非均质,这种方法只考虑了最大值与最小值,忽略了中间数值对储层非均质性的影响,不全面,同时也存在数值变化大,可对比性差的问题。
渗透率变异系数是一个数理统计的概念[8],用于度量统计的若干数值相对于其平均值的分散程度。即:

(2)
式中:σ为变异系数;Ki为第i个样品的渗透率值;n为样品数。
其意义反映的是样品偏离整体平均值的程度。数值变化范围0~∞,数值越大越非均质。该参数是一个重要的表征量,国内外常用它来计算数据中的变化特征,其数值变化范围大,只有下限没有上限,可比性差,分类标准不容易确定。
近几年变差函数也常用来描述储层平面的非均质性,变差函数是指区域变化量在某一方向2点处增量方差之半,变差函数的某些特征反映了储层参数的空间变化特征。变差函数描述平面非均质性具有整体性,比较全面,但需要数据多,井点分布要相对均匀,否则代表性差,另外,无法反映纵向非均质性。
基尼系数最早是用来评价国民收入分配的差异程度,它是根据洛伦茨曲线计算得到的[9],后来被地质学家引用到储层渗透率非均质表征方面,也能够比较全面地反映出一组数据的均匀程度。该方法计算过程比较繁琐,并且当数据点比较少的情况下,拟合出的曲线也存在较大的误差。为此,在洛伦茨曲线基础上,提出了表征渗透率非均质性的新参数——渗透率参差系数,该参数计算简便,物理意义更明确。
2 参差系数的计算方法及意义
渗透率参差系数表征的是各样品渗透率值偏离完全均值线的平均值,下面详细介绍其计算方法及意义。
将连续逐点解释的渗透率值或渗透率样品测试值从小到大排成一序列,设有n块样品,并分别从1到n编号。横坐标x轴为样品百分数,即样品的序号与样品总数的百分比。纵坐标y轴为样品渗透率累积百分数,即样品的渗透率累积值与所有样品渗透率总和之比。这样散点图中由n个点组成(图1),其中第m个点的坐标(xm,ym)为:
式中:xm为第m个点的横坐标;ym为第m个点的纵坐标;m为第m个样品。
图中对角线OB为完全均质线,如果样品是完全均质的,即当样品的渗透率值全部相等时,数据点全部落在OB线上[10],在该线上任何一点都满足y=x,即样品百分数等于渗透率百分数。OAB线为完全非均质线,如果全部样品中只有一个样品有渗透率值,其它全部为零时,数据点会落在OAB线上。
渗透率参差系数(Ck)的定义为各样品的渗透率累积百分数偏离“完全均质线”(OB线)的相对值的平均值(图1)。即:
Ck=(Ck1+Ck2+…+Ckm+…+Ckn-1)/(n-1)
Ckm=Δkm/xm;Δkm=xm-ym
(4)
式中:Ck为渗透率参差系数;Ckm为第m个样品点偏
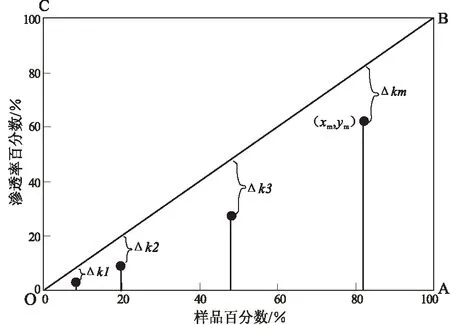
图1 渗透率参差系数计算示意
离完全均质线的相对大小;Δkm为第m个样品点偏离完全均质线的值。
因为Ckn=0,所以只累加到Ckn-1。
Ck是介于0~1之间的小数。Ck=0,表明是均质的,样品点的渗透率值全部相等;Ck=1,表明是完全非均质。
该参数具有以下优点:1)可对比性强,容易划分标准;2)不受样品点的数量限制,样品点多可以计算,少也可以计算;3)计算简便,在电子表格中可以计算,也可以编程计算。
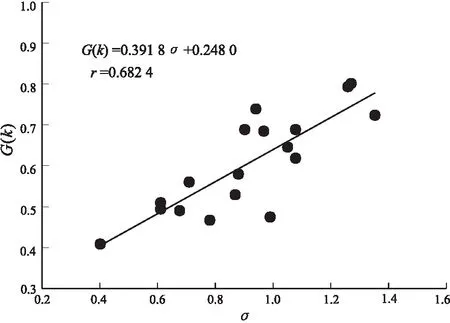
根据对大量实际资料的应用总结,依据渗透率参差系数大小可以把储层的非均质程度划分为4个级别:Ck≤0.4为均质;0.4 利用上述方法,对陈堡油田全区18个层的渗透率数据分别计算了各层的变异系数(σ)、参差系数(Ck)和基尼系数(G(k))。根据计算结果分析,Ck与变异系数σ之间存在很好的线性关系(图2): Ck=0.531 7σ+0.042 4 r=0.849 (5) 式中:r为相关系数。 而基尼系数G(k)与变异系数的相关性见图3,其关系式如下: 表1 江苏陈堡油田层孔隙度、渗透率数据 图2 参差系数(Ck)与变异系数(σ)散点 图3 基尼系数(G(k))与变异系数(σ)散点 G(k)=0.391 8σ+0.248 0 r=0.682 4 (6) 由图2,3及式(5),(6)可见,参差系数与变异系数的相关性好于基尼系数与变异系数的相关性,说明利用参差系数的大小描述储层非均质性的方法是可行的,物理意义也是明确的。 1)渗透率参差系数的首次提出,丰富了油藏非均质性的表征方法。 2)渗透率参差系数可以直观、方便地评价储层的非均质性,可对比性强。同时也可以应用到其它参数的非均质研究方面。 3)在油田的实际应用中取得了良好效果。 参考文献: [1] CHOI K, JACKSON M D, HAMPSON G, et al. Impact of heterogeneity on flow in fluvial-deltaic reservoirs: Implications for the giant ACG field, South Caspian Basin[J]. Society of Petroleum Engineers, 2007:3214-3229. [2] 石磊,匡建超,曾剑毅,等. 川西新场气田沙溪庙组致密碎屑岩储层单井产能评价与预测[J]. 石油实验地质,2009,31(4):338-342. [3] 于翠玲,林承焰. 储层非均质性研究进展[J]. 油气地质与采收率,2007,14(4):15-18. [4] 尹太举,张昌民,李中超,等. 濮城油田沙三中层序格架内储层非均质性研究[J] . 石油学报,2003,24(5):75~83. [5] 陈刚,王正,陈清华. 陈堡油田陈2断块阜宁组阜三段储层非均质性研究[J]. 油气地质与采收率,2009,16(2):20-23 [6] SENOCAK D, PENNELL S P, GIBSON C E, et al. Effective use of heterogeneity measures in the evaluation of a mature CO2flood[J]. SPE73803,2008:1325-1333. [7] ROY B, ANNO P, GURCH M. Imaging oil-sand reservoir heterogeneities using wide-angle prestack seismic inversion[J]. Leading Edge, 2008, 27(9): 1192-1201. [8] KWON S I, SUNG W M, HUH D G, et al. Characterization of reservoir heterogeneity using inverse model equipped with parallel genetic algorithm[J]. Energy Sources, 2007, 29(9): 823-838. [9] 李潮流,周灿灿. 碎屑岩储集层层内非均质性测井定量评价方法[J] . 石油勘探与开发,2008,35(5):595~599. [10] 康晓东,刘德华,蒋明煊,等. 洛伦茨曲线在油藏工程中的应用[J] . 新疆石油地质,2002,23(1):65~67.3 应用实例分析
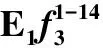

4 结论

