一个传统逻辑的难题
李建华,陈 波
(1.湖南科技大学 法学院,湖南 湘潭 411201;2.北京大学 哲学系,北京 100871)
一个传统逻辑的难题
李建华1,陈 波2
(1.湖南科技大学 法学院,湖南 湘潭 411201;2.北京大学 哲学系,北京 100871)
在传统逻辑中,有一个熟知的难题,即SAP→SEP'→P'ES→P'AS'→S'IP'→S'OP,在这个推理串中,每一步推理都是符合规则的,但总的结果却是违反规则的:在前提中不周延的词项P在结论中却变成周延的!这一结果是由以下三个因素共同造成的:直言命题的主项存在假定,推理规则N:“在前提中不周延的词项在结论中不得周延”,以及关于直言命题中主谓项周延性的四条规定。因此,要解决那个难题,我们至少有三种不同的选择:放弃主项存在假定,修改推理规则N,修改关于周延性的那些规定,而每一种选择都有可接受的后果和不可接受的后果,因而不是一个容易作出的选择。该难题仍然期待一个最终的系统解决方案。
直言命题;直接推理;三段论;主项存在假定;周延性
在传统逻辑中,有下面一个难题,教过逻辑或学过逻辑的人都知道,但长期以来得不到合理的解释,更没有被最终解决:

这个推理由全称肯定命题SAP出发,经过连续的换质、换位推理,最后得到S'OP,其中S'表示S的负概念。这是传统逻辑中由一连串的直接推理构成的一个推理[1]。
直接推理属于演绎推理,而演绎推理是一种必然性推理,其前提的真能够保证结论的真。因此,它允许其结论断定得比前提少,但不允许其结论断定得比前提多;否则,前提的真不能保证结论的真。具体就直接推理而言,它必须遵守一条规则N:“在前提中不周延的词项在结论中不得周延”。这条规则中所谓的“词项”,是指直言命题的主项和谓项,分别用S和P表示。所谓“周延性”(distribution),是指一个直言命题在形式上对S和P的外延范围的断定:如果一个直言命题在形式上断定了一个词项的全部外延,该词项在该命题中就是周延的;否则,它就是不周延的[2](P11-16)。下面四条是关于直言命题中主谓项周延性的规定:
(i)全称命题的主项是周延的;
(ii)特称命题的主项是不周延的;
(iii)肯定命题的谓项是不周延的;
(iv)否定命题的谓项是周延。
于是,我们得到下表:

我们回过头去看开头提到的那个推理:在由之出发的前提SAP中,P是肯定命题的谓项,不周延;而在结论S'OP中,P是否定命题的谓项,周延。这违反了明显合理的规则N。但是,如果仔细考察,这个推理的每一步都是严格按照换质法、换位法的程序和规则来实施的,而最终结果却违反了在推导过程中一直在遵守的规则。这是一个明显的矛盾和悖论!它的存在说明,传统逻辑是不一致的,其推理理论是不安全和不可靠的。这种情况是如何产生的?其原因或根源是什么?如何把它消除掉?显然,以一致性和严格性著称的逻辑学必须对此作出回答,但迄今为止却没有任何人给出了一个前后融贯的、彻底说得通的回答。一般认为,是直言命题的主项存在问题造成了这样的困难。但下面将证明,情况并非必然如此。
可以证明,如果允许在前提中周延的词项在结论中不周延,如果又同时允许对直言命题做连续的换质、换位推理的话,那就得允许在前提中不周延的词项在结论中变得周延,从而违反规则N[3]。兹举三例:
例1:SAP→SIP。这是根据对当方阵中差等关系进行的推理,其中S是全称命题的主项,周延;在结论中是特称命题的主项,不周延。对SAP做连续的换质位推理:-SAP→SEP'↔P'ES↔P'AS',其中每一步都是等值变换。再对SIP做等值变换:SIP↔PIS↔POS'。得到的结果却非常令人惊讶:在前提SAP的等值命题P'AS'中,S'是肯定命题的谓项,不周延;但在结论SIP的等值命题POS'中,S'是否定命题的谓项,周延。这违反了规则N!
例2:SAP→PIS。这是直接推理中的限量换位,在前提中S是全称命题的主项,周延;在结论中,它是肯定命题的谓项,不周延。同样,对SAP做等值变换,得到P'AS',其中S'不周延;再对PIS仅做一步换质推理,得到其等值命题POS'。于是,又得到这样的结果:在前提的等值命题P'AS'中,S'不周延;但在结论的等值命题POS'中,S'周延,再次违反了规则N!
例3:三段论第一格的 AAI式:MAP,SAM,所以,SIP。对大前提MAP做连续的换质、换位推理,得到其等值命题P'AM';对小前提SAM做同样的推理,得到其等值命题M?AS';最后对结论SIP先换位,再换质,得到其等值命题POS'。在小前提的等值命题M'AS'中,S'不周延;而在结论的等值命题POS'中,S'周延,也违反规则N!
这就是说,在传统逻辑中,如果允许有的词项在前提中周延但在结论中周延,那么,就得允许有的词项在前提中不周延却在结论中周延。假如稍加推广的话,在传统逻辑中,如果你允许结论断定得比前提少,那你就要同时允许结论断定得比前提多。这样一来,推理形式不再具有保真性,从而不再是有效的推理形式。这确实非常令人奇怪,但这的确是事实!
在传统逻辑中,允许词项在前提中周延在结论中不周延的推理,最典型的是两类:
(2)差等关系推理:SAP→SIP;SEP→SOP;
(3)限量换位推理:SAP→PIS。
(2)和(3)都涉及所谓的“直言命题的存在含义”,即直言命题假设了其主项不是一个空类,其所指对象是存在的,简称“主项存在”。不过,在现代数理逻辑中,全称命题SAP相当于条件命题,它只断定了主项和谓项的关系,并没有断定主项和谓项本身存在。以“所有的鬼都是青面獠牙的”为例,这个命题只是说:“对于任一x,如果x是鬼,则x是青面獠牙的”。由于无鬼,故该条件命题的前件对个体域中所有x为假,则该条件命题本身对所有x自动为真。这就是说,全称命题不假定其主项所指对象存在,无存在含义。而特称命题SIP却等于说:“存在这样的x,使得x既是S又是P”。即是说,该特称命题至少断定了S存在,亦称“存在命题”。但是,如果全称命题无存在含义,特称命题有存在含义,则从全称命题就推不出相应的特称命题,故SAP→SIP和SEP→SOP这两个推理不再成立。传统逻辑肯定这两个推理成立,它至少要预先假定直言命题的主项所指对象是存在的,简称“主项存在假定”。
不过,由于传统逻辑允许换位推理,直言命题的谓项也可以变成主项,于是“主项存在”也就逻辑地要求谓项存在。同样的道理,由于传统逻辑允许连续的换质位,主项的负概念可以变成谓项,最后再变成主项;谓项的负概念也可以变成主项,例如 SAP→SEP'→P'ES→P'AS'→S'IP',因此,传统逻辑的“主项存在假定”最终演变成:在“所有S是P”这样的直言命题中,不仅要求主项S存在,而且要求谓项P存在,还要求主项的负概念S'、谓项的负概念P'都存在。用现代逻辑的话来说,这等于要求主项S和谓项P都既不是全类也不是空类。以空类为主项的直言命题明显违反“存在假定”,例如“所有长八个脑袋的人都是天才”,按现代逻辑的观点,从这个命题推不出特称命题“有些长八个脑袋的人是天才”,因为后者等于说“有人长八个脑袋,并且他们是天才”,而这是假的。以全类做主项的直言命题也违反“存在假定”,以“所有事物都是发展变化的”为例,其中的主项和谓项都是全类,因为“事物”泛指任一东西,故“事物类”是全类;按照辩证法的观点,万物皆变,无物常住,因此“发展变化的(事物类)”也是一个全类。于是,对该命题换质,得到“所有事物都不是不发展变化的”,其谓项“不发展变化的(事物类)”是一个空类,再换位,得到“所有不发展变化的就不是事物”,再换质,得到“所有不发展变化的都是非事物”,此命题的主、谓项都变成了空类,因而违反了“存在假定”。在传统逻辑中,假设 S、P、S'、P'存在,就是假设它们都既不是全类也不是空类。
应该说,传统逻辑的“存在假定”有其合理性。在日常语言以及我们的常识和直观中,假如把引述、转述他人的话语除外,当我们自己说某句话时,我们一般是在谈论我们自己认为存在的对象。例如,说“所有的鬼都是青面獠牙的”人,一般认为是有鬼的,至少根据那些鬼故事来判定是有鬼的;完全断言无鬼的人不会到处宣扬这个命题,至多是在引述、转述和批判它。传统逻辑就是在“S、P、S'、P'都不是全类和空类”这个假定之下展开的,它的大多数推理模式,例如对当关系推理、换质法、换位法以及连续的换质位,某些三段论推理,都直接或间接地依赖这个假定。例如,只有假定S存在,才能由SAP推出SIP。
但是,传统逻辑的“存在假定”又不尽合理,这是因为:第一,在日常言谈中,我们不仅谈论现实世界的实存对象,我们也谈论神话世界、小说世界以及科幻世界中的对象,谈论有关它们的种种事情。在这样的谈论中,有时候并不假设有主项所指对象存在。例如,“假如一个人的聪明程度与其脑髓的重量确有关联的话,那么,那些脑髓重达4公斤的人肯定是超级天才。”“一个身高10米的人肯定是这个世界上长得最高的人。”在这两句话中,前一句并不假定确实有脑髓重达4公斤的人,后一句也不假定确实有身高10米的人,而只是断定了某种意义关联。再如,说“玩火者必自焚”的人并不假定有玩火者,他说这句话的真正目的是起规劝、警示作用:若谁敢以身试法,必遭惩罚和制裁!第二,自然科学规律常常涉及理想状态,如“所有冷却到绝对零度的物体都是导电体”,这并不意指真的存在冷却到绝对零度的物体;再如,“在摩擦力为零的情况下,静者恒静,动者恒动”,摩擦力为零的状况是很难达到的理想状况,但这些规律却是对现实世界也适用的物理规律。特别重要的是,第三,“存在假定”是关于这个世界的一个实质性假定,涉及到某些事物的存在或非存在,但传统逻辑又试图把它的推理理论发展成为一个纯形式的理论:若给定某个或某些前提,就可以按照一定的程序和规则往下推,而不必时时关注这个世界上究竟发生了什么事情。也就是说,“存在假定”这个实质性假设并不参加实际的推理过程,那么,如何保证这个实质性假定在推理过程中发挥作用呢?如何防止在很长的推理过程中不会发生偏离、违反这个假定的情况呢?这就是存在假定所面临的困境。
现代逻辑学家一般认为,逻辑学应该是关于推理的纯形式结构的理论,与推理中前提和结论的内容无关;保真性是关于形式结构的要求,而不是关于内容的要求。正是这一特质才保证了逻辑理论的普遍可应用性:它适用于人类思维的各个领域,也适用于人类知识的所有学科,适用于千差万别的具体内容。因此,现代逻辑学家通常认为,传统逻辑的存在假定是不合理的,应该抛弃;依赖这个假定的那些推理模式犯有“存在谬误”,即从关于不知其是否存在的事物的断言推出了关于存在事物的断言。
下面的文恩图并不假定直言命题的主项存在[4](P69-145):

图1
它用S和P表示直言命题主项和谓项,用两个相互交叉的圆圈表示S和P之间的关系。包括这两个圆圈在内的整个空间代表论域,用∪表示;这两个圆圈把∪划分成为四个区域:区域 1 为 SP',2 为 SP,3 为 S'P,4 为 S'P'。若某个区域涂有阴影,则表示该区域是空的,没有元素;若某个区域写有加号“+”,则表示该区域有元素,不是空的。例如,A和O命题可用文恩图表示如下:

图2
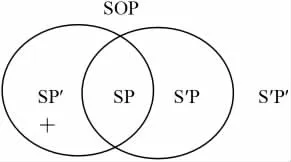
图3
图2只是断定没有任何东西存在于P之外的S部分,在S和P两个圆圈的重叠部分以及位于S之外的P部分没有画任何符号,这意味着:A命题对这些区域是否有元素没有作出任何断言;E命题与此类似。所以说,文恩图没有预设全称命题A和E具有存在含义。而图3在SP'部分画有“+”号,表示这一部分有元素,因而O命题有存在含义;I命题与此类似。
若像文恩图这样不假定直言命题的主项存在,则传统逻辑的推理理论会发生很大的改变,有以下几点:
第一,A和E不再具有上反对关系。即是说,当允许使用空类时,A和E不再是不可同真,而是可以同真。例如,“所有重达1000公斤的超级大胖子都是短命的”,“所有重达1000公斤的超级大胖子都不是短命的”,这两个全称命题在现代逻辑中被翻译为带全称量词的条件句,由于人世间没有重达1000公斤的超级大胖子,该条件句的前件对个体域中所有x是假的,于是该条件句对于所有x就自动地(或空洞地)为真,故A和E这两个句子都是真的。
第二,I和O不再具有下反对关系。即是说,当允许使用空类时,I和O不再是不可同假,而是可以同假。由于特称命题是存在命题,“有些脑髓重达10斤的人特别聪明”(I命题)和“有些脑髓重达10斤的人并不特别聪明”(O命题)都肯定了“有脑髓重达10斤的人”,而这是假的,故这两个命题都是假的。
第三,全称命题和同质的特称命题之间的差等关系不再成立。当允许使用空类作主项的,全称命题就会空洞地为真,而特称命题是存在命题,一律为假,所以从全称命题为真不能推出特称命题一定真,从特称命题为假不能推出全称命题一定假。
第四,限量换位和连续的换质位(或换位质)不再有效。例如,当谓项允许是空类时,经过限量换位后该谓项成为特称命题的主项,即断定了空类不空,而这是假的。例如,“所有的尼斯湖怪兽都是独脚兽”,经限量换位,得到“有的独脚兽是尼斯湖怪兽”,而这个存在命题是假的。在本文开头的那个难题SAP→SEP'→P'ES→P'AS'→S'IP'→S'OP中,包含一步限量换位,即P'AS'→S?IP',因而也不再成立。即是说,若抛弃直言命题的主项存在假定,该难题不再是一个难题,而只是一个谬误推理[5]。
第五,由两个全称前提得出特称结论的9个三段论式不再成立,即第一格的AAI,EAO,第二格的AEO,EAO,第三格的 AAI,EAO,第四格的 AAI,AEO,EAO 都不再有效,因为从无存在含义的前提不能推出有现在含义的结论来。当去掉直言命题的存在含义后,三段论有效的充分必要条件是:(1)中项恰好周延一次;(2)大项和小项在前提和结论中的周延情况应相同;(3)前提和结论中的否定命题数量相同。由此可以导出一条规则:(4)前提和结论中的特称命题数目相同。三段论的有效式缩减为15个。
显然,对于传统逻辑来讲,以上的变动是非常剧烈的,几乎是对它的彻底改造。但是,有不少逻辑学家认为,传统逻辑的推理理论(包括直接推理和三段论),对于处理我们日常语言中的一部分推理来说,仍然是有用的,并且非常方便,有其存在价值。他们力图尽可能地拯救传统逻辑的推理理论,使其前后一贯,并且能够自圆其说,其办法就是把它的存在假定由隐变显,让存在假定参与推理过程。具体就文恩图来说,引入一个新符号“⊕”,表示文恩图中相应的区域不空,有元素存在其中[6]。需要注意的是,“+”表示特称命题本身所固有的存在含义,而“⊕”表示全称命题所隐含的存在假定。这样一来,A命题和E命题可以用文恩图表示如下:

图4
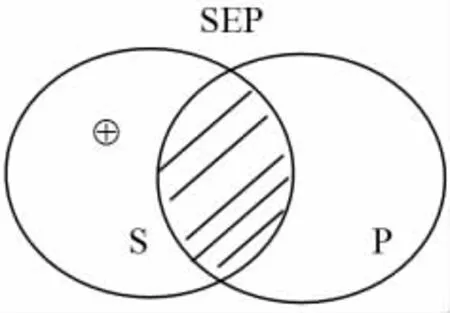
图5
在SAP的图示中,S的左面部分涂上了阴影,表示那是一个空类;因而,如果S类确有对象存在的话,它们一定存在于S和P的重叠部分,故将“⊕”置于该区域。可以用经过如此改进的文恩图,去证明传统逻辑中那些依赖存在假定的推理形式都是有效的[7]。仍然考虑前面分析过的例1、例2和例3:
例1:图4是SAP的经过改进的文恩图,它把SAP的主项存在假设明显化:既然在P之外的S部分没有元素,而S又确实有元素(主项存在),这些元素必定处在S和P交叠区域,故SIP真,SAP→SIP这个推理形式有效。
例2:理由与上例相同。
例3:需要先简短说明如何用经过改进的文恩图去验证一个三段论式是否有效。由于三段论包含S、M和P三个词项,因此需要三个相互交叠的圆圈,如下图所示:

图6
图6把整个空间(论域U)分割为8个区域:1为MS'P',即那些是M但不是S且不是P的元素所占的区域;2为MSP',3 为 MSP,4 为 MS'P,5 为 SM'P',6 为 SPM',7 为 M'S'P,8 为 M'S'P'。
用文恩图验证任一三段论式是否有效,其步骤如下:
第一,画三个相互交叠的圆圈,分别代表三段论的小项S、大项P和中项M;
第二,在图解两个前提时,如果有一个是全称前提,另一个是特称前提,应先图解全称前提,并且要注意把隐含的存在假定明显化,在适当区域画上“⊕”这个符号;在图解特称前提时,要注意表示某部分不空的记号“+”所放的位置,假如不能确定应放在线的哪一边,就把它放在线上[8]。
第三,然后检查该文恩图,看两个前提的图解是否包含了结论的图解;如果包含了结论的图解,该三段论是有效的,否则就是无效的。
再回过头去看例3所谈到的三段论第一格AAI式:MAP,SAM,所以,SIP。举例来说,“所有脑髓量大的人都是特别聪明的人,所有脑髓重达四公斤的人都是脑髓量大的人,所以,有些脑髓重达四公斤的人是特别聪明的人。”我们用M代表“脑髓量大的人”,S代表“脑髓重达四公斤的人”,P代表“特别聪明的人”,则该三段论的正规文恩图如下:
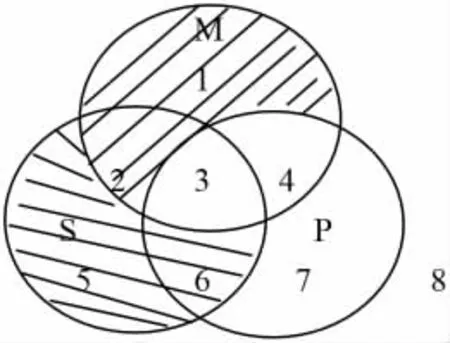
图7
图7只说区域1、2、5、6没有元素,没有说区域3有元素,所以在前提MAP、SAM都真时,不能断定结论SIP为真,AAI式无效。不过,若使直言命题主项存在假定明显化,则可用改进的文恩图来图示该三段论式:

图8
根据存在假定,大前提的主项M存在,既然M不在区域1和2,则它必定处在区域3和4的交界处;由于小前提的主项S存在,故S必定在区域3,而区域3是S和P的重叠处,故SIP真,第一格三段论式AAI有效。
不过,把直言命题的主项存在假定明显化,让它参与到实际的推理过程中,这一做法等于把“存在假定”变成了“存在断言”,于是,
SAP等于一个合取命题:“有S,并且所有S都是P”;
SEP等于一个合取命题:“有S,并且所有S都是P”;
SIP等于一个存在命题:“存在个体x,使得x既是S又是P”;
SOP等于一个存在命题:“存在个体x,使得x是S但不是 P”。
在对A、E、I、O作如此解释之后,它们之间的对当关系会发生很大变化:A与O、E与I之间不再有矛盾关系,而有反对关系;I与O之间相互独立,没有真假关系;A与I、E与O之间仍然有差等关系[4](P80-89)。当然,一些直接推理形式的有效性也会发生改变。更重要的是,按照这样的处理,在本文开头提到的那个难题中,每一步推理都会是有效的,但最终结果却是无效的:在前提中不周延的谓项P在结论中变成了周延的,从而违反规则N!而那个难题是下面三个因素共同作用的结果:直言命题的主项存在假定,推理规则N:“在前提中不周延的词项在结论中不得周延”,以及关于直言命题的主谓项周延性的四条规定[9]。
因此,要解决传统逻辑中的那个难题,我们至少有三种选择:第一,抛弃直言命题的主项存在假定,于是,在本文开头提到的那个长推理串中,限量换位P'AS'→S'IP'这一步不再成立,故由SAP就推不出S'OP,该难题不再成为难题。但由此付出的代价是:对传统逻辑的推理理论做剧烈修改,许多在常识和直观中有效且管用的推理形式不再成立。第二,把推理规则N强化成N':“词项在前提和结论中的周延情况应相同:若一词项在前提中周延,则应在结论中周延;若它在前提中不周延,则应在结论中不周延。”这样一来,差等关系推理SAP→SIP和SEP→SOP,以及限量换位推理SAP→PIS都不再有效,这等于否定了直言命题的主项存在假定,所带来的后果也与第一种选择相同,只是还需要加上一条:N'在直观上非常不合理:它不允许在前提中周延的词项在结论中不周延,这等于要求:至少在词项的周延性上,演绎推理的结论不应该断定得比前提少或者弱,而应该与前提断定得一样多或一样强,这几乎会毁掉演绎推理的必要性!第三,修改关于直言命题中主谓项周延性的那些规定。人们通常对A、E、I中主谓项的周延情况不持异议,问题在于O中的谓项是否总是周延的:例如,当S和P为相互交叉的类和完全不相交的类时,由SOP可以得出POS,例如,从“有些青年人不是科学家”可以得出“有些科学家不是青年人”;但是,如果S类包含P类,P类是S的真子类,则从SOP不能得出POS。例如,从“有些年轻人不是北大学生”不能推出“有些北大学生不是人”[10]。SOP的谓项是否总是周延?这是一个值得考虑的问题,对它的不同回答会影响到对本文开头提到的那个难题的解决方案。我认为,在以上三种选择中,也许抛弃主项存在假定是最可行的,它能够消解那个难题,但也要付出很大的代价。
黑格尔说得好,熟知非真知。类似地,一个熟知的难题不一定就是一个已经得到解决的难题,也不一定是一个容易解决的难题。本文讨论的这个传统逻辑的难题就是如此。
[1]陈 波.直言命题的存在含义问题[J].湘潭师范学院学报,2003,(1):17-21.
[2]陈 波.逻辑学概论[M].北京:北京师范大学出版社,2007.
[3]郭世铭.周延性问题[J].自然辩证法研究,1997(增刊):25-29.
[4]金岳霖.逻辑[M].北京:三联书店,1961.
[5]Geach,P.T. “The Doctrine of Distribution”,in his Reference and Generality[M].Ithca,New York:Cornell University Press,1962,pp.3-21.
[6]Geach,P.T.“Distribution:aLastWord? ”,inhis Logical Matters[M].Berkeley and Los Angeles:University of California Press,1972,pp.62-64.
[7]Hurley,P.J.A Concise Introduction to Logic[M].Tenth edition,Thomson Wadsworth,2008.
[8]Mulder,D.H.“The Existential Assumptions of Traditional Logic”[J].History and Philosophy of Logic,17(1996),141-154.
[9]Parsons,T.“The Doctrine of Distribution”[J].History and Philosophy of Logic,27(2006),59-74.
[10]胡龙彪.论奥卡姆关于心灵语言指代的困难及可能的解决方法[J].湖南科技大学学报(社会科学版),2009,(6):29-33.
A Puzzle in Traditional Logic
LI Jian-hua1,CHEN Bo2
(1.School of Law,Hunan University of Science and Technology,Xiangtan,Hunan 411201,China;2.Department of Philosophy,Peking University,Beijing 100871,China)
There is a well-known puzzle in traditional logic,that is,SAP→SEP'→P'ES→P'AS'→S'IP'→S'OP,which is valid in its every step,but is not valid from the beginning to the end,for P is not distributive in the premiss SAP,but is distributive in the conclusion S'OP,which is against the rule of inference N.This result is made by the following three elements:the assumption of existence about the subject in catogorical propositions,the rule of inference N which says that if a term is not distributive in the premiss(es),then it must be not distributive in the conclusion,and the four regulations about the distribution of the subject and predecate in categorecal propositions.So,if we want to solve the puzzle,we have at least three choices:refutating the assumption of existence,revising the rule of inference N,and revising the regulations about distribution.Every choice has its own acceptable results and also unacceptable results,so it is not an easy choice.Therefore,the puzzle still awaits a final systematic solution.
categorical proposition;direct infernece;syllogism,assumption of existence;distribution
D091
A
1000-2529(2010)06-0019-05
2010-06-17
湖南省社会科学基金资助项目“当代自然逻辑研究”(09YBA064)
李建华(1953-),男,湖南涟源人,湖南科技大学法学院教授。陈 波(1957-),男,湖南常德人,北京大学哲学系教授,博士生导师。
(责任编校:文 建)

