关于 Diophantine方程 x3+1=111y2

刘 杰

（三明职业技术学院 ,福建三明 365000）

关于 Diophantine方程 x3+1=111y2

刘 杰

（三明职业技术学院 ,福建三明 365000）

应用递归序列、同余式证明了丢番图方程x3+1=111y2仅有整数解（x,y）=（-1,0）.

丢番图方程;整数解;递归数列;平方剩余

对于丢番图方程x3±1=Dy2（D>0）的整数解,曾有多人进行过研究,如曹珍富[1],柯召,孙琦[2]等人,但当D有 6k+1素因数时,方程求解较为困难,文献[3]讨论了方程x3+1=Dy2当 0100情形,则较少研究,特别当D既含 3因数又含6k+1形因数时要分多种情形讨论,研究更为繁难.笔者利用余模定向法[8]研究丢番图方程x3+1=111y2的整数解问题,其中 111既含有 6k+1因子,又含有 3的因子,证明了丢番图方程x3+1=111y2的全部整数解仅为（-1,0）.

引理 1[1]x2-3y4=1仅有整数解（x,y）=（±2,±1）,（±7,±2）,（1,0）,（-1,0）.

引理 2[1]4x4-3y2=1仅有整数解（x,y）=（1,1）,（-1,-1）,（1,-1）,（-1,1）.

1 主要结果

定理1 不定方程

仅有整数解（x,y）=（-1,0）.

证明 因为（x+1,x2-x+1）=1或 3,又111,所以不定方程（1）有下列 8种分解:

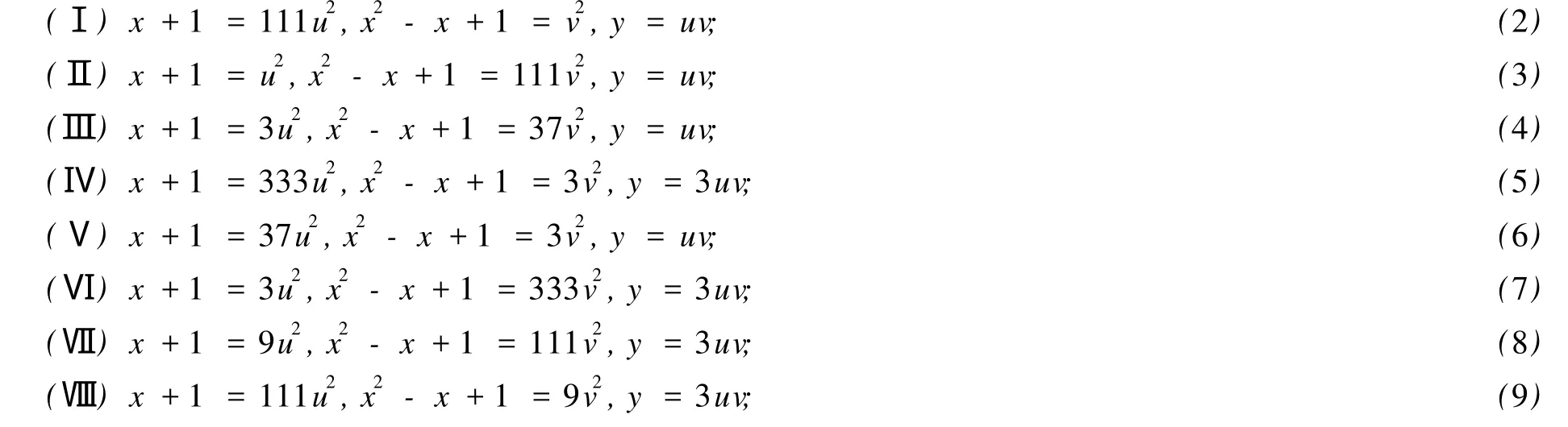
下面分别对 8种情形进行讨论.

（Ⅰ）此时分解方程为x+1=111u2,x2-x+1=v2,y=uv.

对于递归式（12）有

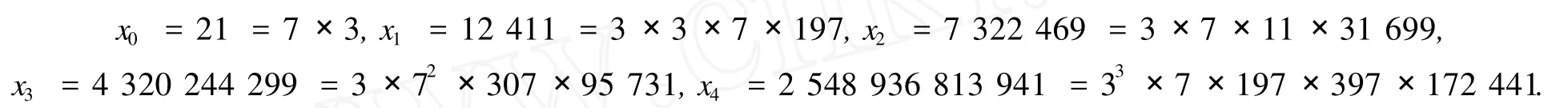
对于递归式（12）在 2u2=±Xn+3中,由于X-n-1=21U-n-1+222V-n-1=21（295Un+28×111Vn）-222（28Un+295Vn）=-21Un-222Vn=-Xn,故只要考虑 2u2=Xn+3,nZ,n≥0的情况.由（13）式2u2=21Un+222Vn+3显然有Xn≡（-5）n（mod 16）.

若n≡1（mod 2）,则Xn≡-5≡11（mod 16）,从而 2u2≡14（mod 16）即u2≡7（mod 8）不可能成立.

故n必须为偶数,

1）当n≡0（mod 4）时,Xn≡1（mod 10）.此时 2u2≡Xn+3≡4（mod 10）即u2=2（mod 5）也不可能成立.

2）当n≡2（mod 4）时,由（17）式有

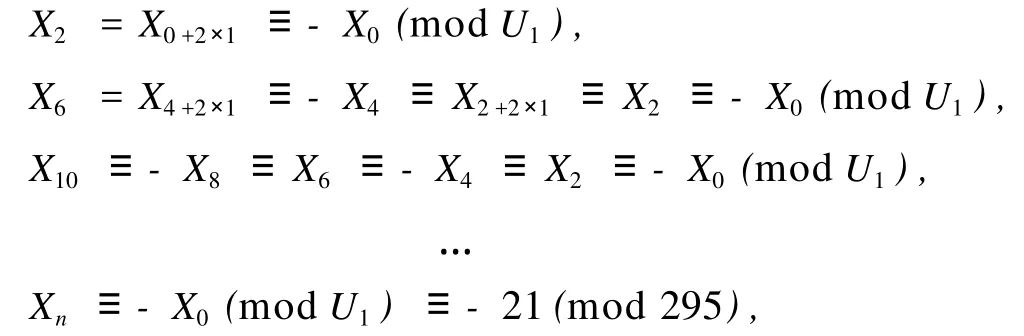
此时,2u2≡-Xn+3≡-21+3≡-18（mod 295）,据 jacobi符号法则,因为（2u2/295）=（2/295）= （-1）294×296/8=1,而（-18/295）=（-1/295）（2×32/295）=（-1）（2/295）=（-1）×1=-1矛盾.

故（Ⅱ）情形原方程无整数解.

（Ⅲ）此时分解方程为x+1=3u2,x2-x+1=37v2,y=uv.

解 对于x+1=3u2,x2-x+1=37v2,后式化为（2x-1）2-37（2v）2=-3,由x=3u2-1代入后得

2）现考虑n≡±1（mod 4）时情形,容易验证下列关系式成立:

①当n≡1（mod 4）时有Vn≡1（mod 8）,此时 222u2≡1+Vn（mod 8）≡2（mod 8）,即 3u2≡1（mod 4）不可能成立.

②当n≡-1（mod 4）时,设n=4m-1,则

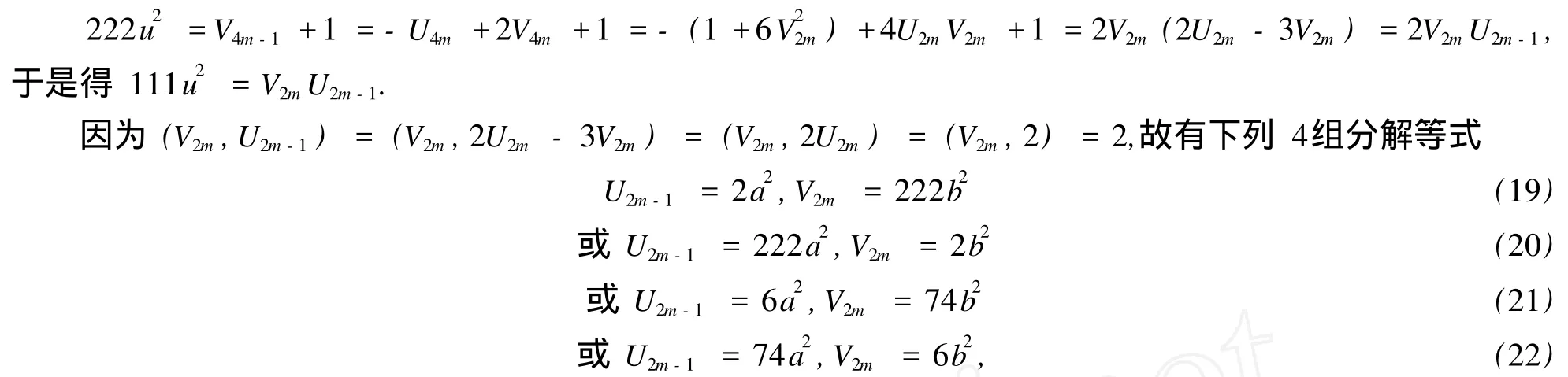
其中u=2ab.把（19）式的前式代入,由引理2得V2m-1=±1,即m=0或 1,但当m=1时,不适合（19）式的后式.而当m=0时,（19）式中b=0,从而u=0,这就给出了（1）式的平凡解（-1,0）.（20）式中V2m=2b2=2UmVm得UmVm=b2.因为（Um,Vm）=1,所以可设Um=c2, Vm=d2代入得c4-3（d2）2=1,据方程x4-Dy2=1[2]的结果有d=0,从而b=0,V2m=0,m=0,但不适合（20）式的前式,故（20）式无解.而（21）式的前式V2m-1≡2（mod 8）≠6a2≡6,0（mod 8）,故（21）式不成立.对于（22）式,由后式得V2m=6b2=2UmVm,即 3UmVm=9b2,于是Um=c2,3Vm= （3d）2,b=3cd,从而c4-3（3d2）2=1.据方程x4-Dy2=1的结果[2],必有d=0,从而b=0,V2m=0,得m=0,但不适合（22）式的前式,故此时无解.

综合以上各项讨论,这样（Ⅳ）就只有（1）式的平凡解（x,y）=（-1,0）.

（Ⅴ）此时分解方程为x+1=37u2,x2-x+1=3v2,y=uv.

下面对n≡1（mod 2）,即n≡±1（mod 4）情形进行讨论:

讨论情况完全与 （Ⅳ）的情形（2）相同,只要将这里的p看成u即可.于是得到（1）的平凡解（x,y）= （-1,0）.

（Ⅵ）此时分解方程为x+1=3u2,x2-x+1=333v2,y=3uv.

解 对于x+1=3u2,x2-x+1=333v2后式可化为（2x-1）2+3=333（2v）2,x=3u2-1代入得（6u2-3）2-37（6v）2=-3.

此时完全类似于（Ⅲ）的讨论得原方程无整数解.

（Ⅶ）此时分解方程为x+1=9u2,x2-x+1=111v2,y=3uv.

（Ⅷ）此时分解方程为x+1=111u2,x2-x+1=9v2,y=3uv.

解 对于x+1=111u2,x2-x+1=9v2后式化为（2x-1）2-9（2v）2=-3,把x=111u2-1代入得（222u2-3）2-（6v）2=-3,设X2-Y2=-3得X+Y=1,-3,X-Y=-3,1或X+Y=-1,3,XY=3,-1解得X=1,-1,从而x=0或 1都使得u,v无整数解,故原方程无整数解.

由以上 （Ⅰ）～（Ⅷ）的讨论知方程（1）仅有整数解 （-1,0）,定理证毕.

[1]曹珍富.丢番图方程引论[M].哈尔滨:哈尔滨工业大学出版社,1989.

[2]柯召,孙琦.谈不定方程[M].上海:上海教育出版社,1980.

[3]倪谷炎.关于不定方程x3+1=Dy2[J].哈尔滨师范大学学报:自然科学版,1999,36（3）:13-15.

[4]乐茂华.联立 Pell方程组的解数[J].吉首大学学报:自然科学版,2003,24（2）:1-9.

[5]罗明.关于不定方程x3+1=7y2[J].重庆师范学院学报:自然科学版,2003,20（1）:5-7.

[6]杨丽芬.关于丢番图方程x3+1=Dy2[J].哈尔滨师范大学学报:自然科学版,1995,32（4）:32-36.

[7]段辉明.关于不定方程x3+1=38y2[J].华东师范大学学报:自然科学版,2006（1）:35-39.

[8]刘杰.关于丢番图方程x3+1=201y2[J].佳木斯大学学报:自然科学版,2009,27（5）:761-763.

On the D iophantine Equationx3+1=111y2

L IU Jie

（SanmingVocational and Technical College,Sanming 365000,China）

In this paper,itwas proved that the Diophantine Equationx3+1=111y2has only integer solutions:（x,y）=（-1,0）.

Diophantine Equation;integer solution;recurrent sequence;guadratic remainder

O 156

A

1004-1729（2010）03-0205-04

2010-06-23

刘杰（1973-）,男,福建宁化人,三明职业技术学院讲师.