瓦斯浓度预测的混沌时序RBF神经网络模型

赵金宪, 于光华

(黑龙江科技学院 电气与信息学院,哈尔滨 150027)

瓦斯浓度预测的混沌时序RBF神经网络模型

赵金宪, 于光华

(黑龙江科技学院 电气与信息学院,哈尔滨 150027)

为对煤矿瓦斯质量浓度进行精确预测,针对瓦斯质量浓度的非线性特点,在验证其时间序列具有混沌特性的基础上,建立了基于混沌理论和径向基神经网络的预测模型。将实测瓦斯质量浓度时间序列进行相空间重构得到训练样本,并利用MATLAB仿真软件进行编程预测分析。结果表明,相对误差为 0～3%,均方差为 0.005 6,预测效果良好。实例验证该预测模型切实可行。

瓦斯质量浓度;混沌时间序列;神经网络;相空间重构

0 引 言

煤矿井下瓦斯分布是一个多维非线性系统,在生产实际中容易得到的只是瓦斯的时间序列[1]。影响瓦斯分布的因素众多 (如风速、温度和煤层等),仅仅以某一因素来预测矿井瓦斯质量浓度显然有很大的局限性。采用传统的线性方法如动力学方法和数理统计方法[2]建模,往往难以得到满意的结果。混沌理论为解决非线性问题提供了良好的方法。鉴于径向基(RBF)神经网络能够逼近任意的非线性函数,可以处理系统内在的难以解析的规律性,并且具有极快的学习收敛速度。笔者尝试采用混沌理论与 RBF神经网络相结合来建立预测模型。

1 混沌判定

在建立混沌时间序列预测模型前需要判断该序列是否具有混沌特性。判断方法通常为时域分析法、频谱分析法和 Lyapunov指数法[3]。其中,Lya-punov指数法反映了混沌动力学系统对初始条件的敏感依赖性,最大Lyapunov指数大于 0,意味着轨道局部不稳定,说明系统有混沌特性[4]。文中采用Lyapunov指数法对其进行判断,通过小数据量方法来计算最大 Lyapunov指数。该方法具有对小数据组可靠、计算量小、操作方便等优点。具体步骤为:

(1)对时间序列{x1,x2,…,xN}进行傅里叶变换,计算出平均周期P。

(2)计算出时间延迟τ,嵌入维数m。

(3)根据τ和m重构相空间{Yj,j=1,2,…,M}。

(4)找相空间中每个点Yj的最近邻近点Yj^,并限制短暂分离,即

(5)计算出Yj邻点对的i个离散时间步后的距离dj(i):

其中,q是非零dj(i)的数目,并用最小二乘法作出回归直线,该直线的斜率就是最大Lyapunov指数λ。

2 相空间重构参数选择

相空间重构的目的是在高维相空间中恢复混沌吸引子。混沌吸引子作为混沌系统的特征之一,体现混沌系统演化的普适性,意味着混沌系统产生的轨迹在经过一段时间演化后,最终会呈现一定的规律。根据这一特性就能由系统的当前状态获得下一时刻的状态,从而得到时间序列下一时刻的预测值。以复杂的瓦斯质量浓度时间序列为研究对象,根据Packard[5]和 Takens[6]提出的通过找到合适的m和τ,来重构相空间

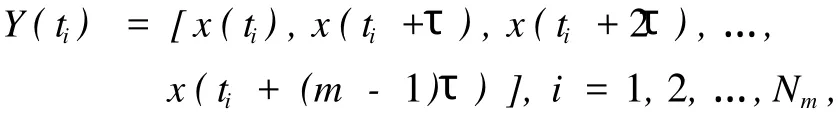
以便把时间序列中蕴藏的信息充分显露出来。重构相空间的关键在于τ和m的选取。

2.1 延迟时间

延迟时间是相空间重构中的一个重要参数,其选取是很困难的。最佳延迟时间τ既不能太大也不能太小,当τ选择的太小时,延迟矢量各坐标值间有很强的相关性,信息不容易泄露。当τ太大时,重构矢量各坐标值间的关系几乎变成随机的,破坏了原系统各变量间的内在关系,使得重构矢量包含的原动力系统信息丢失。考虑到瓦斯时间序列间的非线性特性,笔者采用包含了非线性特征的互信息量法[7]。

Shaw首先提出以互信息第一次达到最小时的滞时作为相空间重构的时间延迟,Fraser给出了互信息计算的递归算法[2],是可从事件bj在序列B中发生的概率中得到多少关于ai在序列A中发生概率的信息称为A和B间的平均互信息。记时间序列[a, b]=[x(t),x(t+τ)],则互信息函数为

计算互信息的困难在于从直方图中估计分布PAB,通常采用划分网格的方法,τ取互信息函数的第 1个极小值。

2.2 嵌入维数

嵌入维数m是相空间重构中的又一重要参数。若m选择的太小,吸引子将被折叠,重构相空间不能准确地反映时间序列的混沌特性;若m太大,不仅会降低重构相空间的质量,增加程序运行时间,且噪声有可能占主导地位。目前,常用的最佳嵌入维数的选取方法有 G-P方法、预测误差最小法和 Cao氏法[8]。文中采用 G-P方法,具体步骤为:

(1)取已计算出来的τ,并从m=2开始对时间序列{x(ti),i=1,2,…,N}重构相空间。

(2)计算重构相空间{Y(ti)}关联函数,

其中,表示相点Y(ti)和Y(tj)间的距离,θ(z)是 Heaviside函数,C(r)是一个累积分布函数,表示相空间中吸引子上两点间距离小于r的概率。

(3)恰当地选取r值,关联维数d与C(r)应满足对数线性关系,即d(m)=lnC(r)/lnr。从而由拟合求出对应于m的关联维数估计值d(m)。

(4)不断增加m,重复步骤(2)、(3),直到相应的d(m)不再随m增长,而在一定误差范围内不变为止。此时维数达饱和嵌入维数。

3 神经网络预测

鉴于神经网络的并行处理及强大的非线性映射能力[9],对于未知的动力系统,可以通过它来学习混沌时间序列,进行预测和控制。由于混沌时间序列在内部有着确定的规律性,这种规律性产生于非线性特性,它表现出时间序列在时间延迟状态空间中的相关性,这种信息处理方式正好是神经网络所具备的。著名的 Klomogorov连续性定理从数学上证明了神经网络用于混沌时间序列预测的可行性[2]。通过建立相应的神经网络模型,进而实现瓦斯质量浓度的准确预测,预测模型如图 1所示。

图1 瓦斯浓度预测模型Fig.1 Gas concentration predictability model

RBF神经网络结构简单、训练简洁且学习收敛速度快,能够逼近任意非线性函数。在时间序列分析中具有较广泛的应用[10]。文中采用该方法的具体步骤为:

(1)将给定的时间序列x1,x2,…,xN,…,xN+T后T个数据Ti(xN+1,xN+2,…,xN+T)作为要预测的数据,即为预测步长T。对前N个数据,根据 G-P算法求得最优嵌入维数m,互信息量法计算τ,并重构相空间{Y(ti)}。

(2)将Y(ti)中的前N个点作为训练样本,其余点为测试样本。

(3)构建神经网络用训练样本进行训练,通过调节RBF网络的 SPREAD参数,来确定网络的最佳结构状态,用来测试预测模型从而获取对应的预测值。

4 实例分析

笔者选择某矿区 2002年 1月份实际生产瓦斯质量浓度数据,采样时间间隔 1 h,共 744个数据,从中提取 360个作为试验样本,如图 2所示。

图2 煤矿瓦斯质量浓度数据Fig.2 Coalm ine gas concentration data

4.1 判别混沌的存在

根据第 1部分提到的小数据量法计算序列最大Lyapunov指数λ,经MATLAB编程得该序列的λ= 0.114 9,由于λ>0,可判断该序列具有混沌特性。

4.2 相空间重构

根据第 2部分介绍的理论重构相空间

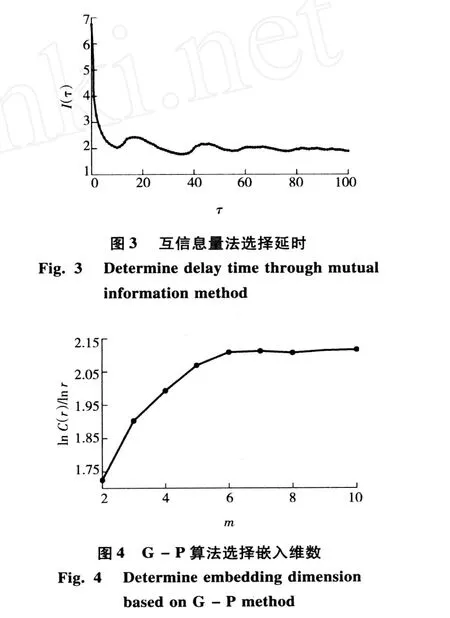
其中用互信息量法计算延迟时间,从图 3中可看出τ=10。由 G-P算法分析,从图 4中可得嵌入维数m=6。

4.3 混沌理论与神经网络预测

根据上述计算得出的嵌入维数m=6作为神经网络的输入层节点数,预测步长取 60,对前 300个样本进行相空间重构,共得到 250个相点,其中 190个作为神经网络的训练样本,60个为测试样本。

用 RBF神经网络对重构后的时间序列进行预测,确定输入层的神经元个数为 6,输出层神经元为1,经反复改变确定 SPREAD参数为 3,网络创建函数为 newrb,中间层神经元个数最大值为 200,训练目标设定为 0.001,经过 15次训练后,网络达到要求(图 5)。由于篇幅有限文中仅给出一天 24 h的数据分析。图 6为 24 h预测值与真实值比较。经分析模型的均方差为 0.005 6,相对误差控制在 0～ 3%(图 6),证明混沌理论与 RBF神经网络结合效果较好,能够满足生产现场的实际需求。

5 结束语

笔者利用混沌时间序列方法对煤矿瓦斯质量浓度时间序列进行分析,计算得出λ=0.114 9>0,表明该序列具有混沌特性。通过 RBF神经网络对单变量序列进行预测,减少了复杂的编程过程。以已知的瓦斯质量浓度数据为样本,利用文中提出的模型研究瓦斯质量浓度预测,实验结果表明该模型具有较高的预测精度,在保障井下工作人员和设备安全方面有重要的应用价值。但混沌时间序列分析方法步骤繁多,有些理论和方法还需进一步研究。

[1] 林柏泉,崔恒信.矿井瓦斯防治理论与技术[M].徐州:中国矿业大学出版社,1998.

[2] 吕金虎,陆君安,陈士华.混沌时间序列分析及其应用[M].武汉:武汉大学出版社,2002.

[3] 高 莉,胡延军,于洪珍.基于W-RBF的瓦斯时间序列预测方法[J].煤炭学报,2008,33(1):67-70.

[4] 陈 敏,叶晓舟.混沌时间序列的判定方法研究[J].信息技术,2008,32(6):22-25,54.

[5] PACKARD N H,CRUTCHFIELD J P,FARMER J D,et al.Geometry from a time series[J].Physical Review Letters,1980,45(9): 712-716.

[6] TAKENS F.Detecting strange attractors in turbulence[M].Heidelberg:SpringerBerlin,1981.

[7] 程 健,白静宣,钱建生,等.基于混沌时间序列的煤矿瓦斯浓度短期预测[J].中国矿业大学学报,2008,37(2):231-235.

[8] 孙 艳.基于混沌时间序列和神经网络的电力短期负荷预测[D].南宁:广西大学,2007.

[9] 葛哲学,孙 志.神经网络理论与MATLABR2007实现[M].北京:电子工业出版社,2008.

[10] 高 隽.人工神经网络原理及仿真实例[M].北京:机械工业出版,2005.

Modelof chaotic sequence and RBF neural network on gas concentration forecast

ZHAO Jinxian,YU Guanghua
(College of Electric and Infor mation Engineering,Heilongjiang Institute of Science and Technology,Harbin 150027,China)

Directed at the accurate prediction of the coal gas concentration,this paper proposes a chaos theory and RBF neural ne twork-forecastingmodel,established according to the nonlinear characteristics of gas concentration and the validated chaotic characteristics of time series for gas concentrations. The reconstruction of the gas concentration time series for the training samples and the use ofMATLAB simulation to forecasting analysis show that the relative prediction error ranging from 0 to 3%and the mean square error of 0.005 6 justify the feasibility of prediction model.

gas concentration;chaotic time series;neural ne twork;phase space reconstruction

TD712.53;TP183

A

1671-0118(2010)02-0131-04

2009-09-18;

2010-02-08

黑龙江省研究生创新科研项目(YJSCX2009-066HLJ)

赵金宪(1970-),男,吉林省舒兰人,教授,硕士,研究方向:计算机过程控制,E-mail:zjx5579@163.com。

(编辑王 冬)