一类非负矩阵对的本原指数

罗美金,侯宗毅

(河池学院 数学系,广西 宜州 546300)

一类非负矩阵对的本原指数

罗美金,侯宗毅

(河池学院 数学系,广西 宜州 546300)

研究了一类特殊的双色有向图,它的未着色图中含有 3n-2个顶点,包含一个(2n+1)-圈和一个n-圈的图,给出了本原条件和指数的上、下界,并对极图进行了刻划.

本原指数;本原图;双色图;指数界;极图

0 引言

设D是一个有向图,D的一条长为l的途径是指连续的顶点序列v1,v2,……,vl+1,其中对所有的i=1,2,……,l,D中都有从vi到vi+1的弧.如果v1,v2,……,vl+1,互不相同,则称该途径是一条长为l的路.如果vi=vi+1,则称为一条闭路或圈.如果D是包含红弧和蓝弧的有向图,则称D是一个双色有向图[1].

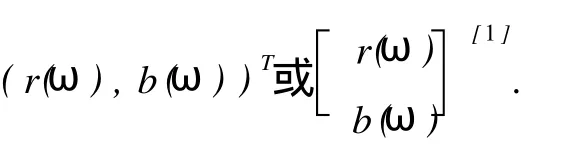
非负矩阵对(A,B)同样与其伴随有向图存在一一对应关系,其伴随有向图记为D(A,B),显然D(A,B)具有顶点 1,2,……,n.非负矩阵对与其伴随有向图建立了对应关系,即可从非负矩阵对(A,B)中元素的数值来判断其伴随有向图D(A,B)中对应弧存在与否.如:从矩阵A=(aij)中元素的数值可判断D(A,B)中是否存在对应的红弧,若aij>0,则从顶点i到顶点j存在一条红弧;同样从矩阵B=(bij)中元素的数值可判D(A,B)中是否存在对应的蓝弧,若bij>0,则从顶点i到顶点j存在一条蓝弧[2].

如果双色有向图对应的非负矩阵对(A,B)是本原的,则称双色有向图D(A,B)是本原的,且D(A,B)的本原指数 exp(D(A,B)),即为(A,B)的本原指数 exp(A,B).由非负矩阵对的本原性及其本原指数的概念,可将双色有向图的本原性及其本原指数的概念定义为:

一个双色有向图D是本原的,当且仅当存在非负整数h和k,且h+k>0,使得D中的每一对顶点(i,j)都存在从i到j的(h,k)—途径,h+k的最小值定义为双色有向图D的本原指数,记为 exp(D).(h,k)—途径是指从i到j的途径中包含h条红弧和k条蓝弧[3].

引理 1:[4]一个至少包含一条红弧和一条蓝弧的双色有向图D是本原的,当且仅当D是强连通的,且content(M)=1.

目前对双色本原有向图(非负本原矩阵对)的研究只得到了一些初步的结果.在国内,关于非负本原矩阵对的研究也取得了一些成果[1,2,3,5,6,7].本文研究一类特殊的双色有向图D,它的未着色有向图如图1所示.

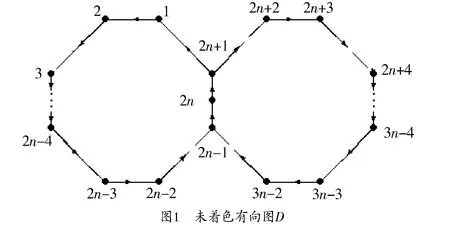
显然,D中仅包含两个圈,圈长分别为 2n+1和n,且两个圈有公共弧 2n-1→2n→2n+1,则D的圈矩阵可写为

其中a,b为正整数.

1 本原条件

=1,且

定理 1: 双色有向图D是本原的,当且仅当an-b(2n+1)

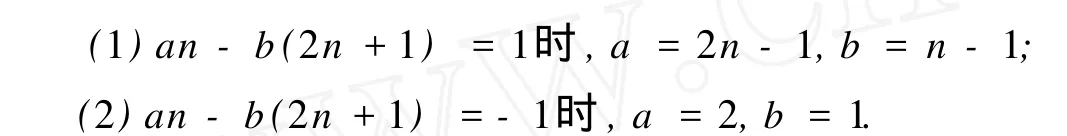
证明:显然,D是强连通的,det(M)=an-b(2n+1),故由引理1得,D是本原的当且仅当 det(M)=±1,要使a,b都为正整数,容易验证,当an-b(2n+1)=1时,a=2n-1,b=n-1;当an-b(2n+1)=-1时,a=2,b=1.定理得证.

2 指数上界

定理 2: 设双色有向图D是本原的,且an-b(2n+1)=1,则 exp(D)≤12n2-12n-4.

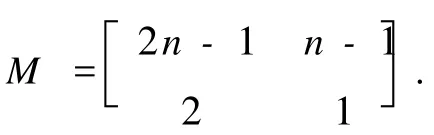
类型一:弧 2n-1→2n→2n+1不包含蓝弧.

只需证明对D的任意一对顶点(i,j),都有一条(12n2-24n+11,12n-15)-途径.取ρ1=3n-4-s+(n-1)t,ρ2=3(2n-1)-4+2s-(2n-1)t.因此,从顶点i出发,沿pij到顶点j,转(2n+1)-圈ρ1次,转n-圈ρ2次的途径有分解

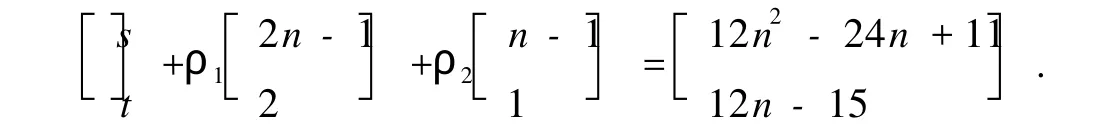
显然,s≤3n-4,t≤3且ρ1≥0,ρ2≥0.当s=3n-4时,t≥0;t=3时,s≥2.此时,ρ1=0或ρ2=0时,Pij必包含公共弧 2n-2→2n→2n+1.所以

exp(D)≤12n2-24n+11+12n-15=12n2-12n-4.

类型二:弧 2n-1→2n→2n+1包含一条蓝弧.

只需证明对D的任意一对顶点(i,j),都有一条(10n2-17n+6,10n-9)—途径.取ρ1=3n-4-s+(n-1)t,ρ2=2(2n-1)+2s-(2n-1)t.因此,从顶点i出发,沿Pij到顶点j,转(2n+1)圈 ρ1次,转n-圈ρ2次的途径有分解

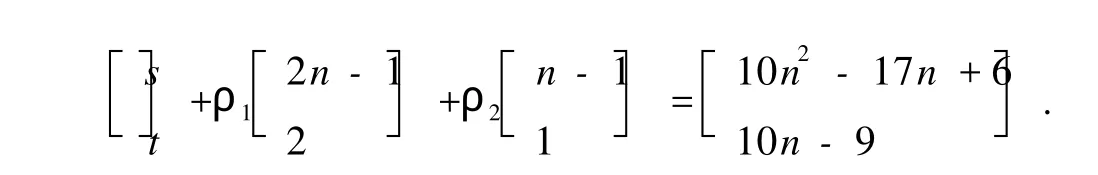
显然,s≤3n-3,t≤2,且ρ1≥0,ρ2≥0.当s=3n-3时,t≥1;t=2时,s≥0.此时,Pij必包含公共弧 2n-1→2n→2n+1.所以

exp(D)≤10n2-17n+6+10n-9=10n2-7n-3.

类型三:弧 2n-1→2n→2n+1包含两条蓝弧.

只需证明对D的任意一对顶点(i,j),都有一条(8n2-12n+4,8n-6)-途径.取ρ1=3n-4-s+(n-1)t,ρ2=2(2n-1)+2s-(2n-1)t.因此,从顶点i出发,沿Pij到顶点j,转(2n+1)-圈ρ1次,转n-圈ρ2次的途径有分解

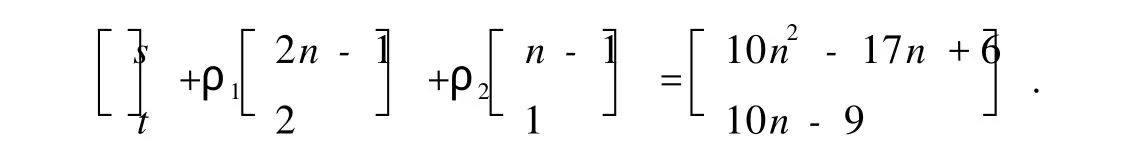
显然,s≤3n-2,t≤2,且ρ1≥0,ρ2≥0.当s=3n-2时,t=2;t=2时,s≥0.此时,Pij必包含公共弧 2n-1→2n→2n+1.所以

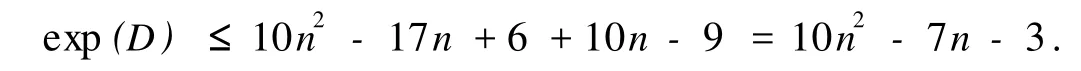
比较类型一、二、三 exp(D)的大小,显然得 exp(D)≤12n2-12n-4.定理得证.

定理 3: 设双色有向图D是本原的,且an-b(2n+1)=-1,则 exp(D)≤12n2-12n-4.

证明:与定理 2类似可证.

3 指数下界

定理 5: 设双色有向图D是本原的,且an-b(2n+1)=-1,则 exp(D)≥4n2+n.

证明:与定理 4类似可证.

4 指数上界的极图刻划

定理 6: 设双色有向图D是本原的,且an-b(2n+1)=1,则 exp(D)=12n2-12n-4当且仅当D中存在一条 3n-4长的红路.

证明:充分性:由定理 3,只需证明 exp(D)≥12n2-12n-4.

必要性:利用反正法.设双色有向图D是本原的,且an-b(2n+1)=1.若不存在一条 3n-4长的红路,只需证明 exp(D)<12n2-12n-4即可.

只需证明对D的任意一对顶点(i,j),都有一条(12n2-26n+12,12n-17)-途径.取ρ1=3n-5-s+(n-1)t,ρ2=3(2n-1)-4+2s-(2n-1)t.因此,从顶点i出发,沿Pij到顶点j,转(2n+1)-圈ρ1次,转n-圈ρ2次的途径有分解

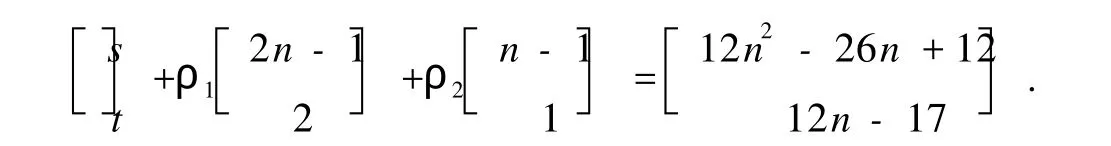
显然,s≤3n-4,t≤3且ρ1≥0,ρ2≥0.当s=3n-4时,t≥1;t=3时,s≥2.此时,ρ1=0或ρ2=0时,Pij必包含公共弧 2n-1→2n→2n+1.所以,

exp(D)≤12n2-26n+12+12n-17=12n2-14n-5<12n2-12n-4.定理得证.

定理 7: 设双色有向图D是本原的,且an-b(2n+1)=-1,则 exp(D)=12n2-12n-4当且仅当D中存在一条 3n-4长的蓝路.

证明:与定理 6类似可证.

5 指数下界的极图刻划

定理 8: 设双色有向图D是本原的,且an-b(2n+1)=1,则 exp(D)=4n2-3n-1当且仅当D中(2n+1)-圈上同时存在两条连续红路,路长分别为n-1和n.

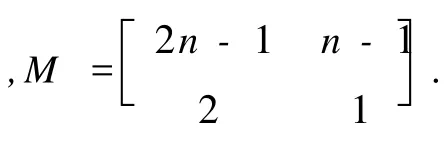
类型一:弧 2n-1→2n→2n+1不包含蓝弧.

只需证明对D的任意一对顶点(i,j),都有一条(4n2-3n,4n)-途径.取ρ1=n-s+(n-1)t,ρ2=2n+2s-(2n-1)t.因此,从顶点i出发,沿pij到顶点j,转(2n+1)-圈ρ1次,转n-圈ρ2次的途径有分解

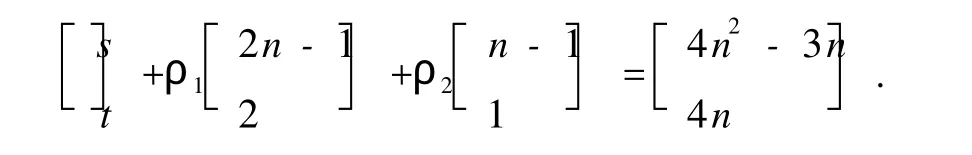
考虑以下两种情形:

情形 1 顶点i到顶点j在(2n+1)-圈上,且不包含n-圈上的点.此时,0≤s≤2n-4,0≤t≤2.

i)当t=0时,0 ≤s≤n,ρ1≥0,ρ2>0;

ii)当t=1时,0 ≤s≤2n-4,ρ1>0,ρ2>0;

iii)当t=2时,n-1 ≤s≤2n-5,ρ1>0,ρ2≥0.

情形 2 顶点i到顶点j上包含n-圈上的点.此时,0≤s≤3n-4,0≤t≤3.显然,满足ρ1≥0,ρ2≥0.

故对D的任意一对顶点(i,j),都有一条(4n2-7n+3,4n-4)-途径.当ρ1=0或ρ2=0时,必含弧2n-1→2n→2n+1.所以

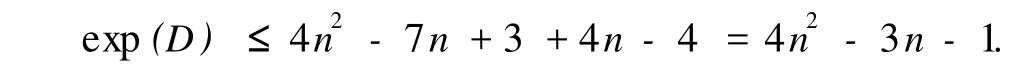
类型二:弧 2n-1→2n→2n+1包含一条蓝弧.

类型三:弧 2n-1→2n→2n+1包含两条蓝弧.

类型二、三与类型一类似可证.

综上所述得 exp(D)≤4n2-7n+3+4n-4=4n2-3n-1.定理得证.

定理 9:设双色有向图D是本原的,且an-b(2n+1)=-1,则 exp(D)=4n2+n当且仅当D中(2n+1)圈上同时存在两条连续蓝路,路长分别为n-1和n.

[1]罗美金,高玉斌.一类双色有向图的本原指数[J].中北大学学报 (自然科学版),2008,29(2):95-100.

[2]Shao Yanling,Gao Yubin,Liang Sun.Exponents of a class of two-colored digraphs[J].LinearAlgebra and itsApplacations,2005,(53):175-188.

[3]Gao Yubin,Shao Yanling.Exponents of two-colored digraphswith two cycles[J].LinearAlgebra and itsApplacations,2005,(407):263-276.

[4]B L Shader,S Suwilo Exponents of nonnegative matrix pairs[J].LinearAlgebra Appl.,2003,(363):275-293.

[5]罗美金,高玉斌.一类恰含三个圈的三色有向图的本原指数[J].山东大学学报 (理学版),2008,43(1):65-72.

[6]罗美金,高玉斌.一类含有两个圈的双色有向图本原指数[J].中北大学学报 (自然科学版),2007,(5):377-382.

[7]汪荣,邵燕灵,高玉斌.一类双色有向图本原指数的上界[J].吉林大学学报 (理学版),2008,(4):601-606.

The Exponent of a Class of NonnegativeMatrix Pa irs

LUO M ei-jin,HOU Zong-yi

(Depart ment ofMathematics,Hechi Un iversity,Y izhou,Guangxi546300,China)

In this article,we study a type of special two-colored digraphs whose uncolored digraph has 3n-2 vertices and consists of one(2n+1)-cycle and one n-cycle.We give some primitive conditions and the bound on the exponents.Finally,we give the characterizations of extremal two-colored digraphs.

exponent;primitive digraph;two-colored digraph;bound;extremal digraph

O157.5

A

1672-9021(2010)02-0015-05

罗美金 (1981-),女,江西广丰人,硕士,河池学院数学系教师,主要研究方向:组合数学.

河池学院《应用数学》重点学科 (200725)

2010-3-20

[责任编辑普梅笑 ]