关键函数和辅助函数——解决积分运算的一种思想
王信存
(辽东学院师范学院 高等数学教研部,吉林 丹东 118003)
2.3.2 关键函数存在,辅助函数需要构造
解这种类型题的关键是对基本积分公式是否熟悉,是否掌握出题者所考查的知识点 .
2.3.3 需要将原题适当变形,析出关键函数和复合函数
解析:回忆微分运算公式的产生过程,会发现 (sinx)′=cosx,(cosx)′=-sinx,是直接运用定义得出的公式 .后在教材中给出了四则运算的求导法则,其中除法的运算法则为
即三角函数主要的导数公式是以正弦、余弦为基础的 .因为积分运算和微分运算是互逆运算,所以要进行正切的积分运算,可以尝试化为熟悉的正、余弦公式 .
关键函数和辅助函数
——解决积分运算的一种思想
王信存
(辽东学院师范学院 高等数学教研部,吉林 丹东 118003)
提出关键函数和辅助函数的概念,举例说明它们在不同积分运算方法中所起的作用,并对不同形式的关键函数和辅助函数做了分类叙述 .
关键函数;辅助函数;积分运算
0 引言
本文先从教材的第一类换元积分基本定理出发,通过例题对定理进行解释说明,进而提出关键函数和辅助函数的概念 .对出现关键函数和辅助函数的不同形式进行详细研究,通过不同类型题的求解,充分认识到这种理解方式的重要性,指出这种思想在其它积分方法中的应用,以望快速准确地解决此类问题 .
1 教材中关于第一类换元积分法的定理及解释
先从基本定理来了解一下 .

注意到把被积函数与基本积分公式对照,确认了正弦函数的基本积分公式,然后使两者的积分变量一致 .而为了被积函数变量和积分变量的一致,将 exdx凑成 dex,故也称作凑微分法 .
2 关键函数在第一类换元积分法中的应用
为了更好地把握定义,熟练使用该方法,下面提出关键函数和辅助函数的概念 .
2.1 关键函数和辅助函数的提出
第一类换元积分法所能解决的积分问题中其实都隐含着关键函数和辅助函数,所谓的关键函数就是指要考察的基本积分公式所对应的被积函数,因为被积函数的出现形式都是复合函数,所以为了将被积函数积出,必须将变量保持一致,为此应该存在辅助函数,即辅助函数存在的目的是为了关键函数的积出[3].下面举例说明:

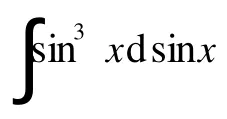
2.2 关键函数和辅助函数的确定原则
(1)关键函数一般都是复合函数 .
(2)同类型的函数,相对复杂的作为关键函数 .
(3)不同类型的函数乘积作被积函数时,对数函数和反三角函数容易成为关键函数,指数函数和三角函数容易成为辅助部分 .
(4)幂函数与其他函数乘积作被积函数时,幂函数遇到对数和反三角函数时容易成为辅助函数,而当它遇到三角函数和指数函数时则很可能成为关键函数 .
(5)根式一般都是关键函数[2].
下面举出相应的例子 .



2.3 关键函数和辅助函数出现的不同形式
对于换元积分的运算而言,关键函数和辅助函数的提出是一种分析问题的创新思维方式,对于不同的习题,它们的存在方式也不尽相同 .



2.3.2 关键函数存在,辅助函数需要构造
解这种类型题的关键是对基本积分公式是否熟悉,是否掌握出题者所考查的知识点 .
2.3.3 需要将原题适当变形,析出关键函数和复合函数
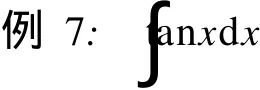
解析:回忆微分运算公式的产生过程,会发现(sinx)′=cosx,(cosx)′=-sinx,是直接运用定义得出的公式 .后在教材中给出了四则运算的求导法则,其中除法的运算法则为

即三角函数主要的导数公式是以正弦、余弦为基础的 .因为积分运算和微分运算是互逆运算,所以要进行正切的积分运算,可以尝试化为熟悉的正、余弦公式 .
即先将原式转化

2.3.4 关键函数和辅助函数都不完整,巧妙构造将它们补全

此题的关键函数和辅助函数都是构造因式补充完整的,算是一类特殊的习题,很考验我们的数学思维 .
3 关键函数在第二类换元积分法中的应用

4 在分部积分法中的关键函数

可以看出,分部积分法的关键是确定哪个函数为u,哪个部分为 dv,选择恰当,可以使函数的求解事半功倍,但如果选择不恰当,可能反而会使函数变得更为复杂 .其实这里的u可以理解为本文提出的关键函数,而 dv一般是由辅助函数和凑微分得到 .

这样右端的不定积分显然比左端更难求 .
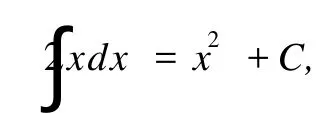



5 结论
关键函数和辅助函数并不是一种严格定义,而是解决积分运算的一种新的思想,这种思想的有效运用确实对积分运算产生了重要作用,在高等数学这样的高度抽象的学科中,创造性的运用一些新的思维方式理解问题、分析问题,或许是大学生,尤其是高职学生学好高等数学课的一个新途径 .
[1]新世纪高职高专教材编审委员会.新编高等数学[M].大连:大连理工大学出版社,2004.
[2]王信存.复合函数的整体化思维[J].大庆师范学院学报,2008,(2):86-88.
[3]王信存.一种新的函数分类方法—分部积分法中关键函数的确定[J].宜宾学院学报,2008,(6).
Key Function and Assistance Function——A Tra in of Thought of Solving Integration Calculation
WANG X in-cun
(Eastern L iaon ing Un iversity Normal College,Dandong,Jil in 118003,China)
This paper defines the conceptsof key function and assistance function and uses examples to explain their functions in integration calculation and classifies the different fcr ms of key function and assistance function.
key function;assistance function;integration calculation
O174
A
1672-9021(2010)02-0004-05
王信存 (1973-),男,辽东丹东人,辽东学院师范学院高等数学教研部讲师,硕士,主要研究方向:数值逼近与数字图像处理 .
辽宁省十一五教育科学规划课题 (职教 32—14)
2009-12-10
[责任编辑普梅笑 ]

