企业知识产权交易定价的博弈分析
刘卫国,李乾文
(南京审计学院 管理学院,南京 211815)
企业知识产权交易定价的博弈分析
刘卫国,李乾文
(南京审计学院 管理学院,南京 211815)
知识产权定价过程是买卖双方讨价还价的博弈过程,文章以博弈理论为基础,尝试构建了知识产权交易博弈模型并进行了简单分析,指出在知识产权交易非重复博弈中,买卖双方存在五种可能的博弈结果,最后给出知识产权质量高或质量低时,卖方选择定高价或定低价出售的判断标准。
知识产权;信号博弈;定价;博弈分析
现实生活中,买卖双方在进行知识产权交易时,价值只是交易的一张底牌,最后成交价格的确定则是买卖双方讨价还价(博弈)的结果。事实上作为一种市场经济行为,知识产权交易实质上是买卖双方在追求各自利益最大化前提下所进行的信号博弈行为。因此用博弈论的思想方法去分析知识产权交易定价就显得非常必要,这对于提高知识产权交易的理性,引导并规范知识产权交易市场健康、稳定发展具有深远的意义。
1 知识产权价值确定的传统方法
国内外经济学论著中介绍的知识产权价值确定方法有很多,但是这些方法在逻辑上大体可以分为三种基本类型,通常称为收益现值法、成本法和市场法。
1.1 收益现值法
收益现值法是将知识产权在使用年限内带来的未来净收益按照一定折现率折现的总价值作为知识产权价值。其基本计算公式如下:
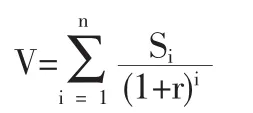
式中:V表示为知识产权评估价值;Si表示第i年的知识产权收益预测值;n表示知识产权的寿命期;r表示折现率。
收益现值法是把被评估知识产权剩余寿命期间内的预期未来收益,按照一定的贴现率,折成现值,来确定被评估知识产权价格的方法。因此,它只适用于直接产生收益的经营性资产,该类资产通过生产经营带来收益,同时通过生产经营的进行,其在若干个会计期间内会连续不断地创造出收益。知识产权属于生产要素或称经营性资产,其价值是通过对知识成果的利用而产生或预期产生的收益,因此,对知识产权价值评估最为适当的方法应为收益现值法。国外学者Reilly和 Dandekar曾对包括知识产权在内的各类无形资产评估的适用方法作过较详细的分类,其研究成果显示,已批准的专利、商标与商誉、版权(计算机软件除外)的评估主要都是采用收益现值法[1]。
1.2 市场价值法
市场价值法是通过市场调查,选择一个或几个与评估对象相同或类似的资产作为比较对象,针对各项价值影响因素,分析比较对象的成交价格和交易条件,将被评估资产与比较对象逐个进行对比调整,估算资产价值的方法。市场价值法只有存在与被评估资产相类似的资产交易市场时才适用。由于知识成果具有新颖性、创造性,一般不会出现完全相同的知识成果。另外,我国企业从20世纪90年代才开始逐渐重视知识产权,知识产权的交易也就经历了不到20年的时间,不仅交易的历史短,交易的数量也不多,说明了可使用的知识产权交易的历史资料是有限的。因此,在运用市价价值法对知识产权进行评估时,由于对某些知识产权获取市场信息的局限性,评估人员很难找到比较合适的历史可比资料,转而求其次。这样难免会造成评估结果的失真。但是在条件适当的情况下,采用市场法确定知识产权的价值也是一种较可行的方法。
1.3 重置成本法
重置成本法是以重新建造或购置与被评估资产具有相同用途和功效的资产现时需要的成本作为计价标准。其基本原理是按重置成本价格对知识产权进行估价,即按照评估知识产权全新状态的重置成本减去该项产权功能性贬值和经济性贬值估算知识产权价值的方法。由于知识产权价值的特殊性,应用成本法评估其价值存在很大障碍。例如,对技术商品而言,其生产过程是高度复杂的脑力劳动过程,具有探索性和创造性,不像一般商品的生产可以进行模式化劳动;对专利而言,由于专利只授予首先申请发明的人,如果被人捷足先登,即使耗费很大也是前功尽弃。或即便取得专利,很快又有人开发出更先进的取代技术,也收不到预期效益;对于商标而言,要想找到商标的重置成本是困难的。由于这些问题的存在,在使用重置成本法确定知识产权的重置成本时,很难保证评估结果不失真。因此,一般情况下,重置成本法不宜作为评估知识产权的方法。
总的来讲,采用收益现值法、市场价值法和重置成本法确定知识产权价格的方法要么是从买卖双方其中某一方角度考虑问题,要么是从市场的角度考虑问题,都不是非常全面,笔者认为知识产权交易价格应该通过买卖双方讨价还价的过程确定。
2 知识产权交易定价博弈模型构建
在知识产权交易活动中,买卖双方的交易行为显然是一种博弈行为:一方面,由于买卖双方信息不对称的存在,该博弈是不完全信息博弈;另一方面,整个交易过程经过报价、成交实施或追究违约责任等过程,该博弈还可以看成是动态博弈。
2.1 基本假设
博弈中的主要参与人是知识产权交易双方。为了简便分析,本文仅使用交易双方作为参与人构建博弈模型,并做出如下假设:
⑴假设知识产权交易成功与否只取决于参与博弈的买卖双方,知识产权制度、知识产权市场状况、知识产权关系等作为外部因素暂不考虑。
⑵假设参与人都是理性的,严格追求自身利益最大化,因而具有进行交易获取潜在收益的动力。
⑶假设知识产权有质量高、低两种情况,买方估计这两种情况能产生的未来现金流的现值分别Vg和Vb,且Vg>Vb。同时,卖方知识产权的质量信息属于私人信息,买方只知道卖方的定价,只能根据卖方的定价来判断知识产权的质量,即对卖方知识产权的质量具有不完全信息。
⑷假设买方的全部可选策略包括买或不买,卖方的全部可选策略包括定高价或定低价,分别用Ph和PI表示,且Ph>Pl。卖方在知识产权质量高时可以选择高定价或低定价,而且在知识产权质量低时同样也可以选择高定价或低定价。卖方对质量高、低的知识产权付出的努力成本分别为Ch和CI;C1为卖方对质量低的知识产权选择定高价时所花费的包装成本;C2为质量低的知识产权定高价被买方识破后,市场对卖方所追加的惩罚成本。
⑸而且 Vg>Ph,Vb>Pl,Vl<Ph,否则,产权交易行为不会产生(假定交易双方的卖价、买价等都是在充分考虑了各种可能影响因素的基础上理性做出的)。
⑹买方不能讨价还价,要么接受卖方定价,要么不买。
⑺使用净收益指标来衡量博弈双方的得益。如果交易成功,当知识产权质量高时,若卖方选择定高价,买方和卖方的得益分别为Vg-Ph、Ph-Ch,若卖方选择定低价,买方和卖方的得益分别为Vg-Pl、Pl-Ch;当知识产权质量低时,若卖方选择定高价,买方和卖方的得益分别为Vb-Ph、Ph-Cl-C1,若卖方选择定低价,买方和卖方的得益分别为Vb-Pl、Pl-Cl。如果交易失败,若卖方的知识产权质量低,定高价将有损失C=-Cl-C1-C2,定低价将有损失-Cl,若卖方的知识产权质量高,定高价和低价都损失-Ch,卖方不购买的得益均为0。
⑻为简化分析,假设 Vg-Ph>Vb-Pl>0>Vb-Ph,即用高价购买质量高的知识产权比用低价购买质量低的知识产权收益大;而低价购买一个质量低的知识产权还不至于取得负的收益。如果买方用高价购买质量低的知识产权就可能会取得负的收益;买方用低价购买质量高的知识产权的收益是最高的,这时可能存在知识产权价值被市场低估或存在某些关联交易、利益输送的可能性[2]。
根据上述假设,买方购买知识产权的期望收益为:

公式中的四个概率依次为定价高的知识产权质量高、定价高的知识产权质量低、定价低的知识产权质量高、定价低的知识产权质量低的条件概率。显然,当E(V)≥0时,买方选择购买;当E(V)<0时,买方放弃购买。
2.2 知识产权交易的博弈过程分析
考虑到交易双方信息的不对称和双方交替决策的动态过程,可以这样思考该博弈问题:
第一阶段,自然n选择知识产权的类型,为了简便起见,我们假设卖方知识产权的类型只有质量高、低两种情况,卖方知识产权类型集以θ={g,b}表示,其中g代表卖方知识产权质量高,b代表卖方知识产权质量低,假设知识产权质量高的先验概率用p(g)表示,知识产权质量低的先验概率用p(b)表示,且满足:p(g)+p(b)=1,其中:
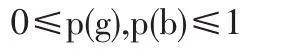
第二阶段,卖方根据自然n的选择,选择定价p作为信号,信号空间为 P={Ph,Pl},其中 Ph为定高价,Pl为低定价,Ph>Pl。
第三阶段,买方不知道知识产权的类型θ,只知道知识产权属于θ的概率分布p(θ),当卖方向买方发出信号p时,买方根据卖方发出的信号(定价P),应用贝叶斯法则修正先验概率,并得到关于知识产权质量高或低的后验概率p(θ/P),然后根据p(θ/P)从行动集以A={a1,a2}选择一个行动,决定买或不买,其中a1表示买,a2表示不买。
上述博弈过程用博弈树表示就是如下的扩展式:
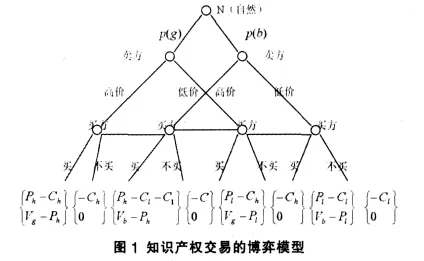
图1终点括号内的上面的数字为卖方的得益,下面数字为买方的得益。一般情况下,由于卖方在知识产权质量高、低两种情况下都有选择定高价和低价的可能性,因此买方不能根据卖方出价的高低而简单地判断知识产权的质量,他还要进行其他信息的搜集与分析。因此买方必须根据卖方的定价和自己过去的经验,参考同类型知识产权的交易价格并且利用贝叶斯法则正确判断卖方知识产权的质量高低。
不难看出,信号传递博弈实际上是不完全信息情况下的斯坦克尔伯格(Stackelberg)博弈(信号发送者是领头者(Leader),信号接受者是尾随者(Follewer))[3]。 当参与人 1(卖方)发出信号即价格时,他预测到参与人2(买方)将根据其发出的信号修正对自己类型的判断,因而选择一个最优的类型依存信号战略;同样,参与人2(买方)知道参与人1(卖方)选择的是给定类型和考虑信息效应情况下的最优战略,因此使用贝叶斯法则修正对参与人1(卖方)类型的判断,选择自己的最优行动,即买或不买。
3 知识产权交易定价博弈模型的分析与求解
3.1 对参与人2(买方)的分析
3.1.1 定高价时的分析
在卖方出高价时,买方有买或不买两种选择,但其最终的选择则必然是得益中最大者。根据前述分析,于是有:
买方选择=Max{(P(g/h)(Vg-Ph)+P(b/h)(Vb-Ph)),0}
下面分两种情况进行讨论分析:
①如果买方选择买,则必有:
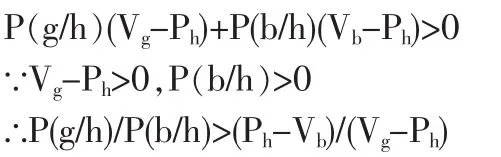
②如果买方选择不买,则必有:
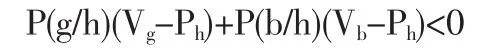
同理,解得:

通过上述综合分析可以得到如下结论:在知识产权交易博弈中,如果卖方定高价,买方选择买的条件是(g/h)/P(b/h)>(Ph-Vb)/(Vg-Ph),选择不买的条件是 P(g/h)/P(b/h)<(Ph-Vb)/(Vg-Ph)
3.1.2 定低价时的分析
在卖方出低价时,买方有买或不买两种选择,但其最终的选择则必然是得益中最大者。根据前述分析,于是有:
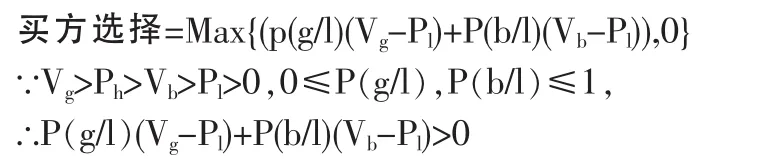
因此,在卖方定低价的情况下,买方的选择都是买。
3.2 对参与人1(卖方)的分析
3.2.1 相关概率假设
笔者为分析方便,假设:
卖方定高价,买方买的概率:

卖方定高价,买方不买的概率:

卖方定低价,买方买的概率:P(a1/l)=1
卖方定低价,买方不买的概率:P(a2/l)=1-P(a1/l)=0
3.2.2 知识产权质量高时的分析
在知识产权质量高时,卖方有定低价或定高价两种选择,但其最终的选择则必然是卖方得益中最大者。根据前述分析,可以得知:
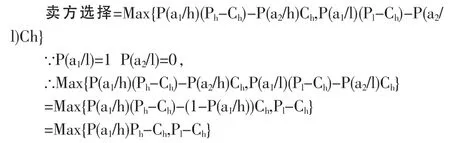
因此,当 P(a1/h)Ph-Ch>PI-Ch,即 P(a1/h)>Pl/Ph时,即卖方在知识产权质量高时定高价;当 P(a1/h)Ph-Ch<Pl-Ch,即 P(a1/h)<Pl/Ph时,卖方在知识产权质量高时定低价。
3.2.3 知识产权质量低时的分析
在知识产权质量高时,卖方有定低价或定高价两种选择,但其最终的选择则必然是得益中最大者。根据前述分析,于是有:
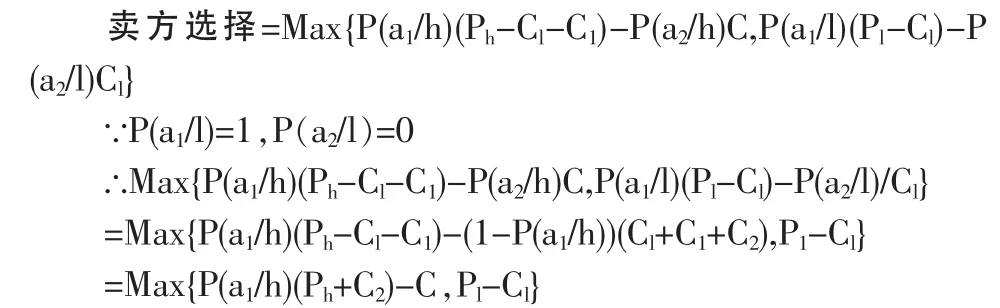
因此,当 P(a1/h)Ph-Ch>Pl-Ch,即 P(a1/h)>Pl/Ph时,即卖方在知识产权质量低时定高价;当 P(a1/h)Ph-Ch<Pl-Ch,即 P(a1/h)<(Pl+C1+C2)/(Ph+C2)时,卖方在知识产权质量低时定低价。
3.3 知识产权交易定价博弈模型求解
3.3.1 买方博弈模型求解
在卖方定高价时,买方以 P(a1/h)=P(g/h)/P(b/h)>(Ph-Vb)/(Vg-Ph)的概率选择购买,以 P(a2/h)=P(g/h)/P(b/h)<(Ph-Vb)/(Vg-Ph)的概率选择不买;在卖方定低价时,卖方选择购买。
3.3.2 卖方博弈模型求解
当买方确定购买时,如果知识产权质量高,买方高价购买的概率P(a1/h)>Pl/Ph时,卖方定高价,在买方高价购买的概率P(a1/h)<Pl/Ph时,卖方定低价(特殊情况);当知识产权质量低时,买方出高价购买的概率P(a1/h)>(Pl+C1+C2)/(Ph+C2)时,卖方定高价,买方出高价购买的概率P(a1/h)<(Pl+C1+C2)/(Ph+C2)时,买方定低价。
3.3.3 重复交易博弈分析
从上述分析可以看出,当交易只进行一次时,无论知识产权质量高低,卖方都存在定高价或低价的可能。但是在现实的知识产权交易市场中,买卖双方的博弈是重复进行的。因此,当某个买方以高价购买了质量较低的知识产权,就会向交易市场反馈卖方定高价的知识产权可能质量低的信息,从而使得后续交易者不断降低自己高价购买P(a1/h),最终迫使卖方无法满足P(a1/h)>(Pl+C1+C2)/(Ph+C2)的条件,从而减少高价销售质量较低知识产权的行为。而在知识产权质量高时,由于信息不对称现象的存在,会存在“劣币驱逐良币”的现象(即质量高的知识产权在定高价时也卖不出去),只能降价出售。如此以往,整个社会的知识产权交易就会步入良性循环的轨道。
4 结论
通过对知识产权交易定价进行了博弈分析,指出独立的一次性知识产权交易博弈中,买卖双方存在五种可能的博弈结果,即(质量高,定高价,购买)、(质量高,定低价,购买)、(质量高,定高价,不购买)、(质量低,定高价,购买)、(质量低,定低价,购买)。在知识产权质量高时,卖方选择定高价或定低价的标准是买方高价购买的概率P(a1/h)是否大于Pl/Ph;在知识产权质量低时,卖方选择定高价或定低价的标准是买方高价购买的概率P(a1/h)是否大于(P1+C1+C2)/(Ph+C2);在重复交易的知识产权市场中 (市场有效),买卖双方只存在两种博弈结果,即(质量高,定高价,购买)、质量低,定低价,购买)。本文的研究结论对于不断加强和完善知识产权交易市场建设,促进知识产权交易良性循环和合理配置具有重要的理论指导意义。
[1]Reilly,R.F.,M.P.Dandekar.Valuation of Intangible Contract Rights[J].The CPA Journal,1997,6.
[2]吴汉东.中国知识产权的国际战略选择与国内战略安排[J].今日中国论坛,2006(Z1).
[3]肖军,刘倩.知识产权的价值向度与制度构建[J].求索,2009,(8).
[4]张维迎.博弈论与信息经济学[M].上海:上海三联书店,上海人民出版社,2004.
[5]王月欣.关于知识产权的定价信号博弈问题[J].理论探索,2008,(4).
[6]陈悦,倪浩,陶柏.企业并购中的讨价还价博弈模型[J].统计与决策,2004,(3).
[7]王义秋,王琳.企业并购定价的博弈分析[J].东北大学学报(自然科学版),2004,(6).
F224
A
1002-6487(2010)22-0060-03
国家自然科学基金资助项目(70972145)
刘卫国(1974-),男,陕西西安人,博士,讲师,研究方向:技术创新管理。
李乾文(1970-),男,河北石家庄人,博士,教授,研究方向:创业管理。
(责任编辑/亦 民)

