空间机器人气浮式物理仿真系统有效性研究*

郑永洁，张笃周,2，谌 颖,2

(1.北京控制工程研究所，北京 100190； 2.空间智能控制技术重点实验室，北京 100190)

空间机器人气浮式物理仿真系统有效性研究*

郑永洁1，张笃周1,2，谌 颖1,2

(1.北京控制工程研究所，北京 100190； 2.空间智能控制技术重点实验室，北京 100190)

针对典型的空间机器人气浮式物理仿真系统，根据实际系统具有的姿态稳定、相对逼近、空间机器人系统协调运动、抓取和释放等工作模式，从基本动力学原理和两系统中分别实际存在的扰动两个层次上，分析了仿真系统对实际系统模拟的有效性，总结了对仿真结果有效性影响最为严重的干扰因素，分析结果为此类仿真系统的有效性检验提供了一种思路和方法.

空间机器人；物理仿真；气浮台

空间机器人技术是一类具有实用价值的航天技术.中国的空间机器人技术还处在研究阶段，面对一个全新的航天工程，必须进行充分的地面试验和验证.迄今为止，国内外学者提出的空间机器人物理仿真方案中，气浮式仿真系统最为可行[1，2].但针对所设计的仿真系统，其有效性的分析研究，还没有进行过系统的讨论，工程研制人员只是依据经验尽量减小各种干扰，来保证仿真结果的可信性.本文针对典型的空间机器人气浮式物理仿真系统，较为全面的分析了系统的有效性问题.

1 空间机器人气浮式仿真系统的一般组成

仿真系统中，由大平台所在平面来模拟实际系统所处的轨道面，由气浮台来模拟空间机器人和空间操作对象，称为模拟星.模拟星在气足的支撑下，与气浮平台间形成约20μm的气膜，保证模拟星在平面上的近似无阻力运动.在模拟星上分别装备实际空间机器人和抓取目标上拥有的控制系统.主要包括：

1)姿态控制系统执行装置：飞轮和反作用喷气系统以及相应的驱动电路盒.

2)姿态测量装置：陀螺和加计以及相应的信号处理电路，相对位置和姿态测量系统.

3)台上数据处理系统：GNC计算机、机械手控制计算机.

4)遥测遥控系统：模拟航天器对地通信装置.

5)台上支持系统：供电、供气系统，调平衡系统等.

6)机械手臂或抓取手柄.

此外，台下支持系统还包括装有仿真软件的PC机，无线接收装置，显示装置，模拟星位置和姿态的监测系统，动力学计算机等.

模拟星具有3个自由度，模拟航天器在轨道面内的平动和绕轨道面法线的转动，在气浮平台上，除了载体之外，为了补偿机械臂所受的重力影响，在机械臂的关节下部也用气足支撑，保证其在水平面内的近似无扰运动，同时不对载体造成力矩干扰.总体结构如图1所示[3-4].

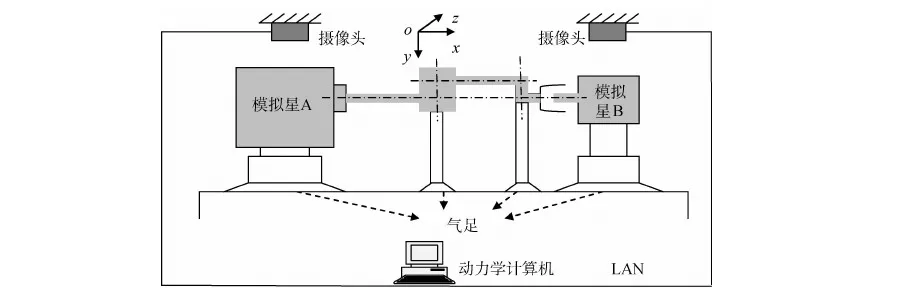
图1 仿真系统总体结构

2 仿真系统的有效性分析

从仿真系统的组成可以看出，三自由度仿真系统用于模拟星体的俯仰姿态运动和轨道面内的位置运动.典型的工作模式为：空间机器人从姿态稳定状态(如三轴对地稳定)开始，逼近目标航天器，进入相对位姿保持，机械臂抓取目标航天器，将其移动到新的位姿后释放，后撤，重新进入稳定状态[3].因此有效的仿真系统应该能够反映出实际系统在轨道面内的运动状态，即轨道面内的姿态稳定、相对位置逼近、机械臂与载体的耦合运动、抓取和释放.鉴于此，对每个典型运动均从两个层次上来进行分析说明仿真系统的有效性：一是在理论状态下，两套系统的动力学应该相同，二是在存在各种不可避免的干扰的情况下，仿真系统与实际系统轨道面内的运动之偏差仍然在可以接受的范围内.

2.1姿态稳定过程的有效性分析

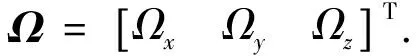
这即是小角度时完整的足够精确的3自由度姿态运动方程，其中ωo表示航天器的轨道角速度.仿真系统中，模拟星被限定只能在气浮平面上运动，因此其姿态动力学方程为：

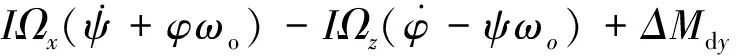
假设在位于275km高度圆轨道的空间机器人系统中，空间机器人本体姿态控制精度和稳定度约为：0.1°和0.01(°)/s，转动惯量阵为diag{450,660,450}kg·m2；初始姿态角和姿态角速度为：

ψ0=θ0=φ0=5°,

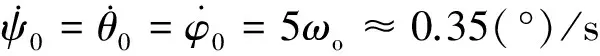
将典型的干扰力矩综合表达为[6]：

而仿真系统中模拟星受到的干扰力矩主要是与转动角速度的方向相反的摩擦力矩，叠加上随机噪声变量w(t)，综合表示为[7]：

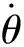
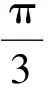
最大俯仰角度偏差、最大俯仰角速度偏差、稳态角度偏差以及稳态角速度偏差分别为：

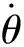
仿真系统对于姿态控制精度约为0.1°，角速度约为0.01(°)/s的实际系统的模拟是有效的.但对更高精度的控制系统仿真而言，必须进一步减小干扰作用.

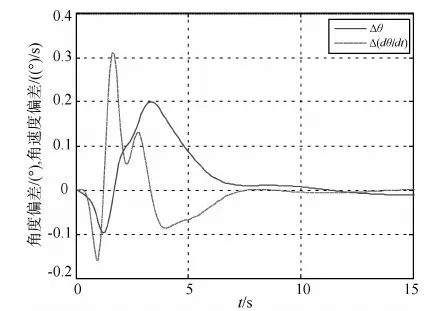
图2 俯仰姿态稳定仿真偏差

2.2逼近运动的有效性分析

在目标航天器上建立Hill坐标系Ohxhyhzh：原点位于目标航天器质心，xhzh平面为目标航天器轨道面；Ohxh轴沿轨道周向，指向运动方向；Ohzh轴与目标航天器矢径重合，但指向地心[8].

以圆轨道为例，对近距离逼近来说，线性化的C-W方程对相对运动的描述非常准确，因此采用Hill系中的线性化相对运动方程来计算实际机器人的运动情况[9]：

以地面为固定的惯性参考系，可得到模拟机器人星在模拟Hill系中的相对运动方程：

ωo表示目标器轨道角速度.ax、ay、az表示投影于相应Hill坐标系的推力加速度.

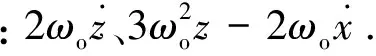
实际系统在逼近过程中，逼近开始时存在位置和姿态确定误差，其中姿态偏差通过姿控系统进行调整，有效性如上讨论.位置方面，则可以比较制导律作用下的位置响应.以直线制导为例[10]，当实际系统初始相对位置和速度误差分别为：

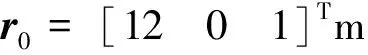
在此基础上迭加仿真系统气浮台摩擦干扰为

此时计算结果如图4所示.

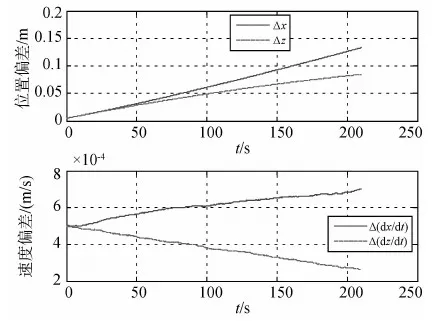
图3 初始导航误差影响下平面相对运动偏差

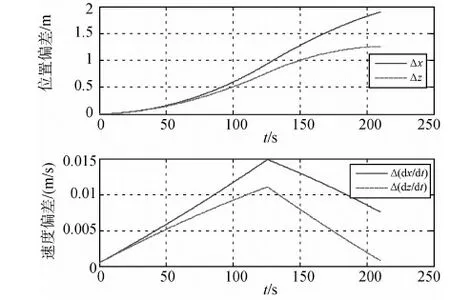
图4 初始导航误差和摩擦干扰同时作用下平面相对运动偏差

可以看出，在摩擦作用下，两系统响应偏差明显增大，位置误差达到Δx=1.8m，Δz=1.2m，这意味着向目标器的逼近是完全失败的.因此气浮轴承的摩擦是一个非常严重的干扰，必须降低.更多的仿真数据表明试验时必须设法将摩擦降至10-5N的量级.

2.3载体、机械臂耦合运动过程的有效性分析

在研究空间机器人机械臂动作的过程时，因为机械臂和载体的运动是耦合的，综合考虑，采用Lagrange方法建立n关节机器人系统的动力学方程[11]:

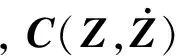
同样的方法可以得到仿真机器人系统的动力学方程与上述方程形式相同，只是自由度变为：载体和机械臂在水平面内的平动和绕铅垂轴y的转动.考察仿真系统与实际系统的差别，可以看出，由于气足的引入，使得仿真系统中连杆的质量和惯量分布，以及广义力发生了变化.关于连杆的质量和惯量分布差别，可以重新配重，即设计仿真系统中连杆加气足总的质量和惯量阵与实际连杆相同.但由于气足底部的摩擦引入的广义力，则无法彻底消除，必须检验其对仿真系统的影响.记仿真系统中的n+3维广义力向量为F′，则：

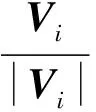
以二连杆空间机器人在轨道面内运动的仿真有效性为例进行数值分析.气足所受扰动力用典型的静摩擦+Coulomb+黏性+Stribeck摩擦模型来表示，即：

Fdi=

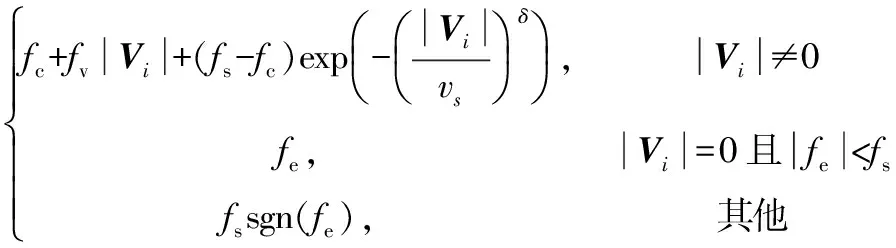
其中： stribeck速度vs取10-3m/s，经验常数δ取2，黏性摩擦系数fv取10-3，库伦摩擦fc取10-3N，最大静摩擦fs取8×10-3N.其它固定参数采用前述载体参数.不控状态下，初值为：

此时几个广义坐标的运动情况如图5所示.

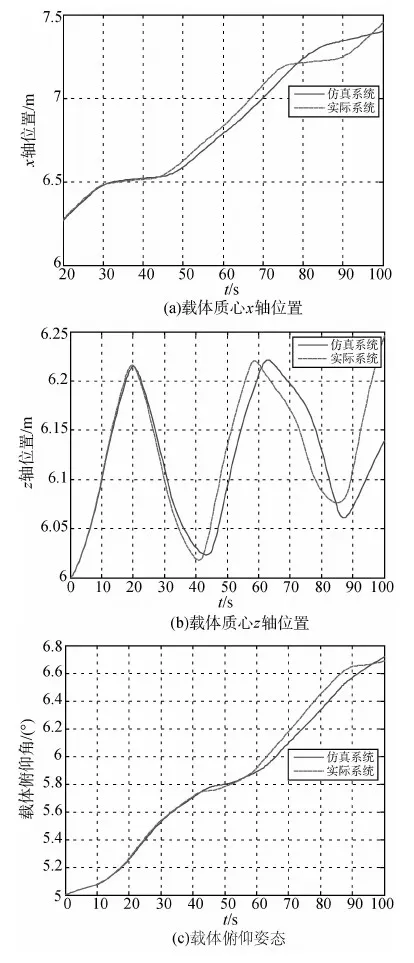
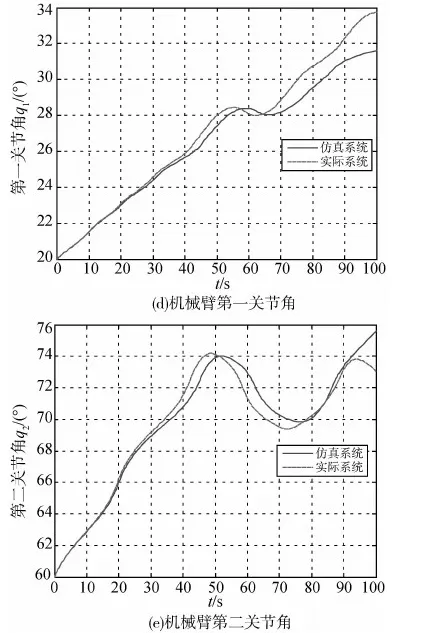
图5 气足干扰引入后实际机器人系统与仿真系统的运动偏差

可以看出两系统差别迅速增大，干扰作用对仿真系统有效性影响不容忽视.

2.4抓取、释放过程的有效性分析

抓取和释放时，由于手抓与抓环的接触，有相互碰撞产生.记p0、H0为机器人星受到的动量和动量矩干扰在本体系下的投影，它们可由机械爪的实验数据得到，从而可以计算出两颗星受扰后各自的姿态、轨道运动和相对运动情况.实际系统在抓取和释放瞬间产生的扰动是轨道面内和轨道面外同时存在的，而仿真系统只能表现出轨道面内的干扰.而实际系统中，相对运动在三个轴上是耦合的，因此需要比较两套系统轨道面内的响应的差别.姿态运动可单独考虑.另一方面，对轨道面内的扰动，由于释放完成后，各自姿轨控系统的启动需要一定时间，因此必须清楚在控制系统再次工作之前，扰动对两星带来的运动量有多大，确保气浮台的面积可以进行全过程模拟.

相对运动方面，释放时，追踪星受到的相对速度扰动在Hill系中可表示为：

m1=800kg,m2=100kg表示追踪星和目标星的质量.计算曲线如图6所示.

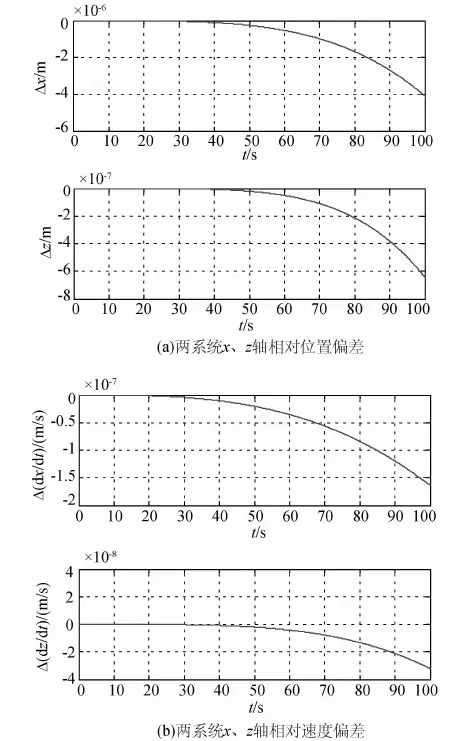
图6 碰撞后系统平面相对位置和相对速度偏差

由仿真曲线看出，模拟追踪星在气浮平面的相对运动与实际航天器轨道面的相对运动偏差很小，位置和速度分别在10-6m和10-7m/s的量级.

2.5气浮台平面运动的仿真有效性分析

前述讨论表明在小角度情况下，在姿态稳定过程、逼近过程和机械臂动作过程中，模拟星在气浮平面的运动能够较为可信的反应实际航天器在轨道面内的运动.但这样的有效性是建立在一定假设条件下的，即：模拟星所受到的合外力严格位于气浮平面内，所受到的合外力矩严格垂直于气浮平面.为此，需要详细考察实验系统中模拟星所受的平面外的力和平面内的力矩.

分析可知，气浮平面内的干扰力矩来源主要有：1)、载体质心偏移气足支撑中心，2)、机械臂的支撑高度与载体的支撑高度不一致，3)、机械臂的安装点与载体质心的连线不平行于气浮平面，4)、机械臂的关节轴不垂直于气浮平面，5)、反作用发动机的推力不经过质心，且有不垂直于气浮平面的力矩产生.当这些干扰力矩都位于同一方向时，构成最大干扰力矩：Md=Md1+…+Md5.这种力矩的作用将造成模拟星倾斜，一侧气足厚度减小，气足产生的支撑力增大，重新使得模拟星受力矩平衡.

静止状态下y轴上受到的重力和气足的支撑力是相等的，合力为零，这里所谓的干扰力不包括它们.干扰力来源主要有：1)、机械臂的安装不平行于气浮平面，2)、反作用发动机的推力不平行于气浮平面.总干扰力为两者之和：Fd=Fd1+Fd2.

当模拟星所受平面内的力矩使得台体向某一个气足一侧倾斜，同时，由于垂直方向上的压力变化也叠加在这个气足上时，这个气足将承受最大的压力变化范围，如图7所示.

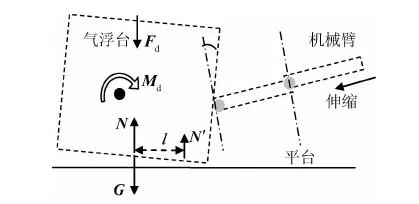
图7 模拟星力、力矩平衡示意图

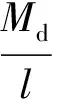
3 结 论

本文从空间机器人的任务特点出发，将空间机器人的工作模式详细分类，从姿态稳定过程、逼近过程、机械臂动作以及抓取和释放过程，分析了空间机器人气浮式物理仿真系统对实际系统模拟的有效性.分析表明，仿真系统必须满足模拟星所受合外力严格位于气浮平面内，所受合外力矩严格垂直于气浮平面，在此前提下有以下结论：

1)机械臂动作过程中，模拟星在气浮平面的运动可以有效地反映实际航天器在轨道面内的运动趋势；

2)姿态稳定过程和相对逼近过程中，只要初始姿态和位置误差在一定范围内，模拟星在气浮平面的运动能够有效地反映实际航天器在轨道面内的运动趋势.

3)仿真结果的可信度取决于模拟星在气浮平面上运动时所受到的平面内的干扰作用，即气足摩擦作用的大小.进行高精度的物理仿真试验时，必须设法测量出摩擦作用的量值，进行数据上或硬件上的补偿.

[1] 吴立成，孙富春，孙增圻,等. 空间机器人建模、规划与控制研究现状[J]. 中南大学学报，2005，36(1)：18-24

[2] 徐文福，梁斌，李成,等. 空间机器人微重力模拟实验系统研究综述[J]. 机器人，2009，31(1)：88-96

[3] 郑永洁，张笃周，谌颖. 空间机器人物理仿真研究[C]. 全国第十四届空间及运动体控制技术学术会议，四川，2010年7月

[4] Gary L C. Development and control of robotic arms for the naval postgraduate school planar autonomous docking simulator(NPADS)[D]. U.S. Naval Postgraduate School, December 2002

[5] 周军. 航天器控制原理[M]. 西安：西北工业大学出版社，2001，119-122

[6] 屠善澄. 卫星姿态动力学与控制[M]. 北京：宇航出版社，1999，49-65

[7] 李季苏，牟小刚，张锦江，等. 气浮台在卫星控制系统仿真中的应用[J]. 航天控制，2008，26(5)：64-68

[8] 朱仁璋. 航天器交会对接技术[M]. 北京：国防工业出版社，2007

[9] 林来兴，车汝才. 航天器编队飞行动力学模型和精度分析[J]. 航天器工程，2008，17(2)：19-25

[10] 张万里，马广程，温奇咏，等. 交会对接最终逼近段制导控制律设计方法研究[J]. 宇航学报，2007，28(4)：860-864

[11] 张翼. 空间机器人系统的运动动力学及其控制[D]. 国防科技大学，2000

ResearchonCredibilityofAir-BearingTable-BasedPhysicalSimulationSystemforSpaceRobot

ZHENG Yongjie1, ZHANG Duzhou1,2, CHEN Ying1,2

(1.BeijingInstituteofControlEngineering,Beijing100190，China; 2.ScienceandTechnologyonSpaceIntelligentControlLaboratory,Beijing100190，China)

On the basis of different operating modes of real system such as attitude stability, relative proximity, coordinated motion of space robot, capture and release and so on, the paper analyzes the credibility of a air-bearing table based typical physical simulation system for space robot from both basic dynamic equation and various disturbances existed in the two similar systems, and then several important disturbance factors affecting the credibility of simulation system are summarized. Analyze results provides a reference ideal and approach for credibility of similar simulation systems.

space robot; physical simulation system; air-bearing table

V448

A

1674-1579(2010)06-0033-06

*国家自然科学基金( 10872028)资助项目.

2010-09-10

郑永洁(1985—)，男，四川人，硕士研究生，研究方向为航天器系统测试与仿真技术 (e-mail: zyjfl1985@sohu.com).