慢旋非合作目标接近轨迹规划

刘智勇，何英姿

(1.北京控制工程研究所，北京 100190；2.空间智能控制技术重点实验室，北京 100190)

慢旋非合作目标接近轨迹规划

刘智勇1,2，何英姿1,2

(1.北京控制工程研究所，北京 100190；2.空间智能控制技术重点实验室，北京 100190)

非合作目标自主在轨服务是在轨服务领域的研究方向，具备避碰能力的接近轨迹规划将在未来的在轨服务任务中扮演重要的角色.给出了一种基于滚动时域的慢旋非合作目标接近轨迹规划方法，利用逻辑变量和连续变量的混合形式来描述避碰约束，从而将轨迹规划问题转化为混合整数规划问题.仿真结果表明，基于滚动时域设计的慢旋非合作目标接近轨迹规划能够使得在轨服务航天器安全地接近终端状态.

在轨服务; 慢旋非合作目标; 滚动时域; 接近轨道

早在20世纪70年代就有人提出了在轨服务型航天器(OOSS，on-orbit servicing spacecraft)的概念，即专门为其他航天器提供在轨燃料补给、仪器设备维修与升级更换服务、轨道与姿态重置等一类机动性较强的航天器.目前，在轨服务已经从概念转化为现实，例如美国利用航天飞机成功地实现了对哈勃望远镜在轨维修，这些实践让人们看到了在轨服务在航天技术发展中所具有的重大意义.未来在轨服务任务的对象航天器很多情况下将是非合作目标，研制具备非合作目标在轨服务能力的航天器是目前在轨服务领域的研究方向，各主要航天大国均积极开展了相关研究和在轨试验，如通用轨道修正航天器(SUMO)[1-2]，轨道延寿飞行器(OLEV)[3-4]等.

大部分失控和被废弃卫星处于缓慢翻滚状态，随着能量的耗散最终将绕最大惯量轴慢旋，并且自旋轴的指向任意.为了使得机械臂能够顺利抓捕旋转目标，在轨服务航天器需要保持与旋转目标上抓捕点的相对位置不变，即相对位置在旋转目标的本体坐标系下的表示为常量.在轨服务航天器抓捕慢旋非合作目标，如图1所示.

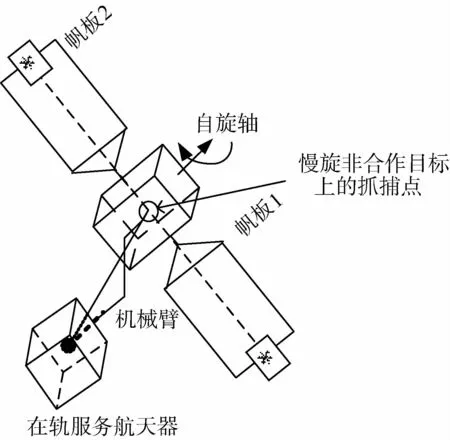
图1 在轨服务航天器抓捕慢旋非合作目标

由于非合作目标的慢旋运动，在轨服务航天器的终端状态在惯性空间下的表示为绕自旋轴的空间时变轨线.并且，非合作目标的旋转运动，使得在轨服务航天器在接近的过程中，极有可能与非合作目标发生碰撞.这些都导致慢旋非合作目标的接近轨迹规划的难度很大.

目前，国内外对空间交会问题的研究，主要是针对三轴稳定目标的，常用的交会方式有V-bar交会[5]、R-bar交会[6]、Glide-slope接近[7]等.由于本文研究的非合作是慢旋的，并且指向任意，使得以上接近方式不再适用，需要研究新的接近算法.

本文针对慢旋非合作目标的接近轨迹规划问题进行了研究，首先，建立了惯性坐标系下的相对位置运动动力学模型，描述了末端状态的运动形式，系统的各类约束；然后，将问题转化为基于滚动约束的非线性规划问题.仿真结果表明，在轨服务航天器基于滚动时域设计的慢旋非合作目标接近轨迹规划能够安全地到达终端状态.

1 慢旋非合作目标自主接近问题描述

针对图1所示的翻滚目标的接近问题，讨论在轨服务航天器从初始状态出发，在一定的优化指标下到达终端状态，同时满足状态约束和避免撞到障碍物.

1.1相对位置动力学模型

在惯性坐标系下，慢旋非合作目标和在轨服务航天器的轨道动力学方程为

式中，μ为地球引力常数，rti，rci为慢旋非合作目标和在轨服务航天器的地心距矢量，ati，aci分别为慢旋非合作目标和在轨服务航天器在摄动力(包括地球形状摄动、大气阻力摄动和光压摄动等)作用下的摄动加速度矢量，aJi为在轨服务航天器在推力器作用下的加速度矢量.令

其中，ρi为在轨服务航天器相对于慢旋非合作目标的相对位置在惯性坐标系下的表示.

从而可得

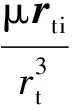
由于

并且

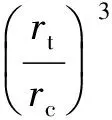
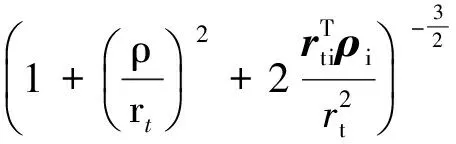
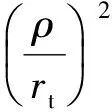
从而

航天器正常的运行当轨道高度在120km以上，所以rt>6498km.由式(8)可以看出，在近距离aei(j)为10-4m/s2量级 (j=1,2,3).而摄动加速度之差adi更小，不失一般性，可以将aei+adi视为过程干扰.

为了便于分析，将相对运动动力学模型写成状态空间的形式

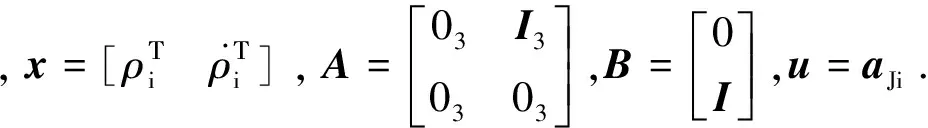
离散时间形式的状态空间模型为

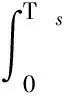
在预测步长为H的条件下，利用迭代模型式(10)来进行预测，可得

1.2末端抓捕位置描述

利用姿态四元数描述航天器的姿态，由欧拉转角φ和欧拉转轴e组成，如下式

其中，q为姿态四元数，分为矢量部分qv和标量部分q4.坐标转换矩阵C可以通过定义的姿态四元数计算

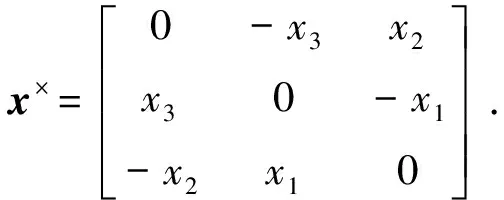
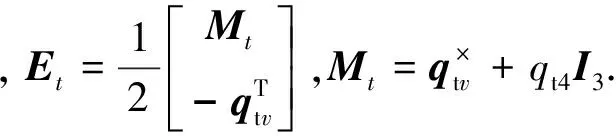
非合作目标的姿态动力学为

其中，τ为作用在非合作目标上的力矩，由于非合作目标在空间翻滚，没有控制力矩的作用，从而只有环境力矩作用在非合作目标上面，并且力矩的值很小，短时间内对姿态的影响可以忽略.

假定目标上面的抓捕点在目标本体坐标系中坐标为Xgb，那么在目标轨道坐标系下表示的在轨服务航天器末端抓捕位置为

速度为

由以上讨论可知，接近轨迹的终端状态决定于翻滚非合作目标的姿态和目标本体系下选定的位置，并且在惯性坐标下的表示为时变量.

1.3动态约束

假定在轨服务航天器和非合作目标的初始状态为x0，相对运动速度和控制加速度的约束分别为

1.4避障约束

任意形状的障碍物可以用多面体近似，避碰约束可以通过引入逻辑变量和“big-M”的方法，表示为逻辑变量和连续变量的混合决策变量的线性约束.非合作目标的外形为中心刚体加太阳帆板，如图一所示.考虑到在轨服务航天器的厚度，需要将非合作目标为中心的避碰区域适当的放大.所以，在目标本体坐标系下，慢旋非合作目标为中心的避碰区域选择为一长方体，如图2所示.

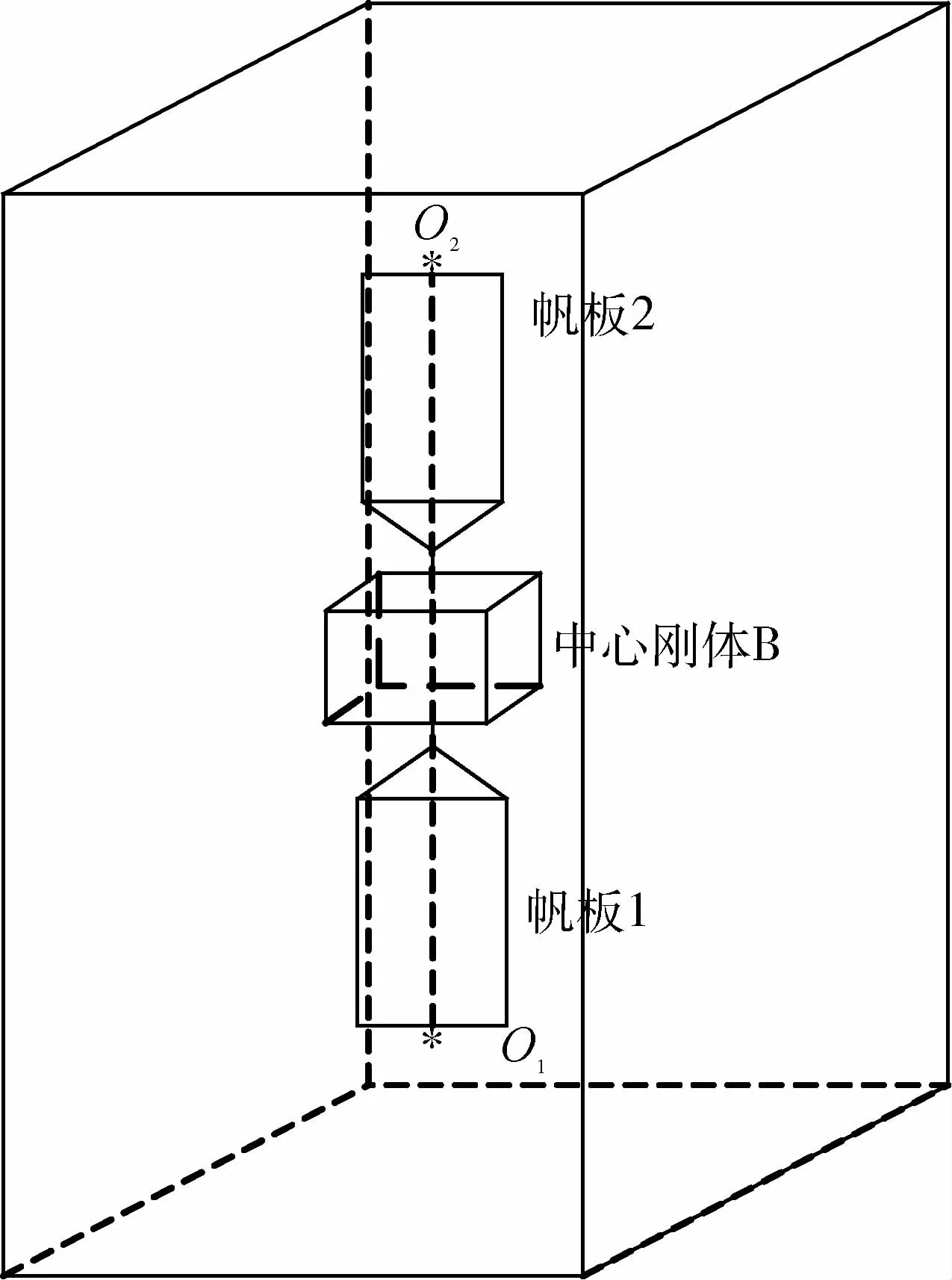
图2 慢旋非合作目标的避碰约束

从而，避碰区域可以表示为

通过引入逻辑变量和“big-M”的方法，将避碰约束表示为逻辑变量和连续变量的混合决策变量的线性约束，避碰约束可以表示为：

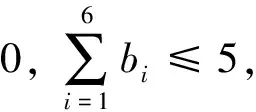
2 基于滚动时域的接近轨迹规划

基于以上讨论，可以建立慢旋非合作目标的自主接近轨迹规划问题，并采用滚动时域策略，取有限时域优化指标为

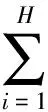
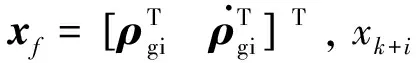
可以看出此问题实际上为一个混合整数规划问题，设在当前离散时刻k，求解此混合整数规划问题得到有限时域最优控制序列{uk,…,uk+H-1}和状态序列{xk+1,…,xk+H}.根据滚动时域控制的思想，当前时刻k实际作用到系统得控制信号仅为第一个控制信号uk，其他控制信号实际上并没有作用到系统中.在下一个时刻k+1，当xk+1测量得到时，再次求解混合整数规划问题得到有限时域最优控制序列为{uk+1,…,uk+H}，同样只用第一个控制信号uk+1到系统中.反复以上过程，最优轨迹序列为x0,x1,…,xk-1,xk,…,xf.

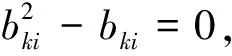
3 仿真算例与分析

非合作目标的轨道参数为：半长轴at=7040 km，偏心率et=0.001，轨道倾角it=97.4°，近地点幅角ωt=90°，升交点赤经Ωt=0，且卫星经过近地点的时刻tp=0.

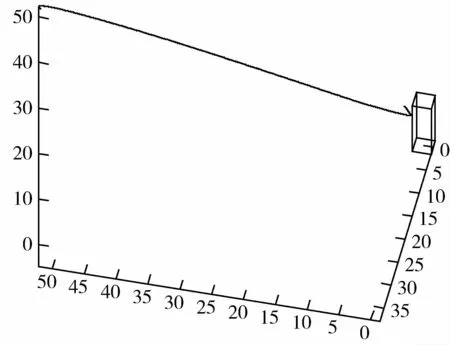
图3 接近轨迹在目标本体坐标系下的表示

从图3中可以看出，本文规划出来的轨线能够从选定的初始位置，到达抓捕点的上方，并且在接近的过程中没有进入避碰区域，保证了安全性.

从图4和图5中可以看出，本文规划的相对位置和相对速度收敛到了期望相对位置和期望相对速度，满足非合作目标抓捕的需求.

由图6可以看出，本文的制导加速度满足规定的加速度约束.

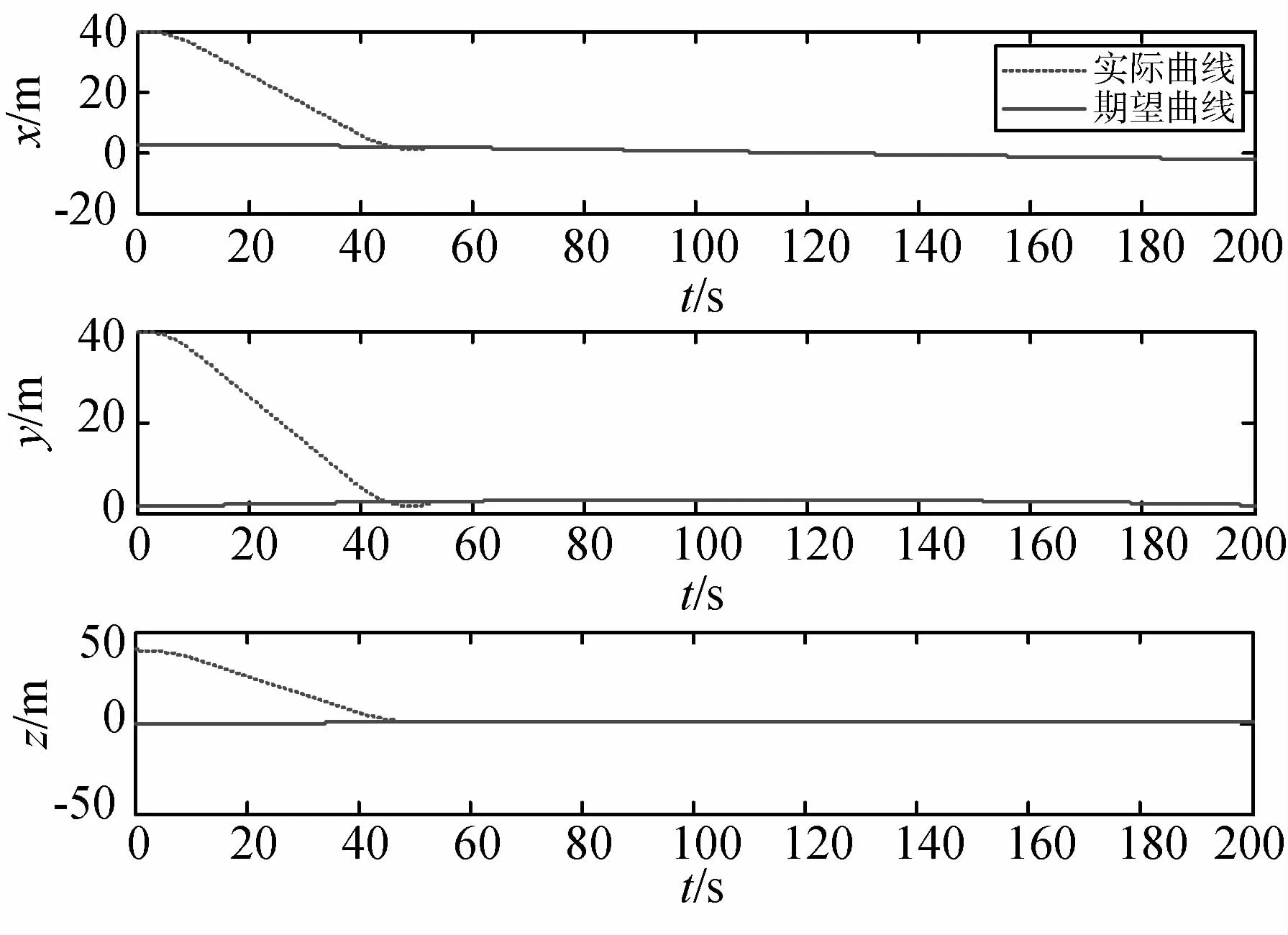
图4 相对位置曲线在惯性系下的表示

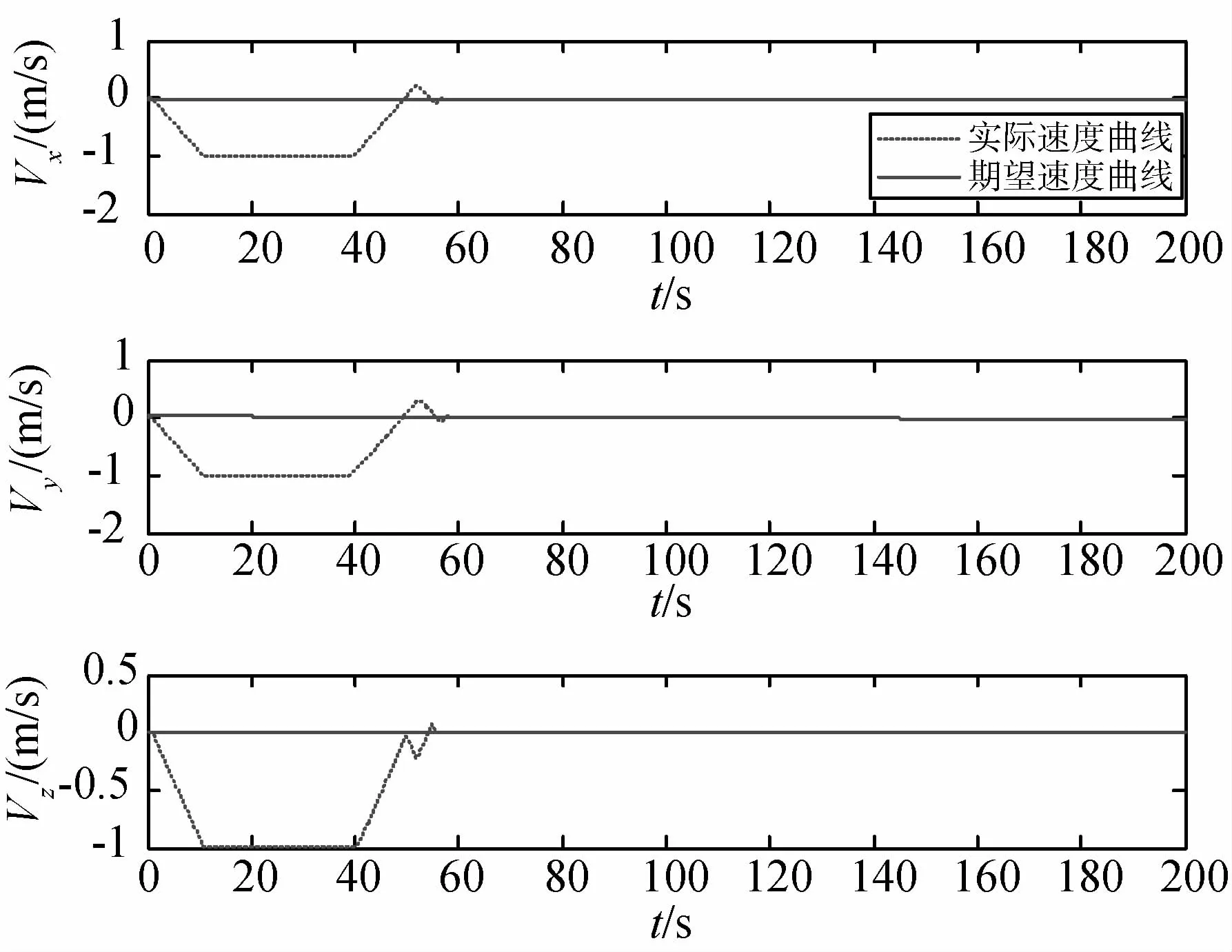
图5 相对速度在惯性系下的表示

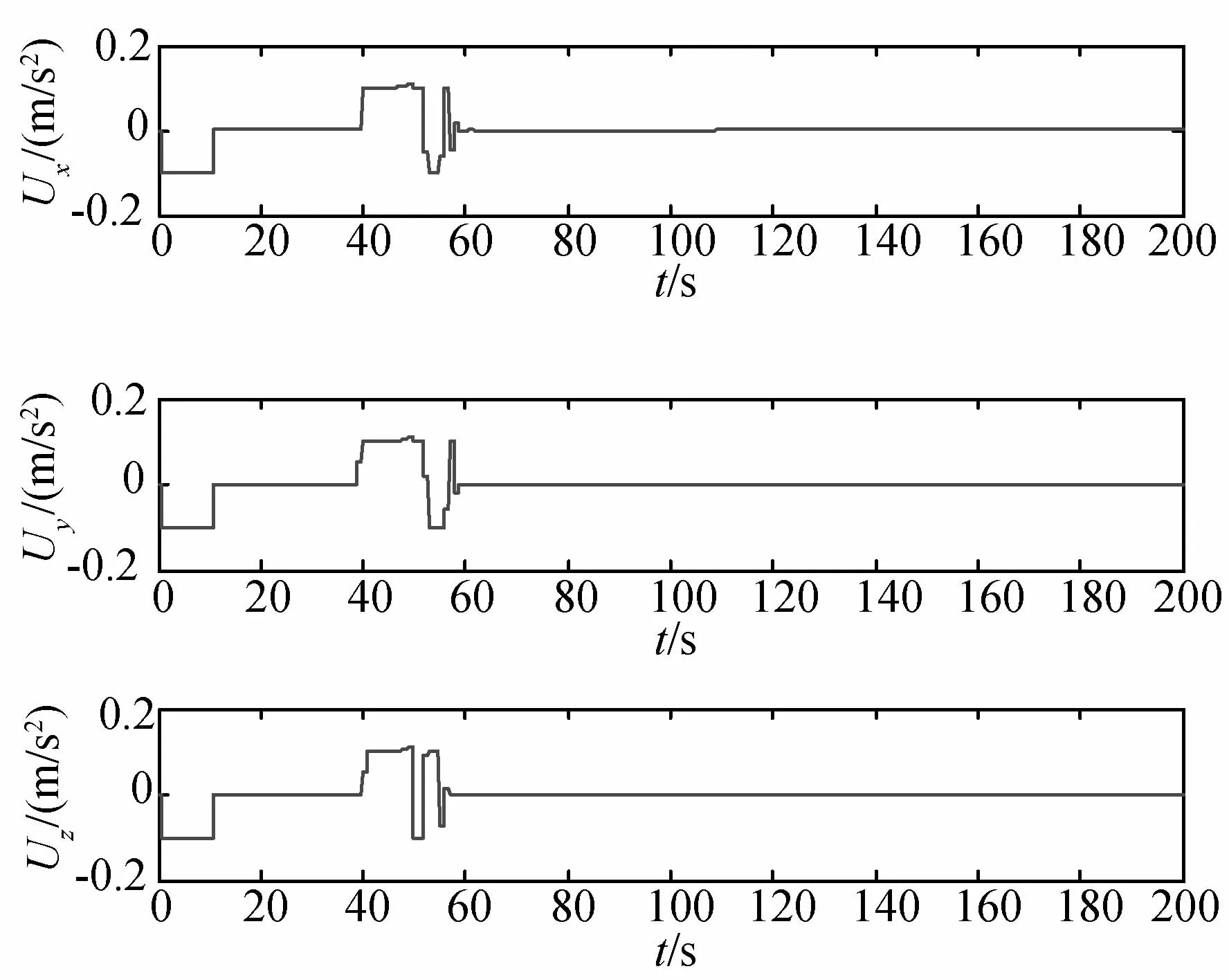
图6 制导加速度曲线

4 结 论

对于终端状态和避碰约束时变的慢旋非合作目标的接近轨迹规划问题，基于滚动时域的思想 ，将其转化含非线性约束的非线性规划问题.仿真结果表明，本文基于滚动时域设计的慢旋非合作目标接近轨迹能够到达所要求的终端状态，并且具有自主调整的能力，保证了安全性.

[1] Albert B, James W, Michael A, et al. SUMO: spacecraft for the universal modification of orbits[C]. Spacecraft Platforms and Infrastructure, SPIE Paper Number 5419-07, Bellingham, WA, Aug 2004

[2] Obermark J, Creamer G, Bernard E, William W, et al. SUMO/FREND: vision system for autonomous satellite grapple[C]. Sensors and Systems for Space Applications, SPIE Paper Number 6555-27, Bellingham, WA, April 2007

[3] Tarabini L, Gil J, Gandia F, et al. Ground guided CX-OLEV rendezvous with uncooperative geostationary satellite[J]. Acta Astronautica ，2007，61 (4) ：312-325.

[4] Kaiser C, Sjoberg F, Dlecura J M, et al. SMART-OLEV: an orbit life extension vehicle for servicing commercial spacecrafts in GEO[J]. Acta Astronautica，2008，63 (4) ：400-410

[5] 杨乐平, 朱彦伟, 安雪滢. 基于组合机动的空间V-bar交会策略[J].国防科技大学学报, 2006, 28(5):6-10

[6] Yamanaka K, Yokota K, Yamada K, et al. Guidance and navigation system design of R-bar approach for rendezvous and docking[C]. International Communications Satellite Systems Conference and Exhibit. Yokohama, Japan, Feb 1998

[7] Hari B H, Tapper M, David D B. Guidance algorithms for autonomous rendezvous of spacecraft with a target vehicle in circular in circular orbit[C]. AIAA guidance, navigation and control conference and exhibit. Montreal, Canada, Aug 2001

SlowlyRotatingNon-cooperativeTargetProximityTrajectoryplanning

LIU Zhiyong1,2, HE Yingzi1,2

(1.BeijingInstituteofControlEngineering,Beijing100190,China; 2.ScienceandTechnologyonSpaceIntelligentControlLaboratioy,Beijing100190,China)

On-Orbit Autonomous Servicing (OOAS) for a non-cooperative target is an important subject in the fields of On-Orbit Autonomous Servicing, and proximity trajectory planning with obstacle avoidance will play an important role in the On-Orbit Autonomous Servicing in the future. A slowly rotating non-cooperative target proximity trajectory planning based on receding horizon is introduce in the paper, and the trajectory planning problem is transformed in to a mixed-integer planning problem described by the mixed form with logic variables and continuous variables. The simulation results demonstrate that the on-orbit servicing spacecraft can securely near the slowly rotating non-cooperative target with by using designed the proximity trajectory.

On-Orbit autonomous servicing; slowly rotating non-cooperative target; receding horizon; proximity trajectory

V448.2

A

1674-1579(2010)06-0006-05

2010-05-10

刘智勇(1984—) 男，江西人，硕士研究生，研究方向为航天器姿态轨道控制 (e-mail: liuzy502@163.com).